Розділ 2. Інтерполяція функцій

§1. Задача інтерполювання

Означення 1. Задачею інтерполяції (або інтерполювання) є побудова такої функції, яка для даних значень аргументу приймає задані значення. Нехай для значень аргументу х₁ , х₂ , … , х_n , які називають вузлами інтерполяції, відомі значення деякої функції f(x): f(x₀) = у₀, f(x₁) = у₁, … , f(x_n) = у_n. Треба знайти інтерполюючу функцію Р(х), так, щоби у вузлах інтерполяції вона приймала ті ж самі значення, що й f(x), тобто Р(x₀) = у₀, Р(x₁) = у₁, … , Р(x_n) = у_n.

Геометрично інтерполювання означає, що треба знайти криву Р(х), яка проходить через задані точки (х₁;у₁), (х₂;у₂), (х₃;у₃), … на графіку функції f(x).

у P(x)

у₄ f(x)

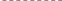
у₃

у ₅ = у₆

у₂

у₁

х

О х₁ х₂ х₃ х₄ х₅ х₆

Рисунок 1

Означення 2. Наближену рівність f(x) ≈ Р_n(х) називають інтерполяційною формулою. Різницю R_n(f,x) = f(x) – Р_n(х) називають залишковим членом інтерполяційної формули або похибкою інтерполювання.

Серед методів інтерполювання найбільш розповсюдженим є лінійна інтерполяція, коли наближення шукають у вигляді Р_n(х; а₀, а₁, … , а_n) = , де φ_i(х) – деякі фіксовані функції, коефіцієнти а_i шукають з умови збіжності значень наближаємої і інтерполюючої функцій у вузлах інтерполяції: f(x_j) = (j = 0,1,…,n). Найчастіше Р_n – многочлен, φ_i(х) = хⁱ (i = 0,1,…,n), Р_n = , а відповідна система лінійних рівнянь має вигляд:

а₀ + а₁х₀ + а₂ +… + а_n = y₀

а₀ + а₁х₁ + а₂ +… + а_n = y₁

. . . . . . . . . . . . . . . . . . . . . . (1)

а₀ + а₁х_n + а₂ +… + а_n = y_n .

Визначник цієї системи лінійних рівнянь

є визначником Вандермонда і оскільки всі вузли інтерполяції х₁ , х₂ , … , х_n різні, то він не дорівнює нулю. Тому система лінійних рівнянь (1) завжди має єдиний розв’язок. Отже, єдиний розв’язок завжди має задача інтерполювання многочленом (1).

Многочлен Р_n(х), який задовольняє умови Р_n(х_i) = y_i = f(x_i) (i = 0,1,…,n) називають інтерполяційним многочленом.