§7 Приклади

Було б помилкою думати, що Поиск решения завжди дає остаточну відповідь на будь – яку задачу лінійного програмування. Розглянемо, наприклад, таку математичну модель

f = 3x₂ + x₁ (max)

.

Складемо відповідну електронну таблицю так, як у першому прикладі цього параграфу:

	A	B	C	D
1	х1	х2	b
2	2	6	10	=СУММПРОИЗВ(A1:B1;$A$5:$B$5)
3	3	2	8	↓
4	1	3	f=	↓
5	1	1

Дістанемо

	A	B	C	D
1	х1	х2	b
2	2	6	10	8
3	3	2	8	5
4	1	3	f=	4
5	1	1

Виділимо цільову чарунку D4 і оберемо Поиск решения у меню Сервис. Всю решту даних математичної моделі заносимо далі у це вікно. А саме після слова Равной: обираємо варіант максимальному значению, у поле Изменяя ячейки вносимо адресу змінних А5:В5.

У полі Ограничения (як і раніше, через вікно діалогу Добавление ограничений) виписана система обмежень цієї задачі: нерівності 2х₁ + 6х₂ ≤ 10, 3х₁ + 2х₂ ≤ 8 у рядку 2, умова невід’ємності змінних у рядку 1.

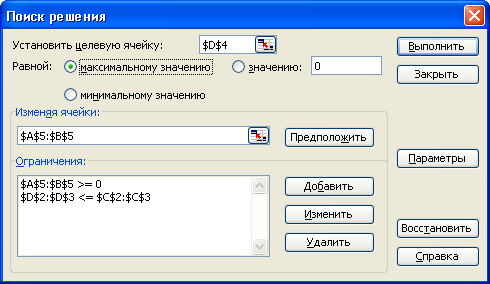
Натиснемо на Выполнить. Дістанемо:

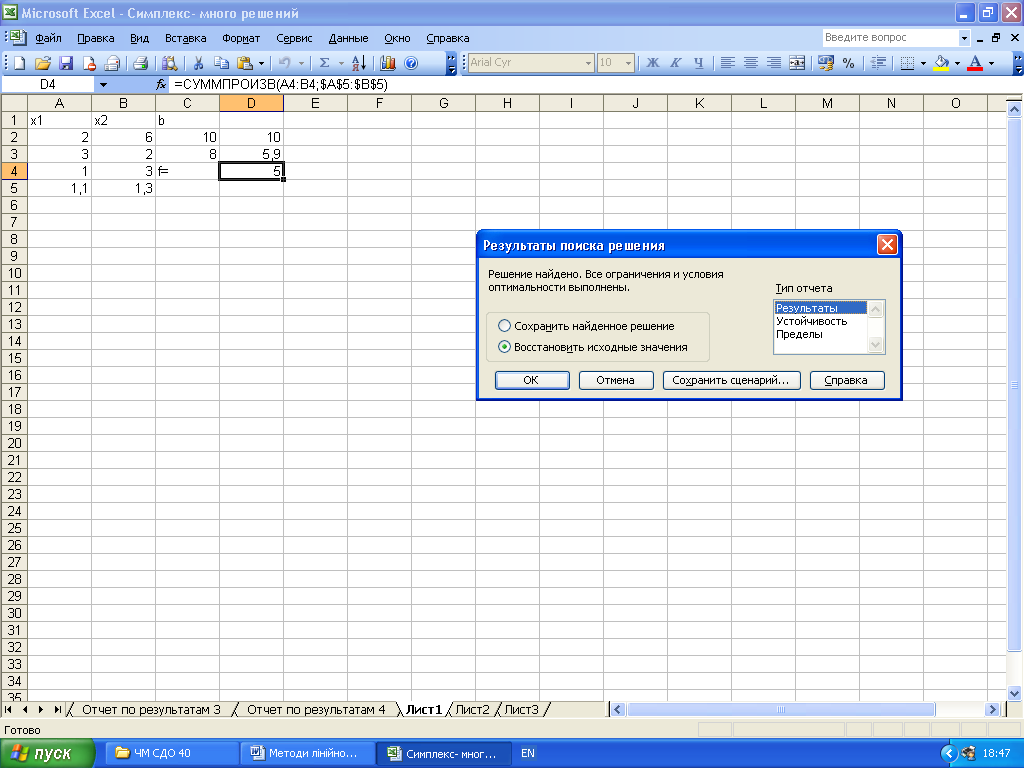
Оберемо Восстановить исходное значение і Результаты у полі Тип отчёта у вікні Результаты поиска решения . Натиснувши на ОК, дістанемо відповідь, яку побачимо, якщо натиснути на Отчёт по результатам 1.

Microsoft Excel 11.0 Отчет по результатам
Рабочий лист: [Симплекс- много решений.xls]Лист1
Отчет создан: 07.02.2010 18:49:49
Целевая ячейка (Максимум)
	Ячейка	Имя	Исходное значение	Результат
	$D$4	f=	4	5
Изменяемые ячейки
	Ячейка	Имя	Исходное значение	Результат
	$A$5	х1	1	1,1
	$B$5	х2	1	1,3

Ніби – то все гаразд, але спробуємо розв’язати ту саму модель з іншими початковими значеннями змінних х₁ = 1, х₂ = 2. Відповідна електронна таблиця:

	A	B	C	D
1	х1	х2	b
2	2	6	10	14
3	3	2	8	7
4	1	3	f=	7
5	1	2

Виділимо цільову чарунку D4, оберемо Поиск решения у меню Сервис, всю решту даних математичної моделі заносимо далі у це вікно так само, як і раніше. Натиснемо на Выполнить і дістанемо:

Натиснувши на ОК, а потім на Отчёт по результатам 2, дістанемо відповідь:

Microsoft Excel 11.0 Отчет по результатам
Рабочий лист: [Книга1]Лист1
Отчет создан: 07.02.2010 15:45:25
Целевая ячейка (Максимум)
	Ячейка	Имя	Исходное значение	Результат
	$D$3	f=	7	5
Изменяемые ячейки
	Ячейка	Имя	Исходное значение	Результат
	$A$4	х1	1	0,8
	$B$4	х2	2	1,4

Перший раз ми дістали х₁ = 1,1 , х₂ = 1,3. Виявляється, що оптимальний розв’язок, який видає Поиск решения, залежить від початкових даних. Чи можливо таке насправді і як це збігається з теоремами, отриманими раніше? Розв’яжемо цю модель симплекс – методом.

1. Зведемо цю задачу до канонічної форми. Ввівши додаткові змінні х₃, х₄, отримуємо:

f = 3x₂ + x₁ (max)

.

Запишемо її у електронну симплекс – таблицю:

	A	B	C	D	E	F
1	x1	x2	x3	x4	b	b/aij
2	2	6	1	0	10
3	3	2	0	1	8
4	1	3	0	0	0

2. Симплекс – таблиця виявляється приведеною до базису А₃ , А₄ опорного розв’язку. Це видно з того, що матриця такого розв’язку на стовпцях змінних х₃ , х₄ є діагональною, а оцінки основних змінних дорівнюють нулю.

3. Серед оцінок базису є додатні, тож згідно з ознакою оптимальності треба виконати крок симплекс – методу.

1) Вибираємо найбільшу додатну оцінку δ₂ = 3. Зафарбуємо її у червоний колір. Тим самим обрані змінна х₂ і стовпець з номером 2 симплекс – таблиці.

2) , 3) Елементи у стовпці 2 додатні, отже треба застосувати умову допустимості. У чарунок F2 електронної симплекс – таблиці введемо формулу = E2/B2, а далі скопіюємо (протягнемо) її у чарунки F3 і F4. В результаті дістанемо:

	A	B	C	D	E	F
1	x1	x2	x3	x4	b	b/aij
2	2	6	1	0	10	1,666667
3	3	2	0	1	8	4
4	1	3	0	0	0

Мінімальне з отриманих значень Θ = 1,666667 у чарунці F2. Зафарбуємо його і ведучий елемент жорданова перетворення на перетині обраних рядка і стовпця у чарунці В2.

4) Жорданово перетворення: виокремимо нову симплекс – таблицю в діапазоні А6: F8. Надамо чарункам електронної таблиці таких значень:

	А	B	C	D	E	F
6	←	=В2/$В$2	→	→	→
7	←	=В3 – В6*$B$3	→	→	→
8	←	=В4 – В6*$B$4	→	→	→

В результаті дістанемо:

	A	B	C	D	E	F
6	0,333333	1	0,166667	0	1,666667
7	2,333333	0	-0,33333	1	4,666667
8	0	0	-0,5	0	-5

5) Маємо симплекс – таблицю з новим набором основних змінних х₂, х₄ , новий опорний розв’язок (0; 1,7; 0; 4,7), нове значення цільової функції f = 5.

6) Всі оцінки не додатні. Згідно з теоремою 1 це означає, що розв’язок і значення цільової функції є оптимальними. На цьому симплекс – метод завершує роботу. Відкидаючи додаткові змінні, дістаємо х₁ = 0 , х₂ ≈ 1,7. Тут те ж саме значення цільової функції, що й отримане за допомогою надбудови Поиск решения , проте ще один новий розв’язок, тут безумовно опорний.

Зазначимо, що оцінка δ₁ = 0, отже цільова функція, виражена через вільні змінні х₁, х₃ має вигляд f = 5 – 0,5х₃. Тому, якщо обрати за нову основну змінну х₁, то хоча її значення і стане додатним замість нульового, але значення цільової функції f не зміниться і ми дістанемо новий оптимальний опорний розв’язок. Отже, виконаємо ще одне жорданове перетворення. Елементи у стовпці 1 додатні, отже треба застосувати умову допустимості. В результаті дістанемо:

	A	B	C	D	E	F
	x1	x2	x3	x4	b	b/aij
6	0,333333	1	0,166667	0	1,666667	5
7	2,333333	0	-0,33333	1	4,666667	2
8	0	0	-0,5	0	-5
10	0	1	0,214286	-0,14286	1
11	1	0	-0,14286	0,428571	2
12	0	0	-0,5	0	-5

Новий опорний розв’язок (1;2; 0; 0), f = 5. Відкидаючи додаткові змінні, дістаємо х₁ = 1, х₂ = 2. Отже, існують принаймні два різних оптимальних опорних розв’язка. Зазвичай зрозуміти, проаналізувати ситуацію найкраще геометрично. На рисунку 4 множина Ω допустимих розв’язків – це чотирикутник OABCD, обмежений осями координат і прямими L₁: 2х₁ + 6х₂ = 10 і L₂: 3х₁ + 2х₂ = 8. Лінія нульового рівня цільової функції L₀: f = х₁ + 3х₂ = 0 перетинає початок координат О(0;0) і перпендикулярна вектору нормалі N(1;3). Цей вектор перпендикулярний також і прямій L₁, бо вектор нормалі N₁(2;6) прямої L₁ є колінеарним вектору N(1;3): 2 ∙ N = N₁. Тому, як і на рисунку 2, існує нескінченна множина оптимальних розв’язків даної задачі – всі точки відрізка АВ. Вершини відрізка А(0;1,7) і В(2;1) – це якраз ті опорні розв’язки, які і були отримані симплекс – методом. Як виявляється, у такій задачі надбудова Поиск решения знаходить просто деякі точки на АВ залежно від початкових даних.

х₂

4

3 N(1;3)

1,7 A

L₁

B

Ω L₂

O 1 C х₁

2,7 5

L₀

Рисунок 4.

Розглянемо ще один приклад математичної моделі.

f = 3х₁ + 2х₂ (max)

.

Складемо відповідну електронну таблицю:

	A	B	C	D
1	х1	х2	b
2	2	3	7	=СУММПРОИЗВ(A1:B1;$A$4:$B$4)
3	4	– 1	7	↓
4	3	2	f=	↓
5	1	1

Дістанемо

	A	B	C	D
1	х1	х2	b
2	2	3	7	5
3	4	-1	7	3
4	3	2	f=	5
5	1	1

Виділимо цільову чарунку D4 і оберемо Поиск решения у меню Сервис. Після слова Равной: обираємо варіант максимальному значению, у поле Изменяя ячейки вносимо адресу змінних А5:В5. У полі Ограничения: система обмежень цієї задачі: невід’ємність змінних у рядку 1, нерівність 2х₁ + 3х₂ ≥ 7 у рядку 2, 4х₁ – 2х₂ ≤ 7 у рядку 3.

Натиснемо на Выполнить. Дістанемо:

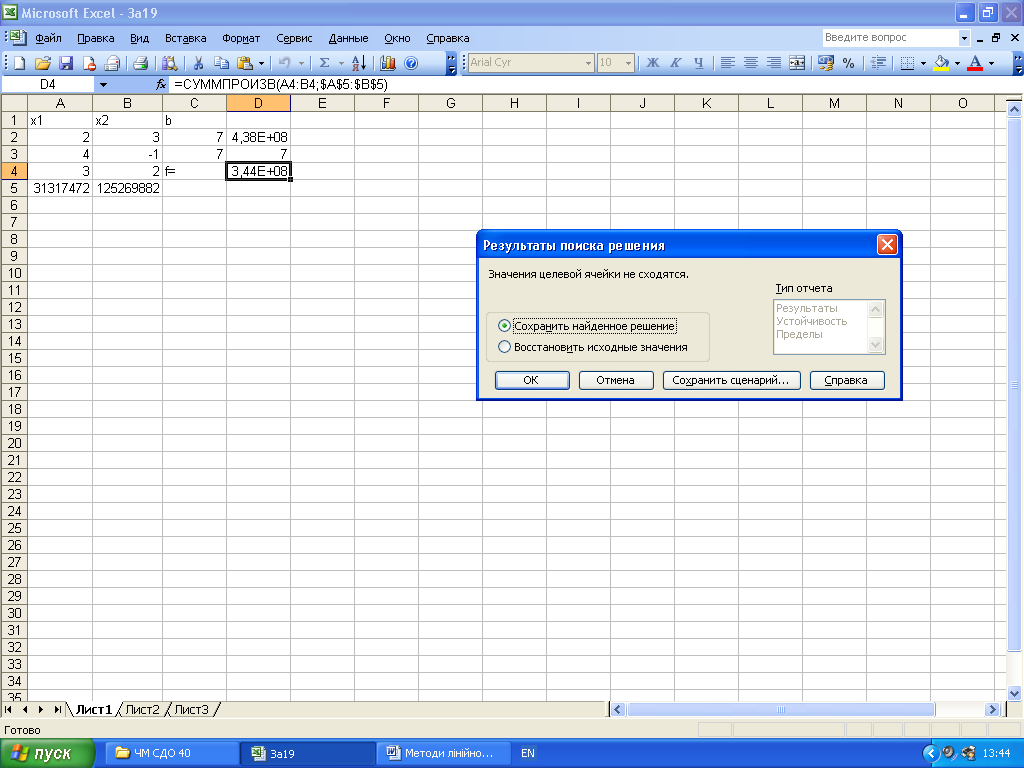
У вікні Результаты поиска решения повідомлення, що не відбулося збігу ітерацій, що і зрозуміло, бо надто великими є отримані результати: х₁ = 31317472, х₂ = 125269882, f = 3,44E+08 = 3,44∙10⁸. Навряд чи прибуток перевершив 10⁸, скоріше за все тут зовсім не існує розв’язка. Але чи так воно насправді? Розв’яжемо цю модель симплекс – методом.

1. Зведемо задачу до канонічної форми. Ввівши додаткові змінні х₃, х₄, отримуємо:

f = 3x₂ + 2x₁ (max)

.

Запишемо її у електронну симплекс – таблицю:

	A	B	C	D	E	F
1	x1	x2	x3	x4	b	b/aij
2	2	3	– 1	0	7
3	4	– 7	0	1	7
4	2	3	0	0	0

2. На відміну від попередніх прикладів тут нема початкового опорного розв’язку: нема діагональної матриці. Насправді ж він є необхідним, щоби започаткувати симплекс – метод. Належний вигляд уже має стовпець змінної x₄, до неї треба додати ще одну. Це не може бути x₃ бо для такого опорного розв’язку x₃ = – 7, тобто він не є допустимим. Це не може бути і x₁. Справді, застосуємо умову допустимості, яка є необхідною і достатньою для того, щоби отриманий в результаті жорданова перетворення опорний розв’язок виявився допустимим. Тут min {7/4, 7/2} досягається у рядку 3, тобто якщо у якості ведучого рядка обрати необхідний нам другий, то ми знову отримаємо недопустимий опорний розв’язок. Залишилась змінна x₂ , ведучий елемент жорданова перетворення у чарунці В2. Отже, виокремимо нову симплекс – таблицю в діапазоні А6: F8. Надамо чарункам електронної таблиці таких значень:

	А	B	C	D	E	F
6	←	=В2/$В$2	→	→	→
7	←	=В3 – В6*$B$3	→	→	→
8	←	=В4 – В6*$B$4	→	→	→

В результаті дістанемо:

	А	B	C	D	E	F
	x1	x2	x3	x4	b	b/aij
6	2/3	1	- 1/3	0	2 1/3
7	4 2/3	0	- 1/3	1	9 1/3
8	1 2/3	0	2/3	0	-4 2/3

Тут є додатна оцінка δ₃ = 2/3, а всі елементи стовпця С, окрім самої оцінки δ₃ недодатні.

Тому цільова функція не обмежена зверху (теорема 2, умова необмеженості цільової функції), тобто оптимального розв’язку даної задачі справді не існує. На рисунку 5 множина Ω допустимих розв’язків цієї задачі – це необмежений чотирикутник BACD, обмежений віссю координат Ох₂ і прямими L₁: 2х₁ + 3х₂ = 7 і L₂: 4х₁ – х₂ = 7. Лінія нульового рівня

х₂

B D

Ω L₂

A N(3;2)

L₀ C L₁

х₁

О

Рисунок 5

цільової функції L₀: f = 3х₁ + 2х₂ = 0 перетинає початок координат О(0;0) і

перпендикулярна вектору нормалі N(3;2). Як і на рисунку 3, при пересуванні у напрямку вектора N пряма, паралельна L₀ весь час буде перетинати область Ω, то цільова функція f не обмежена зверху на допустимих розв’язках. Тому не існує точки, у якій f набуває найбільшого можливого значення, тобто не існує оптимального розв’язка.