§6. Розв’язування задач лінійного програмування за допомогою excel

Спочатку розв’яжемо симплекс – методом за допомогою EXCEL економіко - математичну модель задачі планування виробництва, яка була першою сформульована у цьому розділі і вже розв’язана графічним методом у §2:

f = 200 х₁ + 300 х₂ (max)

.

Згідно з планом попереднього параграфу

1. Зведемо цю задачу лінійного програмування до канонічної форми. Ввівши додаткові змінні х₃, х₄, х₅, отримуємо

f = 200 х₁ + 300 х₂ (max)

Запишемо її у електронну симплекс – таблицю:

	A	B	C	D	E	F	G
1	x1	x2	x3	x4	x5	b	b/aij
2	10	20	1	0	0	100
3	20	10	0	1	0	100
4	15	15	0	0	1	90
5	200	300	0	0	0	0

Тут окрім стандартних стовпців симплекс – таблиці введений ще стовпець b/aij, у якому далі буде перевірятись умова допустимості.

2. Симплекс – таблиця виявляється приведеною до базису А₃ , А₄ , А₅ опорного розв’язку. Це видно з того, що матриця такого розв’язку на стовпцях змінних х₃ , х₄ , х₅ є діагональною, а оцінки основних змінних дорівнюють нулю. Отже, початковий опорний розв’язок α₁ = (0; 0; 0; 0; 18; 30; 40), f(α₁) = 0.

3. Серед оцінок базису є додатні, тож згідно з ознакою оптимальності α₁ не є оптимальним і отже треба виконати крок симплекс – методу.

1) Вибираємо найбільшу додатну оцінку δ₂ = 300. Зафарбуємо її в улюблений колір (тут червоний). Тим самим обрані змінна х₂ і стовпець з номером 2 симплекс – таблиці.

2) , 3) Елементи у стовпці 2 додатні, отже треба застосувати умову допустимості. У чарунок G2 електронної симплекс – таблиці введемо формулу = F2/B2, а далі скопіюємо (протягнемо) її у чарунки G3 і G4. В результаті дістанемо:

	A	B	C	D	E	F	G
1	x1	x2	x3	x4	x5	b	b/aij
2	10	20	1	0	0	100	5
3	20	10	0	1	0	100	10
4	15	15	0	0	1	90	6
5	200	300	0	0	0	0

Мінімальне з отриманих значень Θ = 5 у чарунці G2. Зафарбуємо її бажано в той самий колір. Тим самим обрані рядок 1 (для якого саме і виконується умова допустимості) і ведучий елемент жорданова перетворення на перетині обраних рядка і стовпця у чарунку В2. Зафарбуємо також і його.

4) Жорданово перетворення: треба рядок 2 поділити на 20, а від кожного рядка з решти відняти отриманий, помноживши його на відповідне число у стовпці В. Задамо відповідні формули у стовпці В електронної симплекс – таблиці, а в решту скопіюємо з нього. Отже,

виокремимо нову симплекс – таблицю в діапазоні А7: G10. Надамо чарункам електронної таблиці таких значень:

	А	B	C	D	E	F	G
7	←	=В2/$В$2	→	→	→	→
8	←	=В3 – В7*$B$3	→	→	→	→
9	←	=В4 – В7*$B$4	→	→	→	→
10	←	=В5 – В7*$B$5	→	→	→	→

Тут символ $ задає абсолютну адресацію: замість $В$2 можна задати прямо 20, замість $В$3 – 10. В результаті дістанемо:

	A	B	C	D	E	F	G
	x1	x2	x3	x4	x5	b	b/aij
7	0,5	1	0,05	0	0	5
8	15	0	-0,5	1	0	50
9	7,5	0	-0,75	0	1	15
10	50	0	-15	0	0	-1500

5) Маємо симплекс – таблицю з новим набором основних змінних х₂, х₄, х₅ (іншими словами з новим базисом), новий опорний розв’язок (0; 5; 0; 50; 15), нове значення цільової функції f = 1500.

6) На цьому перший крок симплекс – методу завершується. Треба розпочати другий крок з аналізу оцінок змінних і далі повторити всі попередні пункти.

Другий крок. 1) У симплекс – таблиці, отриманій на першому кроці, залишилась одна додатна оцінка у чарунці А10 δ₁ = 50, зафарбуємо її. Тим обрані змінна х₁ і стовпець з номером 1 симплекс – таблиці.

2), 3) Елементи в обраному стовпці додатні, отже треба застосувати умову допустимості. У чарунок G7 електронної симплекс – таблиці введемо формулу = F2/B2 і скопіюємо її у чарунки G8 і G9. В результаті дістанемо:

	A	B	C	D	E	F	G
	x1	x2	x3	x4	x5	b	b/aij
7	0,5	1	0,05	0	0	5	10
8	15	0	-0,5	1	0	50	3,333333
9	7,5	0	-0,75	0	1	15	2
10	50	0	-15	0	0	-1500

Зафарбуємо мінімальне з отриманих значень Θ = 2 у чарунці G9. Зафарбуємо також на перетині обраних рядка і стовпця ведучий елемент жорданова перетворення у чарунці А9.

4. Жорданово перетворення: виокремимо нову симплекс – таблицю в діапазоні А12: G15. Надамо чарункам електронної таблиці таких значень:

	А	B	C	D	E	F	G
12	=А7 – А14*$А$7	→	→	→	→	→
13	=А8 – А14*$А$8	→	→	→	→	→
14	=А9/$А$9	→	→	→	→	→
15	=А10 – А14*$А$10	→	→	→	→	→

Звичайно, що спочатку діємо у рядку 14, а потім у решті. В результаті дістанемо:

	A	B	C	D	E	F	G
	x1	x2	x3	x4	x5	b	b/aij
12	0	1	0,1	0	-0,06667	4
13	0	0	1	1	-2	20
14	1	0	-0,1	0	0,133333	2
15	0	0	-10	0	-6,66667	-1600

5) Маємо симплекс – таблицю з новим набором основних змінних х₁, х₂, х₄ (іншими словами з новим базисом), новий опорний розв’язок (2; 4; 0; 20; 0), нове значення цільової функції f = 1600.

6) Нарешті всі оцінки не додатні. Згідно з теоремою 1 це означає, що розв’язок (2; 4; 0; 20; 0) і значення цільової функції f = 1600 є оптимальними. На цьому симплекс – метод завершує роботу.

Загалом процес обчислень виглядає так:

	A	B	C	D	E	F	G
1	x1	x2	x3	x4	x5	b	b/aij
2	10	20	1	0	0	100	5
3	20	10	0	1	0	100	10
4	15	15	0	0	1	90	6
5	200	300	0	0	0	0
6
7	0,5	1	0,05	0	0	5	10
8	15	0	-0,5	1	0	50	3,333333
9	7,5	0	-0,75	0	1	15	2
10	50	0	-15	0	0	-1500
11
12	0	1	0,1	0	-0,06667	4
13	0	0	1	1	-2	20
14	1	0	-0,1	0	0,133333	2
15	0	0	-10	0	-6,66667	-1600

Відкинувши три останні додані змінні, дістаємо розв’язок початкової задачі х₁ = 2, х₂ = 4, той самий, що і графічним методом. Цей розв’язок можна отримати і використавши надбудову EXCEL “Пошук розв’язку”. Ця надбудова задачі лінійного програмування розв’язує симплекс – методом, проте відразу видає оптимальний розв’язок до заданої математичної моделі.

Спочатку запишемо дані задачі в електронну таблицю у форматі, схожому на формат симплекс – таблиці.

	A	B	C	D
1	x1	х2	b
2	10	20	100
3	20	10	100
4	15	15	90
5	200	300

Тут у рядки 2,3,4 занесена матриця обмежень цієї задачі лінійного програмування, у рядку 5 до неї додані коефіцієнти цільової функції. Тепер додамо до цього у рядку 6 поточні значення змінних х₁, х₂ (зазвичай найбільш зручно х₁ = 1, х₂ = 1); у стовпці D відповідні значення лівих частин системи обмежень при поточних значеннях змінних. Тут у чарунці D2 задана формула =СУММПРОИЗВ(А2:В2;$А$6:$В$6), яка обчислює скалярний добуток масиву А2:В2 на масив А6:В6, тобто значення 10х₁ + 20х₂ при поточних значеннях змінних х₁ = 1, х₂ = 1. У чарунки D3:D5 цю формулу копіюємо. В результаті дістанемо:

	A	B	C	D
1	х1	х2	b
2	10	20	100	30
3	20	10	100	30
4	15	15	90	30
5	200	300	f=	500
6	1	1

У чарунці D5 тут значення цільової функції при поточних значеннях змінних, виділимо її і далі в термінології надбудови “Пошук розв’язку” будемо називати цільовою. Тепер час обрати Поиск решения у меню Сервис. (Якщо його нема в меню Сервис, то оберіть там команду Надстройки і у вікні діалогу Список надстроек встановіть прапорець Поиск решения). Адреса D5 з’явиться у полі Целевая ячейка вікна Поиск решения.

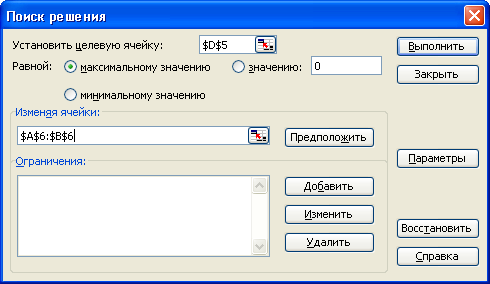
Після слова Равной: оберемо варіант максимальному значению. У поле Изменяя ячейки треба внести адресу змінних – діапазон А6:В6; виділимо його, коли курсор знаходиться у цьому полі, і ця адреса там з’явиться автоматично. У поле Ограничения треба внести систему обмежень. Натиснімо на кнопку Добавить, з’явиться наступне вікно діалогу:

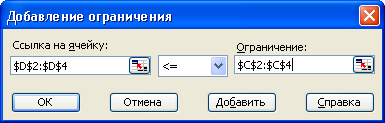
Воно складається з трьох частин. У поле Ссылка на ячейку треба внести адресу чарунок, які містять значення лівих частин системи обмежень при поточних значеннях змінних, що підлягають обмеженню. Коли курсор знаходиться у цьому полі, виділимо чарунки D2:D4 і вони з’являться там. У центрі умова обмеження, яку треба вибрати із списку: в даному випадку це ≤ . У поле Ограничение: треба внести його значення безпосередньо або адресу чарунки, де воно знаходиться. Коли курсор у цьому полі, виділимо чарунки С2:С4 і вони з’являться там. Тим самим задані три обмеження: 10х₁ + 20х₂ ≤ 100, 20х₁ + 10х₂ ≤ 100, 15х₁ + 15х₂ ≤ 90 одночасно. Натиснімо на Добавить, щоби прийняти ці обмеження і перейти до наступних. У системі обмежень ще залишилась умова х_j ≥ 0 (j = 1,2). Так само внесемо у поле Ссылка на ячейку чарунки А6:В6, у центрі виберемо ≥ із списку, у полі Ограничение безпосередньо з клавіатури задамо 0.

Натиснімо на ОК, щоби прийняти ці обмеження і повернутись до вікна Поиск решения.

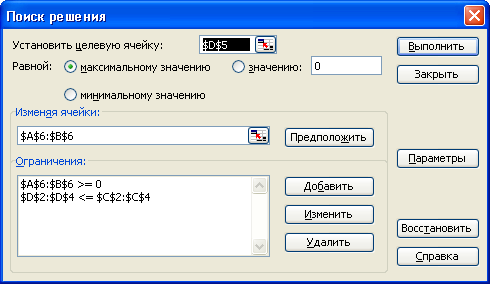
Тепер у цьому вікні вся економіко – математична модель даної задачі лінійного програмування: адреса цільової функції, вибір максимуму або мінімуму, адреса змінних, система обмежень. Натиснемо на Выполнить.

Відповідь можна знайти безпосередньо у чарунках змінних А6:В6 х₁ = 2, х₂ = 4, той самий, що і раніше. Вікно Результаты поиска решения повідомляє, що розв’язок знайдений при заданих обмеженнях. Якщо обрати Восстановить исходное значение, у полі Тип отчёта обрати Результаты і натиснути ОК, то у таблиці даних відтворяться початкові значення чарунок, а на окремому листі буде створений наступний звіт, який ми побачимо, якщо натиснути на Отчёт по результатам 1

Microsoft Excel 11.0 Отчет по результатам
Рабочий лист: [Поиск.xls]Лист1
Отчет создан: 06.02.2010 13:00:35
Целевая ячейка (Максимум)
	Ячейка	Имя	Исходное значение	Результат
	$D$5	f=	500	1600
Изменяемые ячейки
	Ячейка	Имя	Исходное значение	Результат
	$A$6	x1	1	2
	$B$6	x2	1	4

По суті це відповідь даної задачі, створена у EXCEL. Розглянемо ще один приклад застосування надбудови Поиск решения – транспортну задачу, що була сформульована у §1. Це досить специфічний приклад задачі лінійного програмування, для розв’язання якої зазвичай використовують не симплекс – таблицю, а дещо іншу таблицю, яку і називають транспортною. Перш за все запишемо таку таблицю для даної задачі на лист EXCEL:

	A	B	C	D	E
1		М1	М2	М3
2	Р1	1	3	4	12
3	Р2	2	5	3	8
4	Р3	6	7	4	10
5		6	9	15	30

Фактично це таблиця вартості перевезень, наведена в умові задачі, до якої додані рядок попиту пунктів призначення знизу і праворуч стовпець ваги вантажу, що треба вивезти з пунктів відправлення. Для змінних – ваги вантажу, запланованого для перевезення з пункту Р_i до пункту М_j (i, j = 1,2,3) – відведемо ще одну таблицю в діапазоні В8:D10, схожу на попередню. Як і раніше, зазвичай найбільш зручно у ці чарунки задати одиниці.

	A	B	C	D	E
1		М1	М2	М3
2	Р1	1	3	4	12
3	Р2	2	5	3	8
4	Р3	6	7	4	10
5		6	9	15	30
6	Вартість	9	15	11	35
7
8		1	1	1	3
9		1	1	1	3
10		1	1	1	3
11		3	3	3

У чарунку В11 задамо формулу = СУММ(B8:B10) – це сумарна вага вантажу до пункту призначення М1: тут 3, оскільки всі змінні дорівнюють 1. (Можна виділити В11 і натиснути на ∑ (Автосумма) на стандартній панелі EXCEL і формула з’явиться там автоматично). Скопіюємо цю формулу у чарунки В12 і В13 для пунктів призначення М2 і М3. Аналогічно у чарунці Е8 формула =СУММ(B8:D8) – це сумарна вага вантажу з пункту відправлення Р1; скопіюємо цю формулу у чарунки Е9 і Е10 для Р2 і Р3. Рядок 6 під транспортною таблицею призначений для цільової функції, вартості в цій задачі (як це і у симплекс – таблиці). У чарунку В6 задамо формулу =СУММПРОИЗВ(B2:B4;B8:B10) – це вартість перевезень до М1 за даним планом перевезень, скопіюємо її у С6 і D6 для М2 і М3. У чарунку Е6 запишемо формулу = СУММ(B6:D6) – це значення цільової функції при поточних значеннях змінних, а Е6 в термінології надбудови “Пошук розв’язку” є цільовою чарункою. Виділимо її і тепер час обрати Поиск решения у меню Сервис.

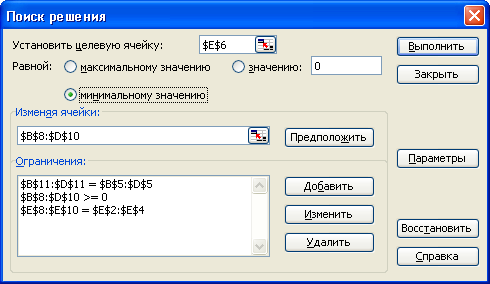
У цьому вікні вся економіко – математична модель даної задачі лінійного програмування. А саме після слова Равной: обираємо варіант минимальному значению, тобто забезпечуємо вимогу, щоби загальна вартість перевезень була мінімальною. У поле Изменяя ячейки вносимо адресу змінних – діапазон В8:D10. У полі Ограничения (як і раніше, через вікно діалогу Добавление ограничений) виписана система обмежень цієї задачі, отримана у формульному вигляді в §1. Тут у першому рядку забезпечується вимога, щоби повністю був задоволений попит пунктів призначення; у третьому, щоби весь вантаж був вивезений з пунктів відправлення; у другому вимога невід’ємності змінних, тобто ваги вантажу. Натиснемо на Выполнить.

Вікно Результаты поиска решения повідомляє, що розв’язок знайдений при заданих обмеженнях. Оберемо Восстановить исходное значение і Результаты у полі Тип отчёта. Якщо тепер натиснути ОК, то у таблиці даних відтворяться початкові значення чарунок, а на окремому листі буде сформована відповідь, яку ми побачимо, якщо натиснути на

Отчёт по результатам 1.

Microsoft Excel 11.0 Отчет по результатам
Рабочий лист: [Поиск.xls]Лист2
Отчет создан: 06.02.2010 21:39:45
Целевая ячейка (Минимум)
	Ячейка	Имя	Исходное значение	Результат
	$E$6	Вартість	35	91,00000267
Изменяемые ячейки
	Ячейка	Имя	Исходное значение	Результат
	$B$8	М1	1	3,000000667
	$C$8	М2	1	9
	$D$8	М3	1	0
	$B$9	М1	1	2,999999333
	$C$9	М2	1	0
	$D$9	М3	1	5,000000667
	$B$10	М1	1	0
	$C$10	М2	1	0
	$D$10	М3	1	10,00000033

Отже, х₁₁ = 3, х₂₁ = 3, х₃₁ = 0, х₁₂ = 9, х₂₂ = 0, х₃₂ = 0, х₁₃ = 0, х₂₃ = 5, х₃₃ = 10. У термінах початкової задачі це означає, що вага вантажу з Р1 до М1 3 т, з Р2 до М1 3 т, з Р3 до М1 0, з Р1 до М2 9 т, … ; мінімальне можливе значення вартості дорівнює 91 грошовій одиниці.