3. Множення матриць.

Добуток m n – матриці А на n p матрицю В – це така m р – матриця С = АВ, елемент с_ij якої є скалярним добутком вектор – рядка і матриці А на вектор – стовпець j матриці В. Добуток 2  3 матриці А = на 2  2 матрицю В = С = АВ не існує, оскільки число стовпців матриці А дорівнює 3 і не дорівнює числу рядків матриці В.

Для множення матриць є спеціальний вбудований оператор Excel МУМНОЖ. Наприклад, у наступній електронній таблиці

	A	B	C	D	E	F
1	3	-5		5	0	-4
2	4	0		3	1	7
3	-7	2

задані 3  2 матриця А = і 2  3 матриця В = . Для знаходження 3  3 матриці С = АВ виділимо діапазон А5:С7 і (можливо за допомогою вікна цього оператора) введемо в нього формулу =МУМНОЖ(А1:В3;D1:F2).

	A	B	C	D	E	F
1	3	-5		5	0	-4
2	4	0		3	1	7
3	-7	2
4
5	=МУМНОЖ(А1:В3;D1:F2)
6
7

Після цього, притримуючи кнопки Alt i Shift, треба натиснути не Enter. В результаті отримаємо матрицю С:

	A	B	C	D	E	F
1	3	-5		5	0	-4
2	4	0		3	1	7
3	-7	2
4
5	0	-5	-47
6	20	0	-16
7	-29	2	42

Якщо спробувати помножити матриці А і В з нерівними числами стовпців у А та рядків у В, то отримаємо повідомлення про помилку #ЗНАЧ! .

4. Матриця, обернена до квадратної матриці А порядку n – це така квадратна матриця А^-1 того ж порядку, що А А^-1 = А^-1 А = Е, де Е – одинична матриця. Якщо А має обернену, то її можна знайти методом Гаусса.

Розглянемо n  2n матрицю АЕ, яку можна отримати, дописавши праворуч від матриці А одиничну матрицю того ж порядку. Наприклад, якщо А = 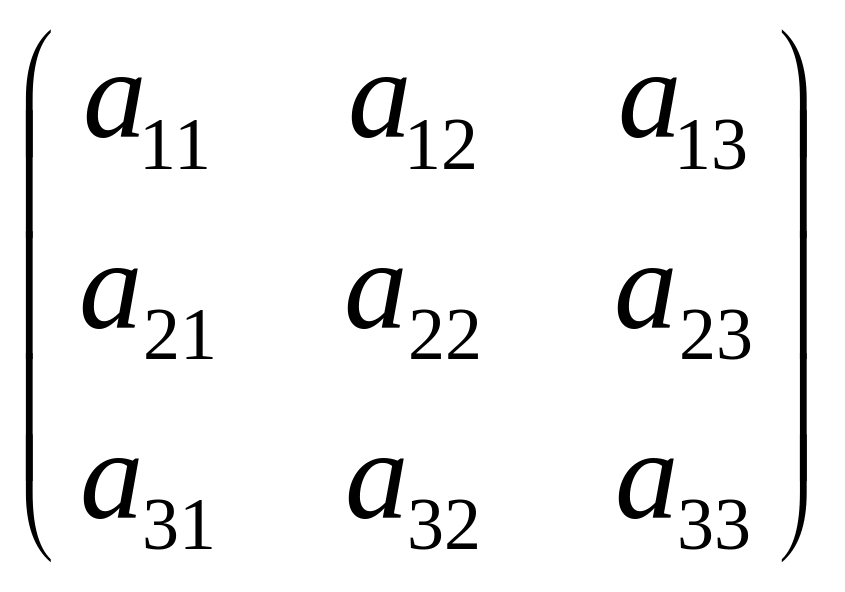, то АЕ = 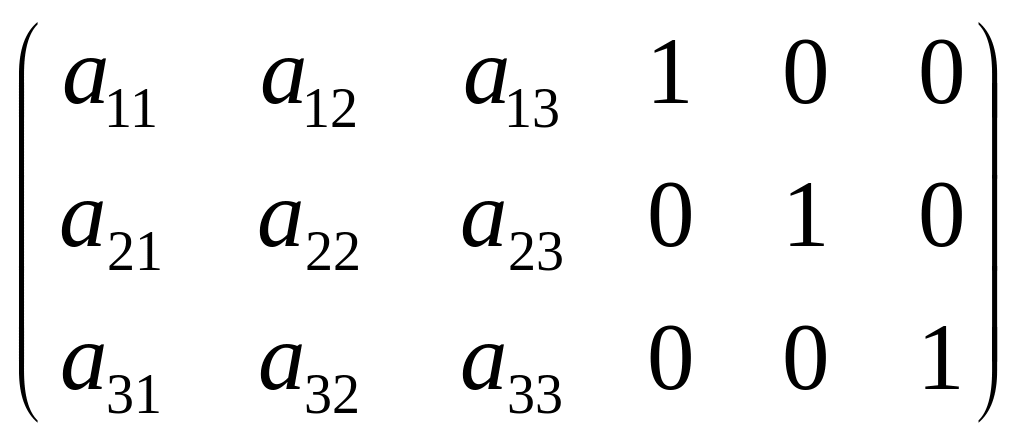. Зведемо матрицю АЕ до діагональної форми методом Гаусса. Тоді вона отримає вигляд ЕВ, де В – деяка квадратна матриця порядку n. Наприклад при n = 3 ЕВ = 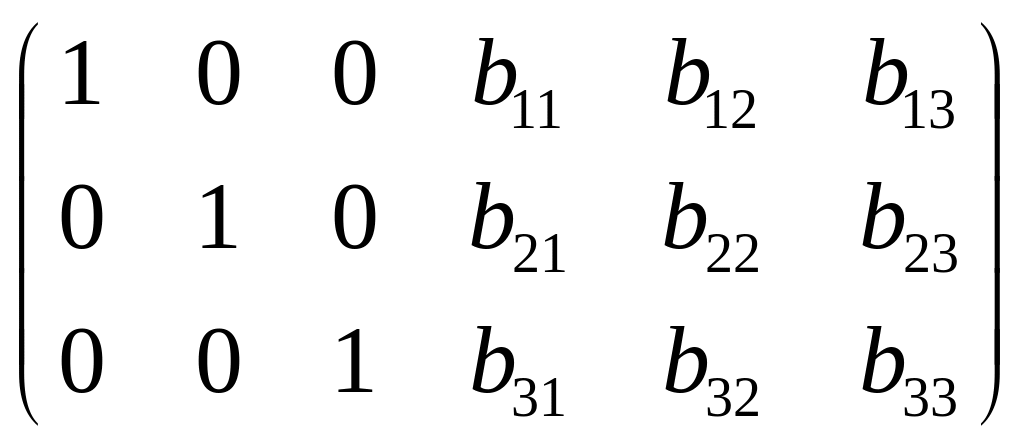. Стверджується, що така матриця В і є обернена до А, тобто В = А^-1.

Справді, як ми бачили вище, якщо звести до діагональної форми СЛР з матрицею системи А, то стовпець вільних членів у розширеній матриці цієї системи є розв’язком даної СЛР. Тому перший стовпець матриці В є розв’язком СЛР Ах = , наприклад, = , тобто 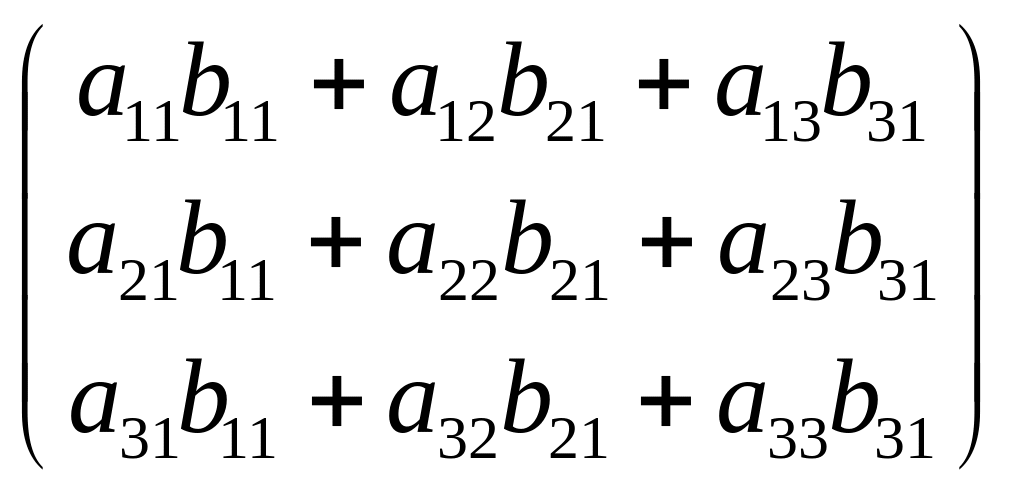= . Аналогічно другий стовпець матриці В є розв’язком СЛР Ах = , наприклад, = , тобто = , … . Але за означенням множення матриць це означає, що АВ = Е, тобто В = А^-1.

Задача 2. Знайти матрицю, обернену до матриці А = 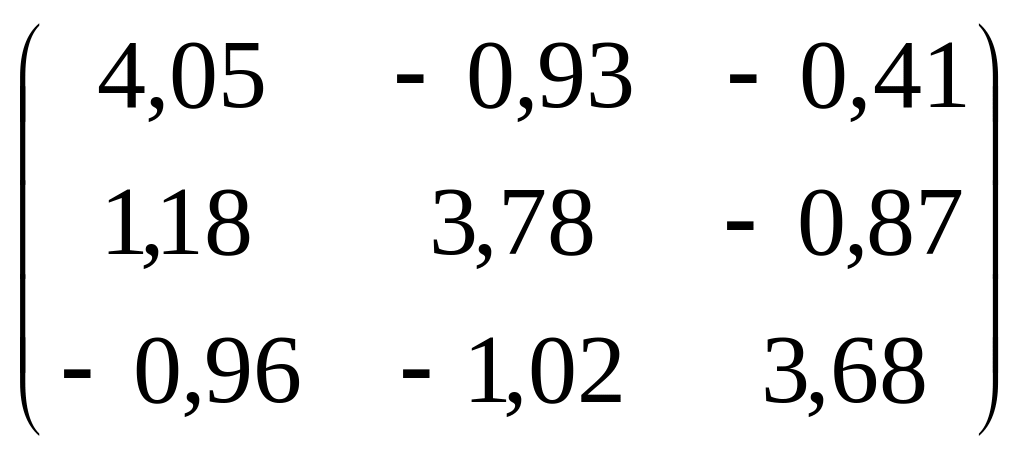методом Гаусса.

Розв’язання. Задамо в електронній таблиці матрицю АЕ:

	A	B	C	D	E	F
1	4,05	-0,93	-0,41	1	0	0
2	1,18	3,78	-0,87	0	1	0
3	-0,96	-1,02	3,68	0	0	1

Зведемо її до діагональної так само, як і в попередньому параграфі:

	A	B	C	D	E	F
1	4,05	-0,93	-0,41	1	0	0
2	1,18	3,78	-0,87	0	1	0
3	-0,96	-1,02	3,68	0	0	1
4
5	1	-0,22963	-0,10123	0,246914	0	0
6	0	4,050963	-0,75054	-0,29136	1	0
7	0	-1,24044	3,582815	0,237037	0	1
8
9	1	0	-0,14378	0,230398	0,056685	0
10	0	1	-0,18528	-0,07192	0,246855	0
11	0	0	3,352991	0,14782	0,30621	1
12
13	1	0	0	0,236737	0,069816	0,042881
14	0	1	0	-0,06376	0,263775	0,055257
15	0	0	1	0,044086	0,091324	0,298241

0,236737 0,069816 0,042881

Отже, матриця В = –0,06376 0,263775 0,055257 є оберненою до матриці А. Це

0,044086 0,091324 0,298241

можна перевірити безпосередньо за означенням за допомогою вбудованого оператора МУМНОЖ. Результат множення А на В, тобто результат дії оператору МУМНОЖ(A1:C3; D13:F15) дорівнює

1	-3,46945E-17	-1,38778E-17
6,25E-17	1	-5,55112E-17
0	-5,55112E-17	1

Оскільки числа ~ 10^-17 з точки зору Excel не відрізняються від нуля, то отримана матриця є одиничною. Якщо є сумнів, то можна змінити формат чарунки з общий на числовой . Тоді дістанемо

1,00	0,00	0,00
0,00	1,00	0,00
0,00	0,00	1,00

Знайти обернену матрицю можна також і за допомогою спеціального вбудованого оператора Excel МОБР. Треба виділити квадратний діапазон того ж розміру, що й у даної матриці, (в цьому прикладі з 9 чарунок), задати в ньому цей оператор, єдиним аргументом якого є діапазон даної матриці (тут це МОБР(А1:С3) ) і притримуючи кнопки Alt i Shift, натиснути не Enter. Результат в даному випадку просто співпадає з отриманим вище методом Гаусса.

Звичайно, не кожна квадратна матриця А має звернену, тільки та, визначник якої не дорівнює нулю: А  0. Тому перед безпосереднім розв’язуванням задачі 2 було б доцільно знайти визначник даної матриці. Це можна зробити за допомогою відповідного вбудованого оператора Excel МОПРЕД. Треба виділити чарунку і задати там цей оператор, єдиним аргументом якого є діапазон заданої матриці. Після цього можна натиснути ОК або Enter: на відміну від МОБР та МУМНОЖ результатом дії цього оператора є числове значення, а не масив чарунок. В даному прикладі формула МОПРЕД(А1:С3) дає значення визначника А = 55,01051.

Якщо значення визначника матриці відмінне від нуля, але досить мале порівняно з її елементами, то відповідна СЛР погано обумовлена. СЛР називають добре обумовленою, якщо малі збурення коефіцієнтів мало збурюють її розв’язки і в противному разі погано обумовленою. Наприклад, СЛР , розв’язком якої є пара (1; 0) погано обумовлена. Справді, якщо число 6,1 у правій частині першого рівняння змінити на 0,02, то СЛР матиме розв’язком пару (5,1; - 7,35). Якщо коефіцієнт 6,1 у лівій частині першого рівняння змінити на 0,01, то розв’язком СЛР буде пара (0,36730972; 1,204918). Причиною поганої обумовленості цієї системи є її майже виродженість: її визначник дорівнює 0,04 і становить лише 0,27% значення найбільшого з коефіцієнтів системи 14,7.