Питання, тести
Відрізок [a;b] є відрізком ізоляції кореня рівняння , якщо
А |
графік
похідної
|
Б |
графік похідної не перетинає вісь абсцис на (a;b) |
В |
графік
функції
|
Г |
умови Б та В виконані одночасно |
Д |
графік функції не перетинає вісь абсцис на (a;b) |
Е |
умови А та Д виконані одночасно |
Ж |
це залежить від функції |
перетинає вісь абсцис на (a;b)
перетинає вісь абсцис на (a;b)
Нехай графік функції перетинає вісь абсцис по інтервалу (0;1). Тоді відрізок [0;1] є відрізком ізоляції кореня рівняння , якщо
А |
> 2x + 1 |
Б |
< 2x + 1 |
В |
< 2x – 2 |
Г |
> 2x – 2 |
3. Нехай графік функції перетинає вісь абсцис по інтервалу (0;1). Тоді відрізок [0;1] є відрізком ізоляції кореня рівняння , якщо графік похідної такий:
А:
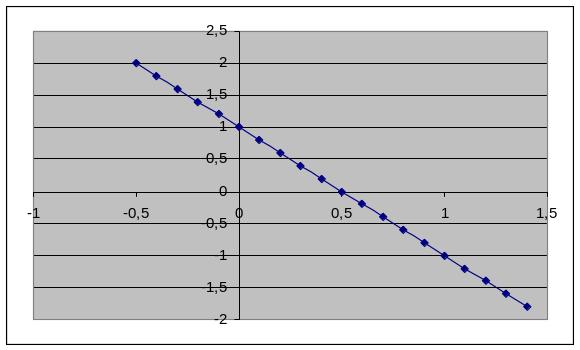
Б:
В:
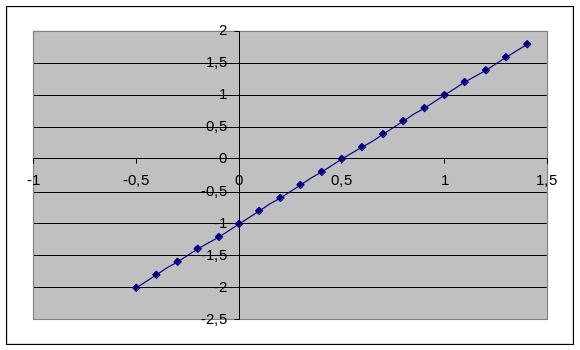
Г:
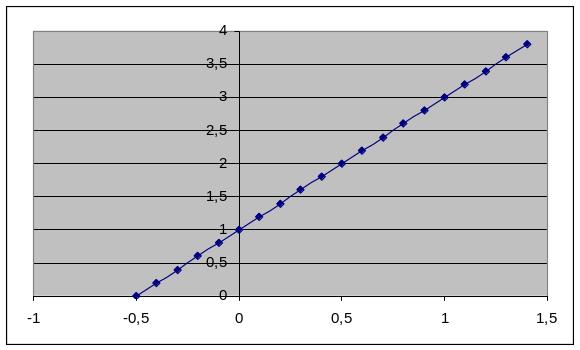
Нехай на інтервалі (a;b) графік функції перетинає вісь абсцис, < 0. Тоді метод дихотомії на відрізку [a;b] визначають такі формули: сn = (аn + bn)/2 та
А |
|
Б |
|
В |
|
Г |
|
5. Нехай на інтервалі (0;1) графік функції перетинає вісь абсцис, < 0. Тоді метод дихотомії на відрізку [a;b] визначають такі формули:
А:
|
A |
B |
C |
D |
1 |
0 |
1 |
= (A1 + B1)/2 |
= 2^C1 – 4*C1 + 1 |
2 |
= ЕСЛИ(D1 > 0; C1; B1) |
= ЕСЛИ(D1 > 0; A1;C1) |
↓ |
↓ |
3 |
↓ |
↓ |
↓ |
↓ |
Б:
|
A |
B |
C |
D |
1 |
0 |
1 |
= (A1 + B1)/2 |
= 2^C1 + 5*C1 – 3 |
2 |
= ЕСЛИ(D1 > 0; A1; C1) |
= ЕСЛИ(D1 > 0; C1; B1) |
↓ |
↓ |
3 |
↓ |
↓ |
↓ |
↓ |
В:
|
A |
B |
C |
D |
1 |
0 |
1 |
= (A1 + B1)/2 |
= 2^C1 – 4*C1 + 1 |
2 |
= ЕСЛИ(D1 > 0; C1; B1) |
= ЕСЛИ(D1 > 0; A1;C1) |
↓ |
↓ |
3 |
↓ |
↓ |
↓ |
↓ |
Г:
|
A |
B |
C |
D |
1 |
0 |
1 |
= (A1 + B1)/2 |
= 2^C1 + 5*C1 – 3 |
2 |
= ЕСЛИ(D1 > 0; A1; C1) |
= ЕСЛИ(D1 < 0; C1; B1) |
↓ |
↓ |
3 |
↓ |
↓ |
↓ |
↓ |
6. В наступній таблиці у стовпці А значення аргументу, у стовпці В відповідні значення функції . Чи можна стверджувати, що цими даними визначений корінь рівняння = 0 з точністю 10-6 ?
|
A |
B |
1 |
0,34581 |
-8,6E-05 |
2 |
0,345818 |
-4,1E-05 |
3 |
0,345821 |
-1,9E-05 |
4 |
0,345823 |
-7,5E-06 |
5 |
0,345824 |
-1,9E-06 |
А |
Б |
В |
Г |
так |
ні |
це залежить від функції |
це залежить від методу обчислень |
7. В наступній таблиці у стовпці А значення аргументу, у стовпці В відповідні значення функції . Чи можна стверджувати, що цими даними визначений корінь рівняння = 0 з точністю 10-5 ?
|
A |
B |
1 |
0,345825 |
1,65E-07 |
2 |
0,345825 |
-1,9E-07 |
3 |
0,345825 |
-1E-08 |
4 |
0,34583 |
2,94E-05 |
5 |
0,34582 |
-2,9E-05 |
А |
Б |
В |
Г |
так |
ні |
це залежить від функції |
це залежить від методу обчислень |
8. За таким варіантом наступного рисунку ітераційний процес х = φ(х) з початковою точкою А0 (х0, φ(х0)) збігається:
в г
А |
Б |
В |
Г |
а |
б |
в |
г |
Нехай │φ′(х)│< 1 на відрізку [a; b], φ(х*) = х* для деякого х* [a; b]. Тоді
А |
y = φ(х) є стискуючим відображенням на [a;b] |
Б |
[a; b] – відрізок ізоляції кореня х* |
В |
ітераційний процес хk = φ(хk-1) збігається до х* з довільним початковим х0 [a; b] |
Г |
збіжність характеризується нерівністю │ хk – x*│≤ qk│х0 – x*│, де q < 1 – довільне |
Для ефективних ітераційних методів (тобто з малою константою Ліпшиця q) після деякої кількості кроків
А |
похибками метода та неусувною можна нехтувати порівняно з похибкою обчислень |
Б |
ітерації не збігаються до кореня, а коливаються біля нього в околі похибки обчислень |
В |
критерій закінчення: значення двох послідовних ітерацій співпадають з даним числом значущих цифр |
Г |
критерій закінчення: значення достатньої кількості послідовних ітерацій співпадають один з одним з даним числом значущих цифр |
Найкраще (тобто найменше) можливе значення константи Ліпшиця функції φ(х) = х – λ f(x) на відрізку [a;b] ізоляції кореня рівняння f(x) = 0 дорівнює q = 1 – m1/М1, де М1 = , m1 = . При цьому
А |
Б |
В |
Г |
λ = 1/М1, λ > 0 |
λ = 1/М1, < 0 |
λ = 1/М1, > 0 |
│λ│= 1/М1, > 0 |
13. Нехай рівняння f(x) = 0 має корінь на відрізку його ізоляції [-1;-0,6], │f ′(-1)│≈ 3,08 │f ′(-0,6)│≈ 2,85; графік похідної f ′(x) наведений далі.
Тоді збіг ітераційного процесу хn+1 = φ(хn), де φ(х) = х – λ f(x) до кореня рівняння f(x) = 0 буде найшвидшим, якщо λ =
А |
Б |
В |
Г |
1/3,08 |
1/2,85 |
– 1/3,08 |
– 1/2,85 |
Рівняння f(x) = 2sin x – x2 + 2 = 0 має корінь на відрізку його ізоляції [1,8; 2,2], │f′(1,8)│≈ 4,05; │f′(2,2)│≈ 5,57; графік похідної f ′(x) наведений далі.
Тоді наступна таблиця визначає ітераційний процес хn+1 = φ(хn), де φ(х) = х – λ f(x), збіг якого до кореня рівняння f(x) = 0 буде найшвидшим:
А:
|
A |
B |
С |
1 |
1,8 |
= 2 ∙ sin(А1) – А1^2 + 2 |
= 1/ 4,05 |
2 |
= A1 – C1*B1 |
↓ |
|
3 |
↓ |
↓ |
|
Б:
|
A |
B |
С |
1 |
1,8 |
= 2 ∙ sin(А1) – А1^2 + 2 |
= 1/5,57 |
2 |
= A1 – $C$1*B1 |
↓ |
|
3 |
↓ |
↓ |
|
В:
|
A |
B |
С |
1 |
1,8 |
= 2 ∙ sin(А1) – А1^2 + 2 |
= – 1/ 4,05 |
2 |
= A1 – $C$1*B1 |
↓ |
|
3 |
↓ |
↓ |
|
Г:
|
A |
B |
С |
1 |
1,8 |
= 2 ∙ sin(А1) – А1^2 + 2 |
= – 1/5,57 |
2 |
= A1 – $C$1*B1 |
↓ |
|
3 |
↓ |
↓ |
|
15. Нехай хn+1 = φ(хn) – ітераційний процес, де φ(х) = х – λ f(x). Тоді за методом Ньютона λ =
А |
Б |
В |
Г |
1/М1 |
1/m1 |
|
|
16. [0; 1] є відрізком ізоляції кореня рівняння f(x) = 2х + 5x – 3 = 0. На цьому відрізку
А |
умови методу Ньютона не виконуються |
Б |
умови методу Ньютона виконуються і за початкову точку можна взяти 0 |
В |
умови методу Ньютона виконуються і за початкову точку можна взяти 1 |
Г |
умови методу Ньютона виконуються і за початкову точку можна взяти будь – яку точку відрізку [0;1] |
17. [0;1] є відрізком ізоляції кореня рівняння f(x) = 2х + 5x – 3 = 0. Наступна таблиця визначає ітераційний процес пошуку кореня рівняння f(x) = 0 методом Ньютона:
А:
|
A |
B |
C |
1 |
1 |
= 2^A1 + 5*A1 – 3 |
= 2^A1*ln2 + 5 |
2 |
= A1 – B1/$C$1 |
↓ |
|
3 |
↓ |
↓ |
|
Б:
|
A |
B |
C |
1 |
0 |
= 2^A1 + 5*A1 – 3 |
= 2^A1*ln2 + 5 |
2 |
= A1 – B1/$C$1 |
↓ |
|
3 |
↓ |
↓ |
|
В:
|
A |
B |
C |
1 |
1 |
= 2^A1 + 5*A1 – 3 |
= 2^A1*ln2 + 5 |
2 |
= A1 – B1/C1 |
↓ |
↓ |
3 |
↓ |
↓ |
↓ |
Г:
|
A |
B |
C |
1 |
0 |
= 2^A1 + 5*A1 – 3 |
= 2^A1*ln2 + 5 |
2 |
= A1 – B1/C1 |
↓ |
↓ |
3 |
↓ |
↓ |
↓ |
Збіг ітераційного процесу хk = φ(хk-1) тим швидший, чим порядок його збіжності
А |
Б |
В |
Г |
більший |
менший |
це залежить від φ(х) |
це залежить від початкової точки процесу |
Порядок збіжності ітераційного процесу α дорівнює
А |
0 для методу дихотомії |
Б |
1 для методу простої ітерації |
В |
2 для методу Ньютона |
Г |
2 для методу хорд |
20. [0; 1] є відрізком ізоляції кореня рівняння f(x) = 2х + 5x – 3 = 0. На цьому відрізку
А |
умови методу лінійного інтерполювання не виконуються |
Б |
умови методу хорд виконуються і за початкову точку можна взяти 0 |
В |
умови методу хорд виконуються і за початкову точку можна взяти 1 |
Г |
умови методу хорд виконуються і за нерухомий кінець можна взяти 1 |
21. [0;1] є відрізком ізоляції кореня рівняння f(x) = 2х + 5x – 3 = 0. Наступна таблиця визначає ітераційний процес пошуку кореня рівняння f(x) = 0 методом хорд:
А:
|
A |
B |
C |
D |
1 |
1 |
= 2^A1 + 5*A1 – 3 |
0 |
= 2^C1 + 5*C1 – 3 |
2 |
= A1 – B1*(A1 – C1)/(B1 – D1) |
↓ |
|
|
3 |
↓ |
↓ |
|
|
Б:
|
A |
B |
C |
D |
1 |
0 |
= 2^A1 + 5*A1 – 3 |
1 |
= 2^C1 + 5*C1 – 3 |
2 |
= A1 – B1*(A1 – C1)/(B1 – D1) |
↓ |
|
|
3 |
↓ |
↓ |
|
|
В:
|
A |
B |
C |
D |
1 |
1 |
= 2^A1 + 5*A1 – 3 |
0 |
= 2^C1 + 5*C1 – 3 |
2 |
= A1 – B1*(A1 – $C$1)/(B1 – $D$1) |
↓ |
|
|
3 |
↓ |
↓ |
|
|
Г:
|
A |
B |
C |
D |
1 |
0 |
= 2^A1 + 5*A1 – 3 |
1 |
= 2^C1 + 5*C1 – 3 |
2 |
= A1 – B1*(A1 – $C$1)/(B1 – $D$1) |
↓ |
|
|
3 |
↓ |
↓ |
|
|