§ 2. Метод дихотомії (поділу відрізка пополам)

Позначимо через точне значення кореня рівняння на відрізку ізоляції , а через ε – його задану абсолютну похибку. Суть методу в тому, що відрізок ділять пополам точкою і обчислюють . Якщо , то є точним значенням кореня. Якщо , а , то і значення буде шуканим наближенням коренем. Якщо і , то обирають той з двох відрізків і , на кінцях якого функція набуває значень протилежних знаків. Позначимо цей відрізок . Далі відрізок точкою знов ділять пополам і роблять так само, як і для відрізка В результаті процесу ділення відрізків пополам дістають послідовність вкладених відрізків , , , ..., , ..., кожен з яких містить точне значення кореня . Довжина відрізка дорівнює , тому = 0. Звідси випливає, що для деякого , а – наближене значення з заданою абсолютною похибкою оскільки

Розглянемо реалізацію методу дихотомії за допомогою електронних таблиць Excel на наступній задачі: розв‘язати рівняння f(x) = 2^х + 5x – 3 = 0 з точністю  = 0.5*10^-5.

1. Завжди корисно поглянути на графік функції і це дуже легко зробити за наявності Excel. Побудуємо електронну таблицю, а за її допомогою Майстром діаграм графік.

-5	27,9688
-4	22,9375
-3	-17,875
-2	-12,75
-1	-7,5
0	-2
1	4
2	11
3	20
4	33
5	54

У першому стовпці електронної таблиці – довільні точки із області визначення функції, у другому – значення функції f(x) = 2^х + 5x – 3 у цих точках. Відрізок [-5;5] та крок 1 тут обрані досить довільно, однак зазначимо, що на [-10;10] графік виглядає так, що їм важко

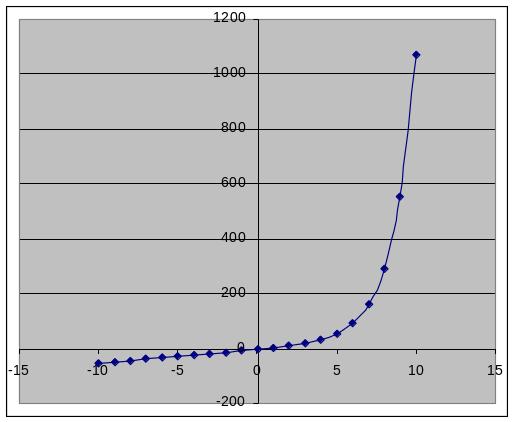
було б скористатись для локалізації коренів. На графіку з [-5;5] функція монотонно зростає і змінює знак лише на [0;1].

2. Тут можна застосувати аналітичний метод відокремлення коренів: f′(x) = 2^х ∙ ln2 + 5, f′(x) > 0 при всіх х, оскільки ln2 > 0. Отже рівняння f′(x) = 0 не має розв’язків, тобто критичних точок нема, вся вісь – область зростання функції f(x), існує не більш як один нуль f(x). З графіку бачимо, що функція змінює знак на [0;1]. На [0;1] виконуються умови теореми 1, отже це єдиний відрізок ізоляції кореня.

3. Нарешті знайдемо корінь на [0;1] з точністю  = 0.5*10^-5 методом дихотомії за допомогою Excel. У данному випадку а = 0, b = 1; нехай с = (а + b)/2. Оскільки f(x) зростає, то . Надамо чарункам електронної таблиці таких значень:

	A	B	C	D
1	0	1	= (A1 + B1)/2	= 2^C1 + 5*C1 – 3
2	= ЕСЛИ(D1 > 0; A1; C1)	= ЕСЛИ(D1 > 0; C1; B1)	↓	↓
3	↓	↓	↓	↓

Тут у чарунки А1 та В1 занесені початкові точки відповідно а = 0, b = 1, у С1 (а + b)/2, у D1 значення функції f(x) при х = С1, у А2 та В2 знаходяться значення відповідно а₁ та b₁, обрахованих у залежності від значення функції f(x) у D1. Символ ↓ означає копіювання попередніх чарунок. В результаті отримаємо таку таблицю:

	A	B	C	D
1	0	1	0,5	0,914214
2	0	0,5	0,25	-0,56079
3	0,25	0,5	0,375	0,17184
4	0,25	0,375	0,3125	-0,19564
5	0,3125	0,375	0,34375	-0,0122
6	0,34375	0,375	0,359375	0,079745
7	0,34375	0,359375	0,351563	0,033754
8	0,34375	0,351563	0,347656	0,010773
9	0,34375	0,347656	0,345703	-0,00071
10	0,345703	0,347656	0,34668	0,005029
11	0,345703	0,34668	0,346191	0,002157
12	0,345703	0,346191	0,345947	0,000722
13	0,345703	0,345947	0,345825	3,67E-06
14	0,345703	0,345825	0,345764	-0,00036
15	0,345764	0,345825	0,345795	-0,00018
16	0,345795	0,345825	0,34581	-8,6E-05
17	0,34581	0,345825	0,345818	-4,1E-05
18	0,345818	0,345825	0,345821	-1,9E-05
19	0,345821	0,345825	0,345823	-7,5E-06
20	0,345823	0,345825	0,345824	-1,9E-06
21	0,345824	0,345825	0,345825	8,66E-07
22	0,345824	0,345825	0,345824	-5,4E-07
23	0,345824	0,345825	0,345825	1,65E-07
24	0,345824	0,345825	0,345825	-1,9E-07
25	0,345825	0,345825	0,345825	-1E-08

Як бачимо, починаючи з рядка 23 у стовбці С зміна значень припиняється. Це ефект обчислювальної похибки, який докладніше розглянутий у лекції далі. Насправді досягнуто найбільш точне значення кореня, яке взагалі можливе при даному форматі чарунку, тобто при даному числі значущих цифр. У стовбці D відповідні значення f(x) вкрай близькі до нуля (наприклад у рядку 25 -1E-08 – це –10^-8). Якщо розширити стовбець С, то число значущих цифр зросте і зміна значень продовжиться. Проте при заданій точності  = 0.5*10^-5 це число є достатнім. Перевіримо правильність отриманого розв’язку безпосередньо. А саме задамо у чарунку С26 формулу = С25 + 0,5*10^-5, у чарунку С27 формулу = С25 – 0,5*10^-5. В результаті отримаємо:

	A	B	C	D
23	0,345824	0,345825	0,345825	1,65E-07
24	0,345824	0,345825	0,345825	-1,9E-07
25	0,345825	0,345825	0,345825	-1E-08
26			0,34583	2,94E-05
27			0,34582	-2,9E-05

Значення f(x) у стовбці D підраховуються автоматично. Оскільки f(0,345825 + 0,5*10^-6) > 0, a f(0,345825 – 0,5*10^-6) < 0, то значення 0,345825 є коренем рівняння з точністю  = 0.5*10^-6.

Наприкінці цього розділу запитаємо, чи можливе застосування методу дихотомії на відрізку з умовою f(a)*f(b)<0, який не є відрізком ізоляції кореня? Принципово це так, алгоритм відпрацює без перешкод і корінь рівняння буде знайдений, але лише один. Для розв’язання рівняння, тобто для пошуку інших коренів на необхідно спершу застосувати процедуру відокремлення коренів до цього відрізка.