§ 6. Метод подвійного перерахунку.

Нехай залишковий член деякої узагальненої квадратурної формули Ньютона – Котеса має порядок р відносно кроку інтегрування h: R( f ) = О(h^р). Поділимо відрізок [a; b] на n рівних відрізків і на 2n рівних відрізків, нехай I_n та I_2n – відповідні наближені значення інтеграла за цією квадратурною формулою, а R_n( f ) і R_2n( f ) – відповідні залишкові члени. Метод подвійного перерахунку ґрунтується на двох формулах.

1. R2n ( f ) ≈ (правило Рунге) (14)

2. ≈ I_n,2n = I_2n + (формула екстраполяції за Річардсоном). (15)

Назва екстраполяція пов’язана з тим, що коли I_n ≠ I_2n, то уточнене значення I_n,2n ніколи не лежить між I_n та I_2n. Справді, якщо I_2n > I_n, то з (15) випливає, що I_n,2n > I_2n = max{ I_n, I_2n }. Якщо ж I_2n < I_n, то I_n,2n < I_2n = min{ I_n, I_2n }. Формул (14) і (15) достатньо для практичної реалізації методу подвійного перерахунку (див. наступний параграф). Тут далі наведені обґрунтування цих формул і водночас їх точне формулювання. Функцію f(х) будемо вважати диференційовною стільки разів, скільки це виявиться необхідним.

Спочатку зазначимо, що оскільки 1) завжди залишковий член квадратурної формули Ньютона – Котеса на відрізку [a; b] R( f ) = , де R_m( f, х) = f(х) – L_m(x) – це залишковий член відповідної інтерполяційної формули, а 2) згідно з теоремою 1 розділу R_m( f, х) = ω_m+1(х), де ξ = ξ(x) є [a; b], то і R( f ) = , де ξ  [a; b]. Справді, оскільки ≤ R( f ) ≤ , а функція f^(m+1)(x) неперервна, то для деякого ξ  [a; b] R( f ) = f^(m+1)( ξ) ,

R( f ) = f^(m+1)(ξ) = f^(m+1)(ξ) h^m+2, (16)

де h = b – a – довжина відрізку, а – стала. Тут = , х = + t , х_j = + d_j (j = 0, 1, … , m). Очевидно, порядок R( f ) згідно (16) дорівнює m + 2. Формулу (16) використаємо для обґрунтування (14) і (15), до чого й переходимо безпосередньо.

Нехай задана деяка узагальнена квадратурна формула Ньютона – Котеса порядку р відносно кроку інтегрування h: R( f ) = О(h^р). Поділимо відрізок [a; b] на n рівних відрізків завдовжки h = (b – a)/n точками a = х₀ < х₁ < … < х_k < … < х_n = b і на 2n рівних відрізків завдовжки h/2 = (b – a)/2n точками a = y₀ < y₁ < … < y_k < … < y_2n = b так, щоби х_k = y_2k (k = 0, 1, …, n). За означенням узагальненої квадратурної формули до кожного з відрізків [х_k; х_k+1] застосуємо дану неузагальнену формулу Ньютона – Котеса і отримаємо відповідні наближені значення I_nk інтеграла та залишкові члени R_nk( f ). Згідно з висновком § 5 R_nk( f ) = О(h^р+1), згідно з (16) R_nk( f ) = f^(m+1)(ξ_nk) h^m+2, де ξ_nk  [х_k; х_k+1], звідки p = m + 1. За побудовою на кожному відрізку [х_k; х_k+1] розташовані два відрізка: [у_2k; у_2k+1] та [у_2k+1; у_2k+2] (бо х_k = у_2k, х_k+1 = у_2k+2). Аналогічно дістанемо на кожному з цих відрізків наближені значення I_2n2k інтегр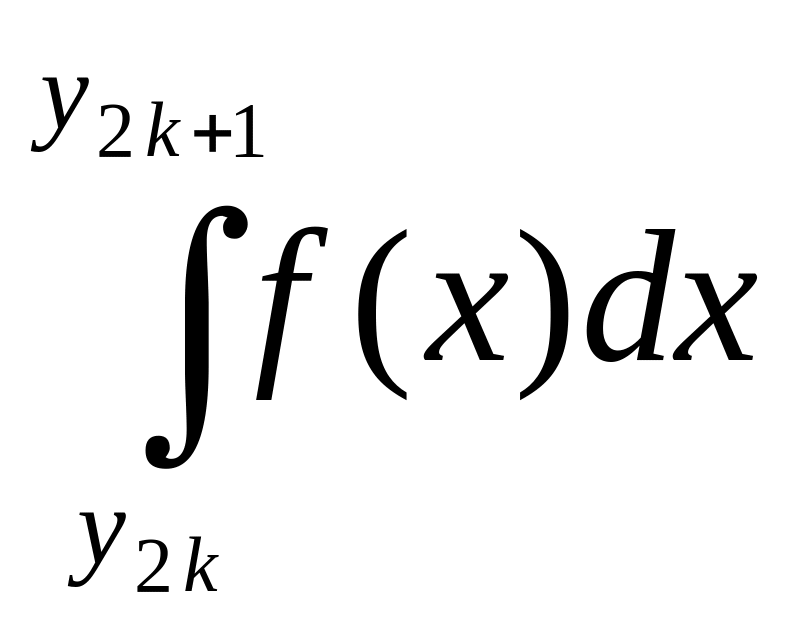ала та I_2n2k+1 інтеграла і відповідні залишкові члени R_2n2k( f ) та R_2n2k+1( f ): R_2n2k( f ) = О( )^p+1 , R_2n2k+1( f ) = О( )^p+1 , R_2n2k( f ) = f^(m+1)(ξ_2n2k) ( )^p+1, R_2n2k+1( f ) = f^(m+1)(ξ_2n2k+1) ( )^p+1, оскільки р + 1 = m + 2 (ξ_2n2k  [у_2k; у_2k+1], ξ_2n2k+1  [у_2k+1; у_2k+2]) . Отже, інтеграл I_k = = I_nk + R_nk( f ) = I_nk + М_nk h^р+1, де М_nk = f^(m+1)(ξ_nk). Але = = 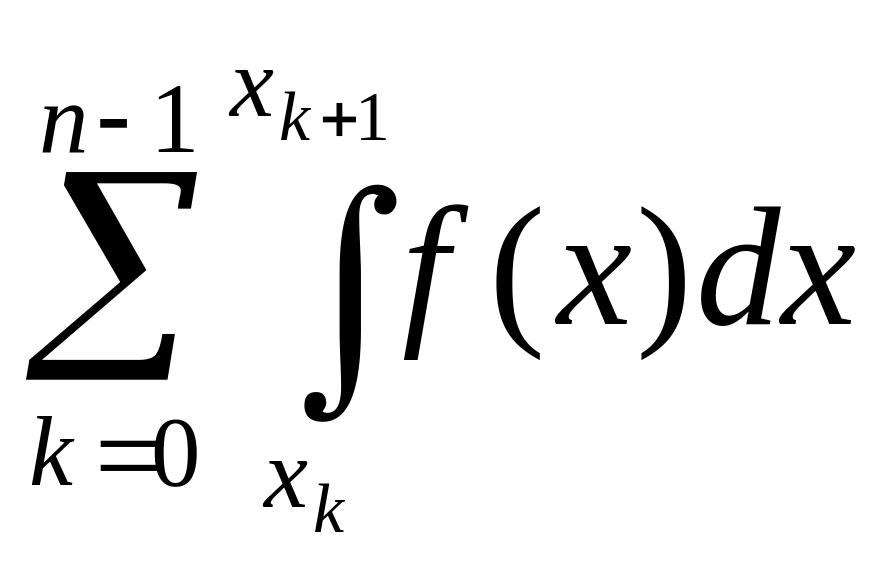= I , а за означенням узагальненої квадратурної формули = I_n, = R_n( f ) = ∙ h^р+1. Тому I = = + = I_n + R_n( f ) = I_n + ∙ h^р+1. З іншого боку, I_k = = + = (I_2n2k + R_2n2k( f )) + (I_2n2k+1 + R_2n2k+1( f )) = (I_2n2k + I_2n2k+1) + (R_2n2k( f ) + R_2n2k+1( f )) = (I_2n2k + I_2n2k+1) + (М_2n2k + М_2n2k+1) ∙ ( )^p+1, де М_2n2k = f^(m+1)(ξ_2n2k), М_2n2k+1 = f^(m+1)(ξ_2n2k+1). Але за означенням узагальненої квадратурної формули = I_2n, = R_2n( f ) = ∙ ( )^p+1. Тому з іншого боку I = = + = I_2n + R_2n( f ) = I_2n + ∙ ( )^p+1. Отже,

I = I_n + R_n( f ) = I_n + ∙ h^р+1 . (17)

I = I_2n + R_2n( f ) = I_2n + ∙ ( )^p+1 . (18)

Спочатку при кожному k знехтуємо відмінністю між М_nk, М_2n2k і М_2n2k+1 – значеннями функції f^(m+1)(х) на відрізку [х_k; х_k+1] довжини h  0 і покладемо М_nk ≈ М_2n2k ≈ М_2n2k+1 ≈ М_k, М = , С = M h. В такому разі отримуємо

I = I_n + R_n( f ) = I_n + M h^р+1 = I_n + Сh^р ,

I = I_2n + R_2n( f ) = I_2n + 2M ( )^p+1 = I_2n + С( )^p . (19)

Відомими в (19) є I_n , I_2n , h і р, невідомими I та С. Отже, це система двох лінійних рівнянь з двома невідомими. Звідси I_2n + С( )^p – (I_n + Сh^р) = 0 ; I_2n – I_n = Сh^р – С( )^p = С( )^p(2^р – 1) = R_2n( f )(2^р – 1) , звідки знаходимо R_2n( f ) = (правило Рунге). Тому I = I_2n + R_2n( f ) = I_2n + (формула екстраполяції за Річардсоном). Це точні

формули, єдине неточне припущення у доведенні – рівність М_nk ≈ М_2n2k ≈ М_2n2k+1 ≈ М_k . Отже, покладемо М_k = М_nk, Δ_2n2k = М_2n2k – М_k = f^(m+1)(ξ_2n2k) – f^(m+1)(ξ_nk) = f^(m+2)(η_2n2k) ∙ (ξ_2n2k – ξ_nk), де за теоремою Лагранжа η_2n2k  [ξ_2n2k; ξ_nk]  [х_k; х_k+1], звідки Δ_2n2k ≤ ∙h. Аналогічно Δ_2n2k+1 = М_2n2k+1 – М_k = f^(m+1)(ξ_2n2k+1) – f^(m+1)(ξ_nk), звідки за

теоремою Лагранжа Δ_2n2k ≤ ∙ h. Таким чином = 2 + = 2М + Δ, де Δ = , Δ ≤ 2n ∙h = 2 (b – a). Отже, точний варіант (19), що випливає з (17), (18) це

I = I_n + R_n( f ) = I_n + M h^р+1 = I_n + Сh^р ,

I = I_2n + R_2n( f ) = I_2n + (2M + Δ) ( )^p+1 = I_2n + С( )^p + B( )^p+1 (B = Δ ). (20)

Як і раніше, звідси I_2n + С( )^p + B( )^p+1 – (I_n + Сh^р) = 0 ; I_2n – I_n = Сh^р – С( )^p – B( )^p+1 = С( )^p(2^р – 1) – B( )^p+1 = R_2n( f )(2^р – 1) – (2^р – 2)B( )^p+1, звідки знаходимо = R_2n( f ) – B( )^p+1. Отже, значення відрізняється від R_2n( f ) на величину B( )^p+1 порядку р + 1 відносно h, тобто на одиницю більшу порядку R_2n( f ). Тому і величина I_n,2n = I_2n + з формули екстраполяції за Річардсоном (15) насправді відрізняється від точного значення інтеграла І = на ту ж величину B( )^p+1 порядку р + 1, яку природно позначити R_n,2n( f ). Отже, точні варіанти (14) і (15) це

1. R_2n ( f ) = + О(h^p+1), 2. = I_n,2n + R_n,2n( f ) = I_2n + + О(h^p+1).

Поділимо відрізок [a; b] на n, на 2n і на 4n рівних відрізків, дістанемо I_n,2n і аналогічно I_2n,4n : = I_n,2n + R_n,2n( f ) = I_2n,4n + R_2n,4n ( f ), де R_n,2n( f ) = О(h^p+1), R_2n,4n ( f ) = О( )^p+1 . Так само, як і вище, можна довести, що величина = R_2n,4n ( f ) + О(h^p+2), тобто відрізняється від R_2n,4n ( f ) на величину порядку на одиницю більшу за порядок R_2n,4n ( f ). Звідси = I_2n,4n + + О(h^p+2), тобто отримуємо вже наближення порядку р + 2. Процес можна продовжити і далі, отримуючи наближення порядку р + 3, р + 4, … . Доведення такого методу кратного перерахунку по суті повторює наведене вище, хоча потребує ще більшої кількості позначень. Реалізацію цього метода за допомогою Excel розглянемо у наступному параграфі.