Задание на лабораторную работу

1. В среде MATHCAD ввести два вектора (значения элементов выбираются самостоятельно). С введенными векторами произвести операции:

• сложения;

• скалярного и векторного умножения;

• умножения вектора на число.

2. Ввести матрицу размерностью 55 (значения элементов выбираются самостоятельно) или же сформировать матрицу по определенному Вами алгоритму, при этом желательно использовать функцию задания случайного среднего.

Найти:

• максимальный и минимальный элементы;

• число элементов в матрице;

• определитель (determinant);

• значение элемента в 3–й строке, 2-м столбце;

• сумму диагональных элементов;

• упорядочить третий столбец матрицы по возрастанию;

• произвести операцию векторизации и найти такую матрицу, каждый элемент которой определяется тангенсом от элемента предыдущей матрицы.

3. Сформировать матрицу, состоящую из двух столбцов, согласно следующему алгоритму:

• в первый столбец записать значения вещественной части выражения 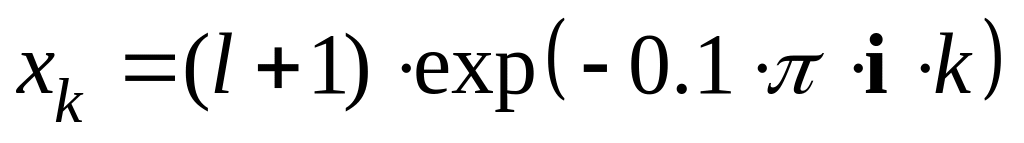, (i – мнимая единица, k – дискретная переменная, изменяющаяся от нуля до 30, l – последняя цифра номера зачетной книжки);

• во второй столбец – значения мнимой части выражения – 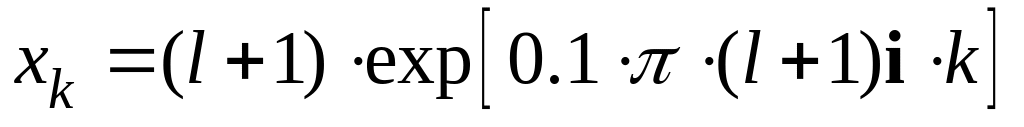(обозначения те же);

• Построить график зависимости элементов второго столбца от первого.

Вопросы для самоконтроля

1. Какие виды массивов в MathCAD Вам известны?

2. Какая системная переменная определяет нижнюю границу индексации элементов массива?

3. Опишите способы создания массивов в MathCAD.

4. Как просмотреть содержимое массива, определенного через дискретный аргумент?

5. Как построить график функции, которая задана в матричной форме?

6. В чем заключается применение операции векторизации к матрице?

7. Какие операции с матрицами и векторами Вам известны?

8. Каков физический смысл операции, выполняемой в п.3 задния лабораторной работы?

Лабораторная работа №3 Решение систем уравнений Цель работы

Ознакомиться с основными методами решения систем уравнений и реализацией их в пакете MathCAD.

Методические указания

Способы решения систем уравнений делятся на две группы:

• точные методы, представляющие собой конечные алгоритмы для вычисления корней системы. Они пригодны для решения систем линейных уравнений. К ним относятся решение с помощью обратной матрицы, методы Крамера (для отыскания единственного решения системы), Гаусса (метод позволяющий находить решение уравнений даже в случае, если оно не является единственным) и др.;

• приближенные методы, позволяющие получить решение системы с заданной точностью путем сходящихся итерационных процессов (последовательных приближений). Они пригодны для решения как линейных, так и нелинейных уравнений.

Точные методы решения систем линейных уравнений

Рассмотрим систему n линейных алгебраических уравнений относительно неизвестных х₁, х₂, …, х_n:

(3.1)

В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в матричной форме:

Ах = b, (3.2)

где:

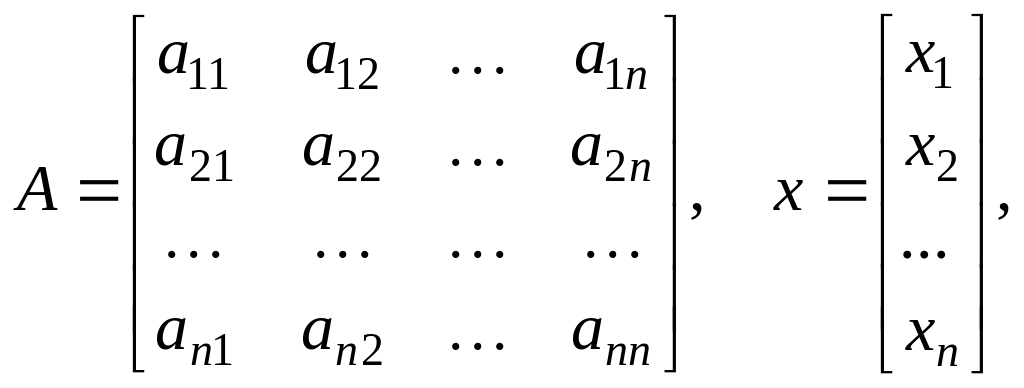
. (3.3)

Матрица А называется матрицей системы, матрица-столбец b – матрицей правой части, а матрица-столбец х, – решением системы. Очевидно, что число строк квадратной матрицы A и вектора b должно совпадать.

Если матрица А является невырожденной (det A  0), то существует обратная матрица А^-1 и, умножая обе части уравнения (3.3) на неё, получим выражение для решения системы, которое является единственным:

(3.4)

Пакет MathCAD позволяет сформировать обратную матрицу и получить решение (3.4) непосредственно, а также, используя для этой цели встроенную функцию lsolve (A,b).

Альтернативным способом решения системы уравнений является метод Гауссовых исключений. Он состоит в том, что систему (3.1) приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей:

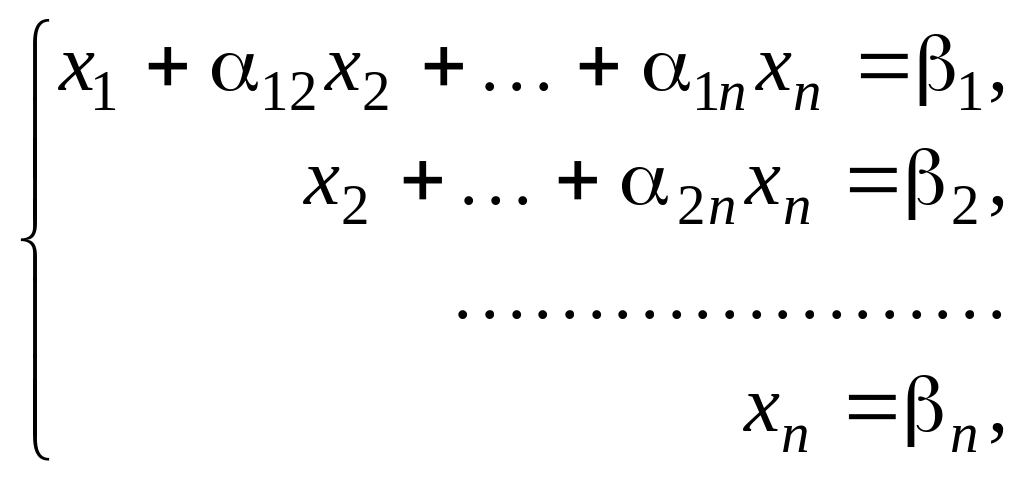(3.5)

решение которой может быть найдено по рекуррентным формулам:

(3.6)

В матричной записи метод Гаусса сводится к преобразованию расширенной матрицы C эквивалентной системы (объединение матрицы системы и вектора правой части) к такому виду, чтобы в первых n столбцах получилась единичная матрица, тогда последний, (n + 1) столбец этой матрицы и будет содержать решение системы (3.1). В MathCAD’е формирование расширенной матрицы С производится с помощью встроенной функции augment (A,b) (число строк у A и b должно совпадать), а процедуру ее преобразования (т.н. прямой и обратный ходы метода Гаусса) выполняет встроенная функция rref(С). Затем вектор решения можно выделить как последний столбец преобразованной матрицы. Приведем примеры точного решения системы линейных уравнений различными методами:

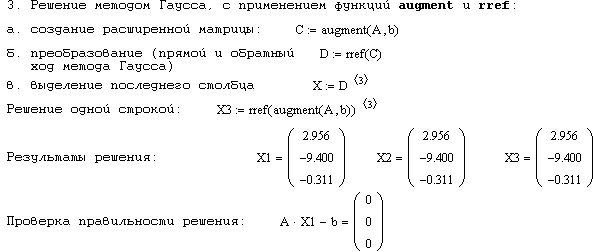
Часто символьная (аналитическая) форма решения уравнений оказывается более удобной для анализа результатов. Так, например, решение в символьном виде может выразить корни через параметры, входящие в уравнения системы и вместо того, чтобы решать уравнение для каждого нового значения параметра, можно просто заменять его значение в найденном символьном решении.

Решение в символьном виде выполняется внутри блока решений, который открывается ключевым словом Given. Ниже его в любом порядке печатаются уравнения, причем для ввода знака = используется [Ctrl]=. Завершает блок функция Find, аргументами которой являются искомые переменные, входящие в состав системы. Для того, чтобы эта функция возвратила аналитическое решение системы уравнений необходимо поместить за ней символьный знак равенства , который набирается с помощью меню Символы (Symbolic) или комбинацией клавиш [Ctrl] . Внутри блока решения выражения недопустимы – ограничения со знаком ; дискретный аргумент или выражения, содержащие дискретный аргумент в любой форме; неравенства вида a < b < c. Блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find. Пример символьного решения системы уравнений представлен в следующем MathCAD документе:

Приближенные методы решения систем уравнений

Вследствие неизбежных округлений результаты даже точных методов являются приближенными, а при использовании приближенных методов, сверх того, добавляется погрешность метода. Тем не менее, иногда приближенные методы представляются более удобными. Так, если линейная система высокого порядка имеет достаточно разреженную главную матрицу А (многие из ее элементов вдали от главной диагонали равны нулю или же диагональные элементы значительно преобладают над остальными) применение итерационных методов представляется предпочтительным. Поскольку системы нелинейных уравнений редко могут быть решены точно, то в этом случае итерационные методы являются единственно приемлемыми.

Максимальное число уравнений (и переменных), допускающих использование итерационных методов равно 50. Приближенное решение ищется внутри блока решений, только перед ключевым словом Given следует задать начальное приближение для всех неизвестных, входящих в систему, а для вывода на экран решения после функции Find (с аргументами в виде искомых переменных) ставится обычный, а не символический знак равенства.

Алгоритм применения функции Find включает возможность выбора соответствующего способа решения из группы имеющихся итерационных методов¹, а, кроме того, при наличии дополнительных пакетов расширения MathCAD функция она позволяют решать задачи смешанного и целочисленного программирования.

Ниже приведен пример MathCAD документа, в котором реализован приближенный (итерационный) метод решения систем уравнений:

Функция Find, завершающая блок решения, может быть использована аналогично любой другой функции. Так, в частности, допустимо:

• Вывести найденное решение, напечатав выражение вида: Find(x,y,…) =;

• При необходимости использовать решение системы уравнений в другом месте рабочего документа можно определить новую переменную a := Find(x) – скаляр, или b := Find(x,y,…) – вектор;

• Если необходимо многократно решать систему уравнений для различных значений некоторых параметров a, b, c,…то можно определить новую функцию выражением: f(a, b, c, …) := Find(x, y, z, …).

В ряде случаев система может выдавать сообщение об ошибке (решение не найдено):

Это возможно, если: систем не имеет решений, неправильно выбрано начальное приближение (например, вещественное число, а система имеет комплексные корни) или, если последовательность приближений попала в точку локального минимума невязки (отклонения приближенного решения от истинного). Возможно также, что, поставленная задача не может быть решена с заданной точностью – тогда необходимо изменить значение системной переменной TOL.

Примечание 1. Функция Minerr очень похожа на функцию Find и имеет те же правила использования. Однако, поскольку она является более отработанной, «заслуженной» и надежной функцией, то, если в результате поиска не может быть получено дальнейшее уточнение текущего приближения к решению, Minerr возвращает это приближение, в отличие от функции Find, которая в этом случае выдает сообщение об ошибке.

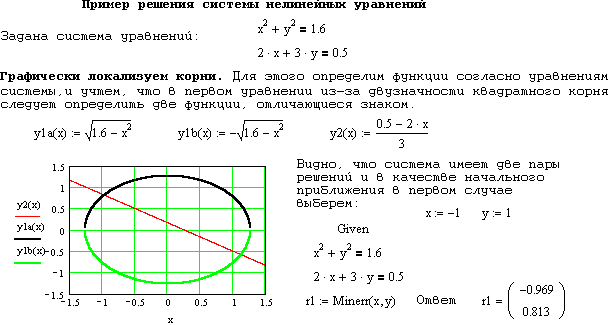
Примечание 2. Если при решении систем линейных уравнений удачный выбор начального приближения определяет эффективность применения приближенного метода, то в случае нелинейных систем решений может быть несколько, поэтому сами значения получаемых результатов могут сильно зависеть от выбора начального приближения. Поэтому рекомендуется до решения графически локализовать значения корней. Для этого нелинейные уравнения преобразуются к виду y=f₁(x) и y=f₂ (x) и определяют начальное приближение по точке пересечения этих графиков. Пример решения системы нелинейных уравнений: