Лабораторная работа № 2 Работа с векторами и матрицами в системе mathcad Цель работы

Ознакомление с правилами формирования и преобразования матриц, основными действиями над ними.

Методические указания

Массив – представляет собой совокупность некоторого конечного числа числовых или символьных элементов, упорядоченных некоторым образом, которая имеет уникальное имя. В пакете MathCAD используются массивы двух наиболее распространенных типов:

• одномерные (векторы);

• двумерные (матрицы).

Порядковый номер элемента, который является его адресом, называется индексом. Индексы могут иметь только целочисленные значения. Они могут начинаться с нуля или единицы, в соответствии со значением системной переменной ORIGIN (которая по умолчанию считается равной нулю).

Векторы и матрицы можно задавать различными способами:

• с помощью команды Вставка (Insert) Матрица (Matrices) из меню Math, или комбинации клавиш Ctrl + M, или щелчком на кнопке панели Матрица, заполнив массив пустых полей для не слишком больших массивов. Отметим, что ввод за переменной ее индекса также допустим двумя способами: нажатием на панели математических инструментов на кнопку-иероглиф «Переменная с индексом» или набором за именем переменной символа открывающихся квадратных скобок (рудимент языков Pascal и C, где квадратные скобки означают индексную переменную).

• с использованием дискретного аргумента, когда имеется некоторая явная зависимость для вычисления элементов через их индексы.

• импортируя данные из структурированного ASCII-файла используя выражение X:=READPRN(имя файла). Последнее часто бывает необходимо, если исследуемая техническая система или экспериментальная установка оборудована средствами АСНИ (автоматизированная система научных исследований) и данные с приборов заносятся на магнитный диск.

Рассмотренные способы ввода отражены в следующем MathCAD-документе:

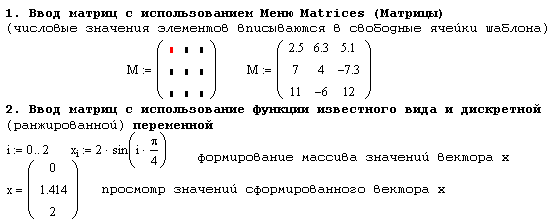
Пакет MathCAD позволяет производить алгебраические процедуры с матрицами, векторами и скалярами, а также преобразовывать их по определенным правилам.

Некоторые другие встроенные векторные и матричные функции, облегчающие решение задач линейной алгебры и других сфер приложения векторов и матриц приведены в табл. 3 (использованы условные обозначения вектор – V, матрица – М, скаляр – Z).

Любое вычисление, которое MathCAD может выполнить с одиночными значениями, он может выполнять с векторами и матрицами. Это можно реализовать двумя способами: последовательно выполняя действия над каждым элементом массива и используя оператор векторизации. Для ввода этого оператора необходимо выделить объект и нажать одновременно клавиши [ Ctrl ] и "Минус" или использовать соответствующий пункт меню Матрицы.

Таблица 3.

Название функции	Действие функции
length(V)	- возвращает число элементов вектора
last(V)	- возвращает индекс последнего элемента
colsM)	- возвращает число столбцов матрицы
rows(M)	- возвращает число строк матрицы
Re(V) или Re(M)	- возвращает вектор (или матрицу) действительных частей вектора с комплексными элементами
Im(V) или Im(M)	- возвращает вектор мнимых частей вектора (или матрицы) с комплексными элементами
identity(n)	- создает единичную квадратную матрицу размером n*n
submatrix(A,ir,jr,ic,jc)	- возвращает субматрицу, состоящую из всех элементов, содержащихся в строках от ir по jr и столбцов с ic по jc (jrir, jcic)
diag(V)	- создает диагональную квадратную матрицу, элементы главной диагонали которой совпадают с элементами вектора V

Оператор векторизации меняет смысл операций. Например, пусть Q некоторая матрица. Тогда запись exp(Q) или (в среде MathCAD) является некорректной, так как аргументом функции exp (или радикал) должна быть простая переменная, а не матрица. Применение к этой функции оператора векторизации приводит к вычислению функции от каждого элемента матрицы и результатом также является матрица. Это иллюстрирует фрагмент следующего документа:

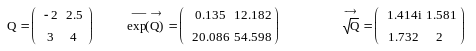
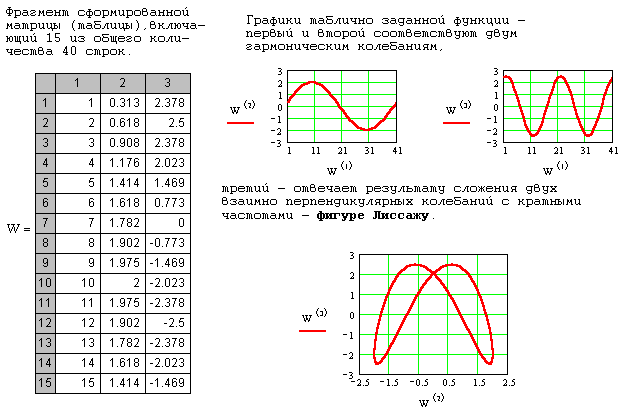
Если результаты экспериментальных наблюдений или расчетов формируют матрицы, то имеется возможность строить графики (как обычные, так и трехмерные) функций, заданных в виде таблиц. При этом в качестве независимого аргумента (и зависимой переменной) может быть выбран любой из столбцов (или любая из строк) данной матрицы. Пример построения графика по имеющейся таблице приведен в следующем документе: