
- •Темы и объем лабораторных занятий (академические часы)
- •Введение
- •Лабораторная работа №1 Основы работы с MathCad Цель работы
- •Методические указания
- •Операторы
- •Типы данных
- •Функции
- •Текстовые фрагменты
- •Графические области
- •2. Traces (след) – управляет параметрами линий, которыми строится график
- •3. Labels (метки) – установка надписей по осям и титульной надписи
- •4. Defaults (умолчание) – задание режима по умолчанию
- •Порядок выполнения лабораторной работы
- •Вопросы для самоконтроля
- •Лабораторная работа № 2 Работа с векторами и матрицами в системе mathcad Цель работы
- •Методические указания
- •Задание на лабораторную работу
- •Вопросы для самоконтроля
- •Лабораторная работа №3 Решение систем уравнений Цель работы
- •Методические указания
- •Задание на лабораторную работу
- •Вопросы для самоконтроля
- •Лабораторная работа №4 Решение нелинейных уравнений Цель работы
- •Методические указания
- •Метод половинного деления
- •Метод хорд
- •Метод Ньютона
- •Метод простой итерации (последовательных итераций)
- •Задание на лабораторную работу
- •Вопросы для самоконтроля
- •Лабораторная работа №5 Интерполяция функций Цель работы
- •Методические указания
- •Задание к лабораторной работе
- •Вопросы для самоконтроля
- •Лабораторная работа № 6 Аппроксимация функций. Построение регрессионных зависимостей методом наименьших квадратов. Цель работы
- •Методические указания
- •Задание к лабораторной работе
- •Вопросы для самоконтроля
- •Лабораторная работа №7 Основы программирования в пакете MathCad Цель работы
- •Методические указания
- •Задание на лабораторную работу
- •Задание к лабораторной работе
- •Вопросы для самоконтроля
- •Лабораторная работа № 9 Решение дифференциальных уравнений методом символьного интегрирования Цель работы
- •Методические указания
- •Задание на лабораторную работу
- •Вопросы для самоконтроля
- •Задание к лабораторной работе
- •Вопросы для самоконтроля
- •Задание на лабораторную работу
- •1. Цель курсовой работы
- •2. Введение
- •3. Аналитические методы
- •3.1 Классический метод
- •3.2. Метод операционного исчисления
- •4. Численный метод решения дифференциальных уравнений
- •5. Задание на курсовую работу
- •5.1. Выбор варианта
- •5.2. Порядок действий
- •Требования к пояснительной записке:
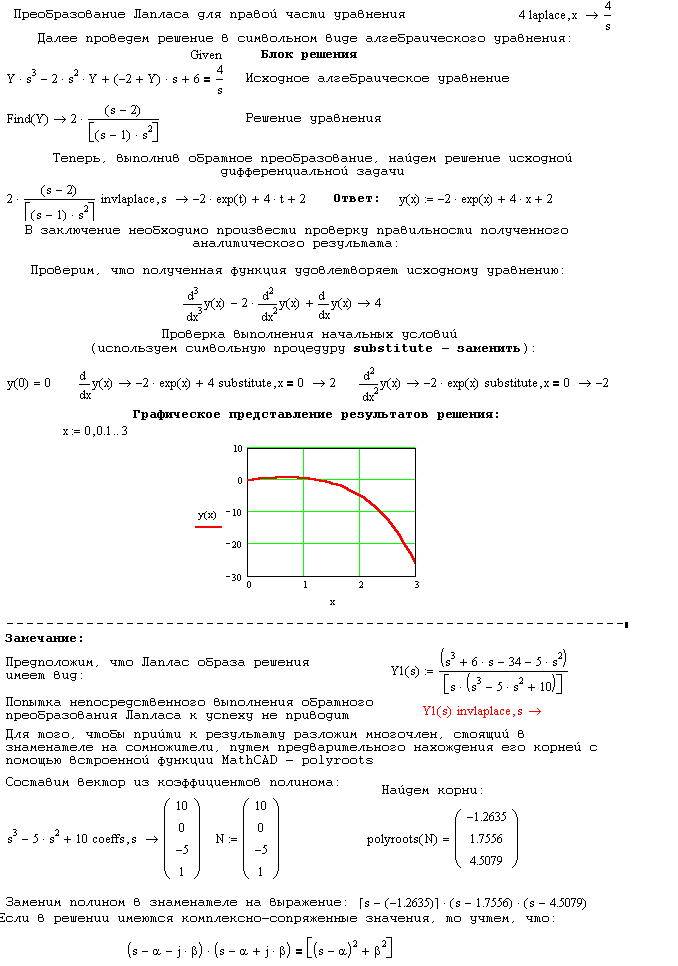
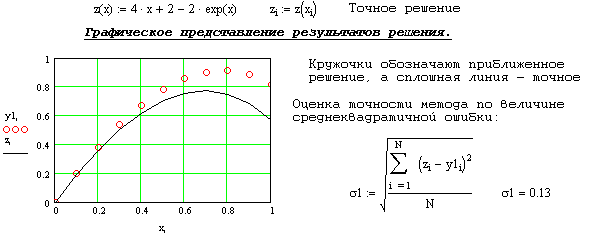
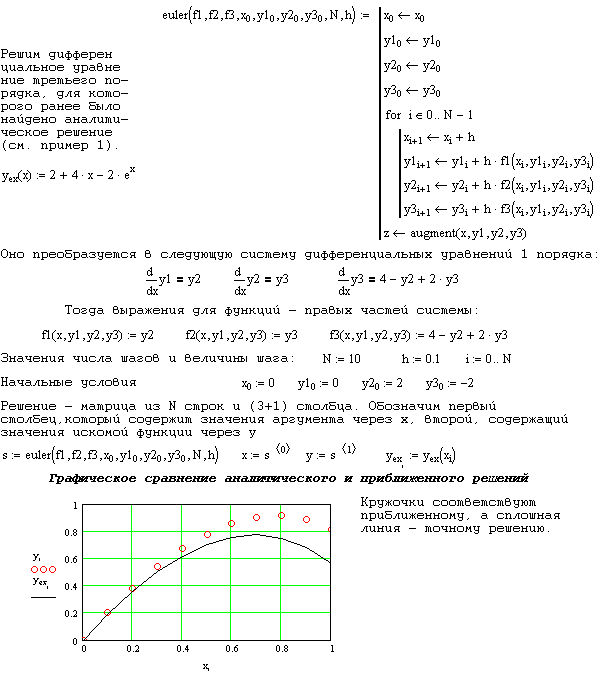
- •Приложение: Примеры выполнения этапов курсовой работы
- •Рекомендуемая литература.
- •65029. Одесса-29, Дидрихсона, 8.
Требования к пояснительной записке:
Пояснительная записка должна содержать:
Титульный лист, оформленный в соответствии с требованиями стандарта ОНМА.
Условие задания.
Краткое описание используемых численных и аналитических методов решения задачи.
Приведение заданных уравнений к системе дифференциальных уравнений первого порядка.
Описание реализации выбранных алгоритмов расчета и их представление в среде MathCAD.
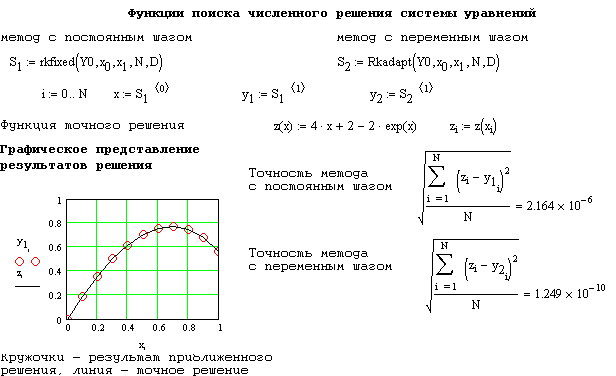
Результат исследования влияния величины шага h на точность решения.
Результаты решения, представленные в виде таблиц значений функций и графиков. Графики должны быть правильно отформатированы (правильно выбран масштаб по осям, нанесена сетка вспомогательных линий, толщина и способ передачи линий и точек адаптирован к условиям черно-белой печати).
Оценку точности полученных результатов.
Текст работы должен быть представлен на листах формата А4. Рекомендуется выполнить компьютерный набор всего текста в текстовом редакторе, однако допускается и рукописный вариант. В любом случае необходимо выполнить распечатку всех созданных MathCAD документов (Work sheets), снабженных текстовыми комментариями выполненных действий.
Список использованной литературы.
Приложение: Примеры выполнения этапов курсовой работы

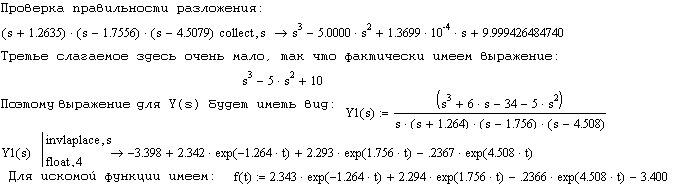



Рекомендуемая литература.
Дьяконов В. П. MATHCAD 2000: Учебный курс. СПб.: Питер, 2001. – 592 с.
Дьяконов В.П., Авраменкова И.В. MathCAD 8 PRO в математике, физике и Internet. М.: Нолидж, 1999. – 512 с.
Методи обчислень: Практикум на ЕОМ: Навчальний посібник. – К.: Вища школа, 1995. – 303 с.
Очков В. Ф.. MathCAD 8 PRO для студентов и инженеров. М.: КомпьютерПресс, 1999. – 593 с.
Плис А. И., Сливина Н. А. MathCAD. Математический практикум. М.: Финансы и статистика, 1999. – 656 с.
Херхагер М., Партоль Х.. MathCAD 2000. Полное руководство. «Ирина», BHV, Киев, 2000. – 416 с.
Учебное издание
Поповский Алексей Юрьевич, Брошков Сергей Дмитриевич
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ В СРЕДЕ MATHCAD
Подписано к печати 24.04.03. Формат 60Х84/16. Бумага офсетная.
Усл. печ. л. 4,3.
Тираж 50 экземпляров. Заказ №________.
ОНМА, центр "ИздатИнформ"
Свидетельство ДК №1292 от 20.03.2003
65029. Одесса-29, Дидрихсона, 8.
тел./факс: (0482) 34-14-12
publish@ma.odessa.ua
1 Разработан целый ряд приближенных методов – простой итерационный, модифицированный итерационный (Зейделя) – для решения линейных систем; квазиНьютона, сопряженных градиентов, Левенберга – Марквардта для решения нелинейных систем.
2 Критерии близости функций (x) и f(x) могут быть различными.
3 Следует иметь в виду, что точность экстраполяции обычно невелика.
4 хотя можно, вообще говоря, решать и задачу экстраполяции назад.
5 Заметим, что аппроксимирующая кривая фактически является линией сглаживающей экспериментальные точки.
6 Допустимо обратиться за консультацией к преподавателю.
7 У алхимиков есть символ «Змея, глотающая свой хвост», который подходит и для рекурсии, – маленькая программа, заглатывающая память компьютера.
8 Здесь и далее под у.е. понимаются именно условные единицы, а не доллары.
9 За кормовую единицу принимают питательность 1 кг сухого овса, имеющий питательность 1414 ккал.
