Задание к лабораторной работе
В соответствии с дифференциальным уравнением своего варианта из лабораторной работы №8 необходимо произвести расчет решения методами Эйлера и Рунге-Кутта, выбирая различную величину шага h. При этом один из методов реализовать в матричной форме, а другой с помощью программы-функции. Результат сравнить с аналитическим решением, полученным в предыдущей работе. Сравнение провести в табличной или графической формах и оценить погрешность.
Пример 1
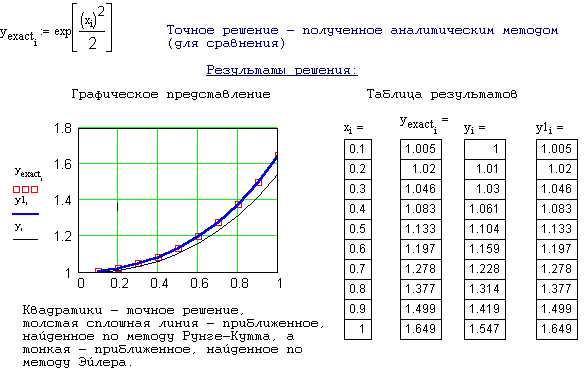
Пример 2.
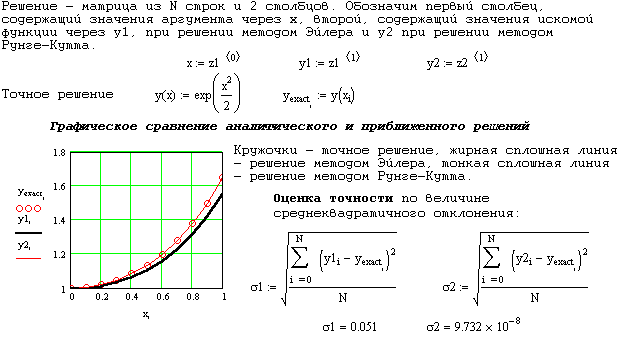
Вопросы для самоконтроля
В чем заключаются преимущества приближенных численных методов решения дифференциальных уравнений?
Какова идея и геометрическая интерпретация метода ломаных Эйлера?
Как можно запрограммировать алгоритм этого метода?
Каковы преимущества и недостатки метода Эйлера?
В чем заключается метод Рунге-Кутта 4 порядка? Какова его точность?
Какова геометрическая интерпретация метода Рунге-Кутта?
Лабораторная работа № 11
Решение задач линейного программирования
Цель работы
Ознакомиться с классом задач, решаемых методом линейного программирования, научиться составлять выражения для целевой функции и использовать возможности пакета MathCAD для нахождения ее экстремума.
Методические указания
Имеется широкий (и жизненно важный) класс задач, в которых приходится что-то оптимизировать (расходы, прибыль, наибольший объем продукции, минимальные издержки производства), при этом необходимо учитывать ограничения (доходы, дефицитность ресурсов – машин, людей, сырья, топлива, зарплаты). Приведем следующий пример:
После часа пик (зимнее утро, к примеру) расход электроэнергии падает и необходимо снижать нагрузку электрогенераторов. Как это делать? Можно отключить отдельные турбогенераторы, а можно оставить их в работе, изменив нагрузку. Диспетчер энергосистемы дает соответствующие команды, ориентируясь на средний расход топлива по системе, выброс с дымовыми газами вредных веществ в атмосферу, износ оборудования, степень готовности электростанций и дальше менять нагрузку и т.д. Переменные такой оптимизации могут быть и вещественными (мощность отдельного энергоблока, которая меняется, естественно, в разумных пределах, определяемых техническими условиями – ограничения в задаче) и целочисленными (число работающих блоков).
В задачах данного типа важно составить математическую модель рассматриваемой проблемы и выразить качество использования ресурсов с помощью функции нескольких переменных, которая называется целевой функцией.
Для нахождения оптимального результата требуется осуществлять поиск экстремума целевой функции при ограничениях, наложенных на ее переменные.
В случае, если и целевая функция и ограничения представлены линейными зависимостями, то такой класс задач получил название задач линейного программирования.
Рассмотрим пример составления целевой функции и решения задачи линейного программирования.
Пусть судно имеет грузоподъемность 12 тыс. т и вместимость 20 тыс. м3. Для перевозки предложено 4 типа грузов, характеристики которых приведены в табл. 13.
Таблица 13.
Код груза |
Погрузочный объем, м3/т |
Фрахтовые ставки на перевозку, у.е./т8 |
1 |
1.4 |
13.5 |
2 |
1.6 |
16.0 |
3 |
1.9 |
18.0 |
4 |
2.3 |
21.0 |
По своим техническим характеристикам судно может перевозить грузы 1 и 3 суммарным объемом не более 12 тыс. м3, а грузы 2 и 4 – суммарным объемом не более 15 тыс. м3. Также задана обязательная минимальная перевозка груза типа 4 в количестве 3 тыс. т.
Требуется составить план загрузки судна (количество груза для перевозки), обеспечивающий максимальные доходы судовладельцу, а также определить рейсовые доходы.
Математическая модель задачи и ее решение проведено в следующем MathCAD документе:
Отметим, что:
Решение задачи может зависеть от выбора начального приближения;
Применяя процедуру Maximize (Minimize) не удается решить задачу целочисленного линейного программирования, поэтому, если оптимальные значения должны быть целыми числами необходимо или использовать иной алгоритм или округлять полученные оптимальные значения компонентов до целых чисел.
Одним из вариантов задачи линейного программирования является транспортная задача. Имеется ряд пунктов отправления, в которых сосредоточены запасы груза в заданных количествах; в каждый из пунктов назначения должно быть доставлено груза в известных количествах. Требуется составить такой план перевозок, которому бы соответствовали минимальные суммарные транспортные издержки. Замена неравенств в ограничениях на равенства приводит к системе линейных алгебраических уравнений, но не с одним, а с множеством решений, одно из которых оптимизирует целевую функцию.