Вопросы для самоконтроля

1. Как составить дифференциальное уравнение, описывающее протекание во времени физического процесса в некоторой системе?

2. В чем заключается аналитический метод решения дифференциальных уравнений первого порядка в пакете MathCAD?

3. Какова последовательность операций при нахождении аналитического решения?

4. Как определить постоянную интегрирования и неизвестные коэффициенты для исследуемых моделей?

Лабораторная работа №10

Решение дифференциальных уравнений численными методами

Цель работы

Ознакомиться с основными алгоритмами численного решения простейших дифференциальных уравнений – Эйлера и Рунге-Кутта и выполнить приближенное интегрирование заданного дифференциального уравнения.

Методические указания

Далеко не всегда дифференциальное уравнение приводится к виду, допускающему разделение переменных с последующим нахождением общего интеграла в аналитической форме. Поэтому в настоящее время разработан ряд приближенных вычислительных методов, позволяющих найти решение уравнения путем построения итерационной процедуры, т.е. разбивая диапазон изменения аргумента на отрезки и вычисляя решение так, чтобы начальные условия для последующего отрезка являлись конечными значениями решения для предыдущего.

Пусть необходимо найти решение уравнения

(10.1)

с начальным условием . Такая задача называется задачей Коши. Разложим искомую функцию в ряд Тейлора вблизи точки и ограничимся первыми двумя членами разложения

.

Обозначив , получаем

(10.2)

Применяя многократно соотношение (10.2) можно находить значения функции во все новых и новых точках, т.е. аппроксимируя функцию отрезками касательной, проведенной к графику решения в начале каждого интервала. Так, двигаясь последовательно, можно приблизить искомую функцию набором коротких прямых линий, так что формула (10.2) приведет к:

(10.3)

Этот метод решения обыкновенных дифференциальных уравнений называется методом ломаных Эйлера. Он является самым простым методом, позволяющим производить вычисления без особых ухищрений и, поэтому, имеет низкую точность (первого порядка ~ h) и производительность (плата за простоту!).

Существуют различные модификации метода Эйлера, позволяющие увеличить его точность. Все они основаны на том, что производную, вычисленную в начале интервала, заменяют на среднее значение производной на данном интервале. Среднее значение производной можно получить (конечно, только приближенно) различными способами. Можно, например, оценить значение производной в середине интервала и использовать его для аппроксимации решения на всем интервале. Оценку значения производной можно улучшить, увеличивая число вспомогательных шагов.

На практике наиболее распространенным методом решения обыкновенных дифференциальных уравнений является метод Рунге-Кутта четвертого порядка. Для оценки значения производной в этом методе используется четыре вспомогательных шага. Это сравнительно простой, достаточно точный (точность ~ h⁴) и быстродействующий метод, алгоритм которого практически всегда приводит к заданной цели. Он, отличается хорошим соотношением точности расчета и объема вычислительной процедуры. В методе Рунге-Кутта угловой коэффициент наклона касательной в начале каждого шага корректируется по результатам расчета касательной в конце шага и в промежуточных точках. Рассмотрим идею метода и ее геометрическую интерпретацию:

1. Через исходную точку с координатами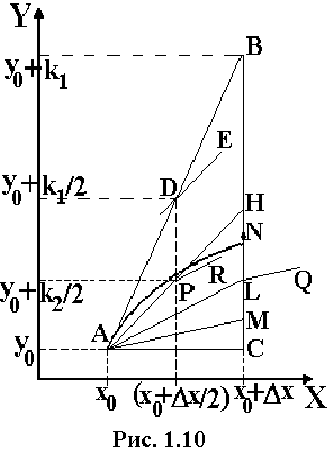 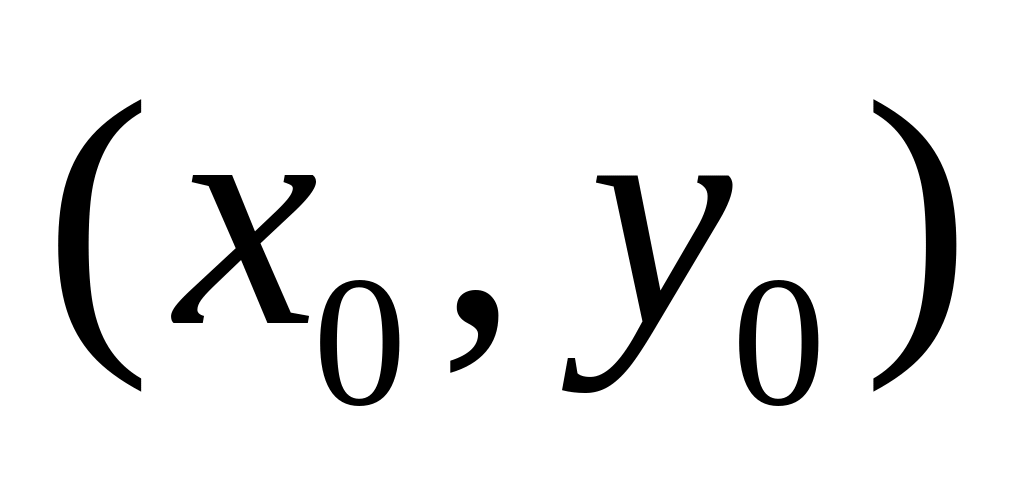, проходит кривая y(x) ординату которой следует определить в конце шага, т.е. для значения аргумента x₀+x. Найдем величину F(x₀,y₀), которая определит тангенс угла наклона касательной к графику в исходной точке, а значит позволит построить касательную AB и рассчитать приращение (так же как и в методе Эйлера) .

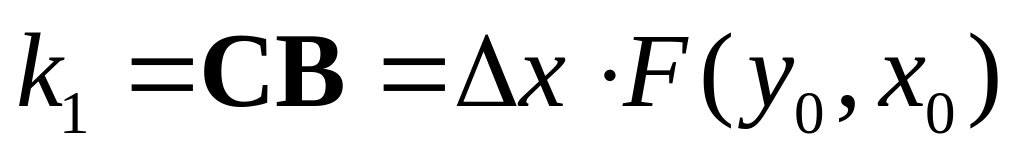2. Движение по касательной АВ осуществляется до точки 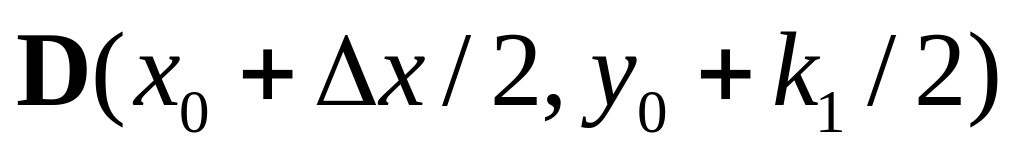. В этой точке рассчитывается функция F(x,y) и определяется новое направление касательной DE к ее графику. Проведем из точки А прямую АН параллельную касательной DE и рассчитаем длину отрезка СН: .

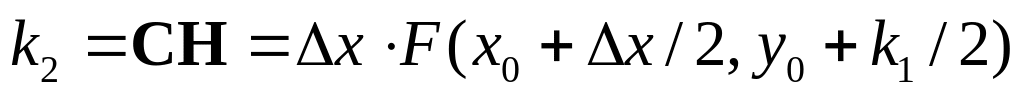3. Определим точку 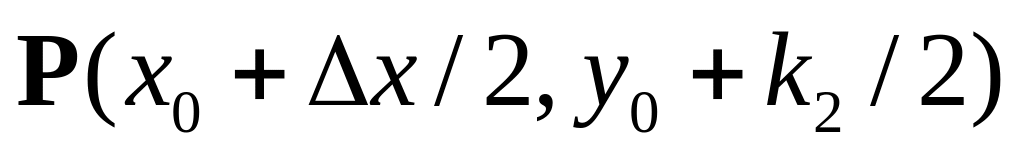и, рассчитав значение функции F(x,y) в этой точке, найдем положение касательной PR к графику. Проведем из точки А прямую АL параллельную касательной PR и рассчитаем длину отрезка СL: .

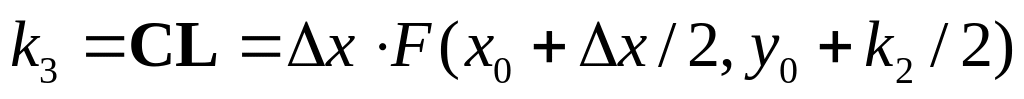4. Рассчитав значение функции F(x,y) в точке L, определим направление касательной LQ и из начальной точки А проведем прямую АМ параллельную этой касательной. Длина отрезка СМ определится формулой: .

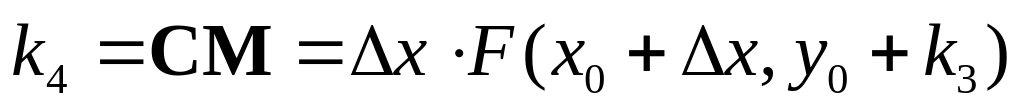5. Определяем положение точки N, близкой к ординате истинной кривой путем нахождения среднего значения длин отрезков CB, CH, CL и CM. При этом слагаемые в сумме следует выбирать с различным весом – с удвоенным вкладом берутся отрезки, которые отсекаются линиями параллельными касательным к точкам в центре шага:

(10.4)

Реализация методов Эйлера и Рунге – Кутта четвертого порядка в среде MathCAD в матричной форме и методом составления программ-функций представлена в приложении. Из сравнения результатов с известным аналитическим решением легко видеть, что точность метода Рунге-Кутта существенно выше.

Отметим, что векторная (или программная) реализация итерационных процедур численных методов позволяет легко продолжить их применение на случай решения систем линейных дифференциальных уравнений.