Задание к лабораторной работе

1. Выбрать свой вариант из таблицы 12, при этом номер задания соответствует последней цифре номера зачетной книжки, l соответствует предпоследней цифре номера зачетной книжки.

2. Дискретизировать функцию, т.е. представить ее в виде вектора, содержащего (2^m-1) компонент. При этом так выбрать форму представления аргумента (изменяя знаменатель в выражении 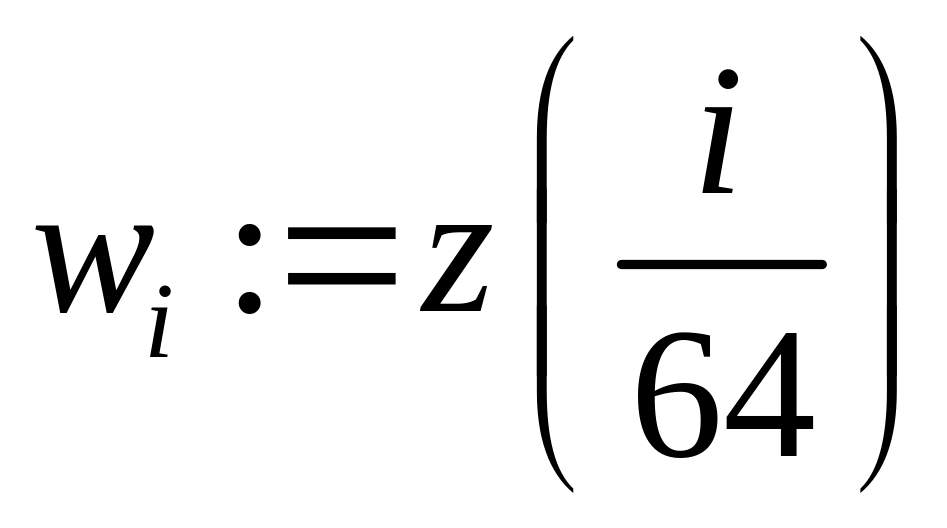), чтобы диапазон изменения его соответствовал бы 2 – 3 периодам колебаний функции.

3. Ввести случайный шум в исходную функцию в соответствии с заданием.

4. Произвести прямое БПФ и перевести сигнал в форму частотного спектра.

5. Произвести цифровую фильтрацию, при этом уровень отсечки ВЧ гармоник определить самостоятельно.

6. Представить графики – исходного сигнала, сигнала с наложенной шумовой компонентой и отфильтрованного сигнала.

7. Представить графики частотного спектра сигналов – зашумленного и отфильтрованного.

Таблица 12.

№ п/п	m	Форма сигнала	Шумовая компонента
0	7
1	8
2	9
3	7
4	8
5	9
6	7
7	8
8	9
9	7

Вопросы для самоконтроля

1. В чем заключается прямое и обратное преобразования Фурье? Каковы особенности быстрого преобразования Фурье (БПФ)?

2. В каком виде должна быть задана функция для того, чтобы можно было произвести БПФ? обратное БПФ?

3. Как построить график спектра сложного сигнала?

4. Как отфильтровать случайную шумовую помеху из полезного сигнала с помощью БПФ? Чем определяется уровень фильтрации?

Лабораторная работа № 9 Решение дифференциальных уравнений методом символьного интегрирования Цель работы

Научиться составлять математическую модель явлений, описываемых простейшими дифференциальными уравнениями и решать их в аналитической форме, используя возможности символьных преобразований пакета MathCAD.

Методические указания

Целый ряд процессов, протекающих в природе и в технических системах, описывается простейшими дифференциальными уравнениями первого порядка с разделяющимися переменными. Среда MathCAD позволяет получить решение их в аналитической форме.

Для описания процесса необходимо составить дифференциальное уравнение, опираясь на известную физическую закономерность, разделить переменные и проинтегрировать обе части уравнения поочередно; полученное выражение разрешить относительно неизвестной функции, получив выражение для нее в общем виде; учесть начальное условие и другие данные задачи для нахождения неизвестных констант.

Рассмотрим пример. Температура тела, вынутого из печи, в течение 5 мин падает от Т₁=100⁰С до Т₂=60⁰С, температура воздуха – Т₀=25⁰С. Найти закон изменения температуры тела и определить температуру тела на протяжении последующих 5 мин через каждые 30 сек. Указание: В основу модели положить закон теплообмена Ньютона – скорость охлаждения dT/dt пропорциональна разности температур тела и окружающей среды (T-T₀). Решение представлено в следующим MathCAD документом.