Задание на лабораторную работу

1. Составить программу решения квадратного уравнения, предусмотреть что программа должна возвращать значения вектора, компонентами которого являются два вещественных корня.

2. Методом половинного деления выполнить решение нелинейного уравнения f(x)=0 из индивидуального задания к лабораторной работе №4 с точностью .

3. Составить программу решения и решить то же самое уравнение методом простой итерации и методом касательных Ньютона. Для организации итерационного цикла использовать процедуру while.

4. Дополнительно: предусмотреть в программе вычисление числа итераций. Ответ организовать в виде вектора.

Вопросы для самоконтроля

1. Каковы инструменты программирования (структурные управляющие конструкции) пакета MathCAD?

2. Какие виды циклов предусмотрены в пакете MathCAD? Для реализации каких задач они используются?

3. В чем заключается модульное программирование? Как реализовать рекурсию в программе?

4. Как запрограммировать прерывание программы с выводом сообщения о диагностической ошибке?

Лабораторная работа № 8

Спектральный анализ и синтез на основе преобразования Фурье

Цель работы

Научиться использовать процедуры быстрого прямого и обратного преобразования Фурье для анализа сложных гармонических сигналов и их фильтрации.

Методические указания

Возможность представления периодических (а при определенных условиях и непериодических) функций совокупностью их гармонических составляющих в виде ряда Фурье эффективно используется во множестве прикладных областей (например, при передаче информации по каналам связи, фильтрации сигналов и др.)

С помощью ряда Фурье периодический сигнал y(t) на отрезке [0,T] может быть представлен в виде:

,

где f₁ =1/T– частота первой гармоники периодического сигнала, а коэффициенты ряда a_k и b_k определяют вклад косинусной и синусной составляющих k-ой гармоники и вычисляются по формулам:

Часто используется иная формула ряда Фурье, упрощающая его синтез:

,

где амплитуда A_k и фаза _k k-ой гармоники выражаются через коэффициенты ряда a_k и b_k.

Переход от функции y(t) к параметрам ее ряда Фурье (амплитудам и фазам гармоник) называется прямым преобразованием Фурье. Соответственно, обратный переход называется обратным преобразованием Фурье. Непосредственная компьютерная реализация этих переходов вызывает затруднения, поскольку необходимо вычислять с заданной точностью интегралы от быстро осциллирующих подынтегральных функций. Поэтому были разработаны методы быстрого (дискретного) преобразования Фурье (FFT – Fast Fourier Transform).

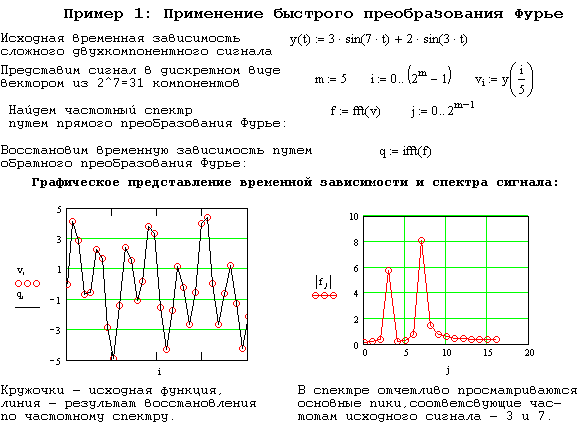
Функция fft(v) пакета MathCAD выполняет быстрое преобразование Фурье (БПФ) для вектора, содержащего 2^m компонент (где m – целое число) и формирует вектор, состоящий из (2^m+1) комплексных чисел, модуль и аргумент которых соответствуют амплитудам и фазам гармоник ряда Фурье.

Таким образом эта процедура переводит временную зависимость в частотную область – находит спектр сигнала. Функция ifft(v) быстрого обратного Фурье вновь переводит частотный спектр во временную зависимость. Построение быстрого преобразования Фурье рассмотрено в примере 1.

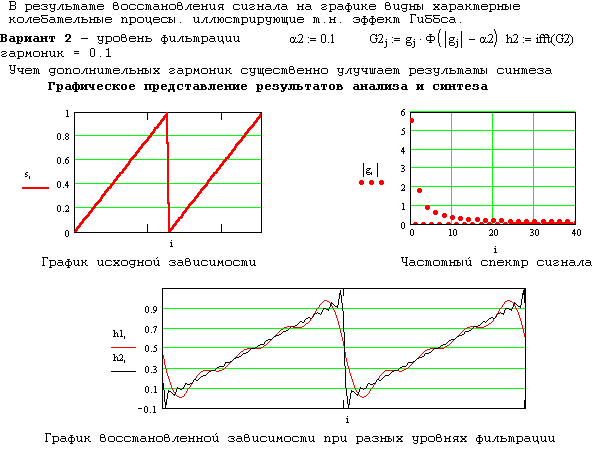
БПФ широко применяется при решении задач аппроксимации функций. Так, при ограниченном числе гармоник приближение функции тригонометрическим рядом Фурье обеспечивает наименьшую среднеквадратичную погрешность. Применение БПФ для спектрального анализа сигналов с учетом ограничения числа гармоник (отсечение части спектра) рассмотрено в примере 2.

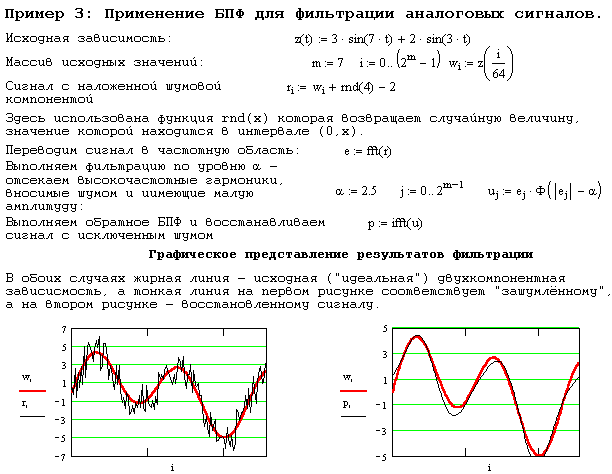
Аналогичная методика цифровой фильтрации применяется в случае необходимости исключения из полезного сигнала высокочастотного шума вносимого случайными помехами. Идея фильтрации заключается в том, что компоненты вектора, соответствующие внесенному шуму, имеют небольшую амплитуду (модуль) и, потому, могут быть отброшены. Пример фильтрации зашумленного сигнала путем отсечки высокочастотных гармоник приведен в приведен в примере 3. Качество фильтрации здесь, как и в предыдущем случае определяется уровнем фильтрации .