Лабораторная работа № 6 Аппроксимация функций. Построение регрессионных зависимостей методом наименьших квадратов. Цель работы

Ознакомиться с основными приемами проведения аппроксимации линейными и нелинейными функциями. Научиться определять коэффициенты регрессионных зависимостей.

Методические указания

Наиболее распространенным методом аппроксимации экспериментальных данных является метод наименьших квадратов. Он позволяет использовать аппроксимирующие функции произвольного вида и относится к группе глобальных методов. Критерием близости в методе наименьших квадратов является требование минимальности суммы квадратов отклонений от аппроксимирующей функции до экспериментальных точек:

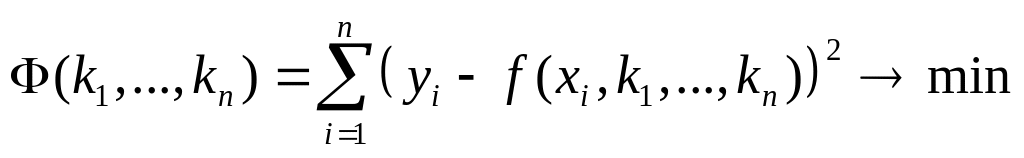, 6.1

где параметры k_i варьируются для того, чтобы достичь минимума функции.

Таким образом, не требуется, чтобы аппроксимирующая функция проходила через все заданные точки, что особенно важно при аппроксимации данных, заведомо содержащих погрешности. Важной особенностью метода является то, что аппроксимирующая функция может быть произвольной. Ее вид определяется особенностями решаемой задачи, например, физическими соображениями, если проводится аппроксимация результатов физического эксперимента⁵.

Наиболее часто встречаются аппроксимация прямой линией (линейная регрессия – простейший вариант метода наименьших квадратов), аппроксимация полиномом (полиномиальная регрессия), аппроксимация линейной комбинацией произвольных функций. Кроме того, часто бывает возможно путем замены переменных свести задачу к линейной (провести линеаризацию). Например, пусть аппроксимирующая функция ищется в виде: . Прологарифмируем это выражение и введем обозначения , . Тогда в новых обозначениях задача сводится к отысканию коэффициентов линейной функции: .

Применение метода наименьших квадратов для аппроксимации экспериментальных данных (вектор абсцисс узловых точек – X, вектор ординат узловых точек – Y) прямой линией можно проделать следующим образом:

• с помощью функций slope(X,Y) (в переводе: наклон), которая определяет угловой коэффициент прямой. и intercept(X,Y) (в переводе: отложить отрезок на линии), которая определяет точку пересечения графика с вертикальной осью;

• с помощью функции line(X,Y) – определяет оба параметра аппроксимирующей прямой в виде вектора;

• путем поиска минимума функции среднеквадратичного отклонения.

Рассмотрим применение упомянутых процедур для определения параметров аппроксимирующей прямой в следующем MathCAD документе:

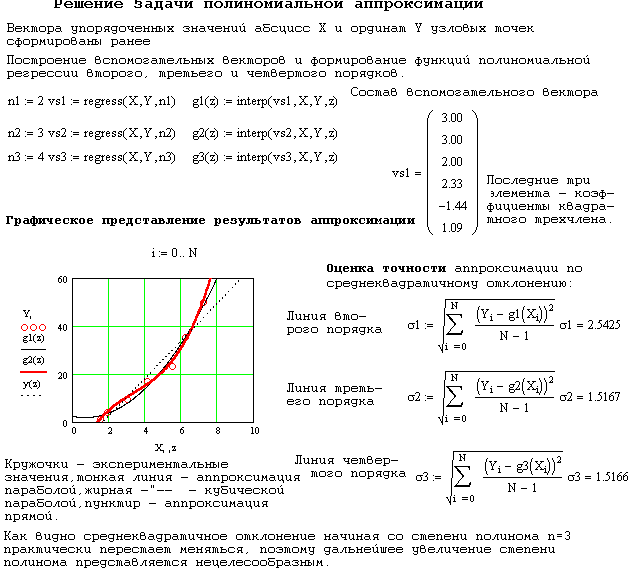
Набор экспериментальных точек может быть аппроксимирован полиномиальной зависимостью. Для этой цели служит вспомогательная встроенная функция regress(X,Y,n), которая формирует вектор vs, тем самым подготавливая данные, необходимые для работы функции interp. Первые три элемента вектора vs используются функцией interp, а остальные – являются коэффициентами аппроксимирующего полинома. Рассмотренная ранее функция interp(vs,X,Y,z) возвращает значение построенной аппроксимирующей функции в т. z. Обычно степень выбираемого для аппроксимации полинома не является высокой (если ее выбрать на единицу меньше, чем число точек, то задача сведется к глобальной интерполяции и построению интерполяционного полинома Лагранжа). Если заранее, из физических соображений, неизвестно какова должна быть степень аппроксимирующего полинома, то для оценки ее можно определить величину среднеквадратичного отклонения и выбрать ту, которая соответствует наименьшему ее значению. Построение полиномиальной регрессии для сформированного ранее набора упорядоченных экспериментальных данных проиллюстрировано в следующем MathCAD документе:

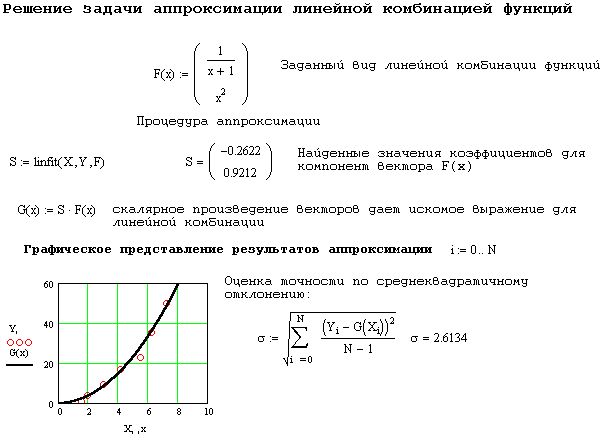
Для аппроксимации данных по методу наименьших квадратов линейной комбинацией произвольных функций в пакете MathCAD предоставляется пользователям встроенная функция linfit .Функция linfit имеет три аргумента: вектор X – абсциссы заданных точек, вектор Y – ординаты заданных точек и функция F – содержит набор функций, который будет использоваться для построения линейной комбинации.

В качестве примера будем искать аппроксимирующую функцию в виде линейной комбинации функций: , т. е. представим ее в виде:

.

Задачей построения регрессионной (аппроксимирующей) зависимости является нахождение неизвестных коэффициентов a и b. Пример проведения аппроксимации в виде линейной комбинации функций приведен в следующем MathCAD документе:

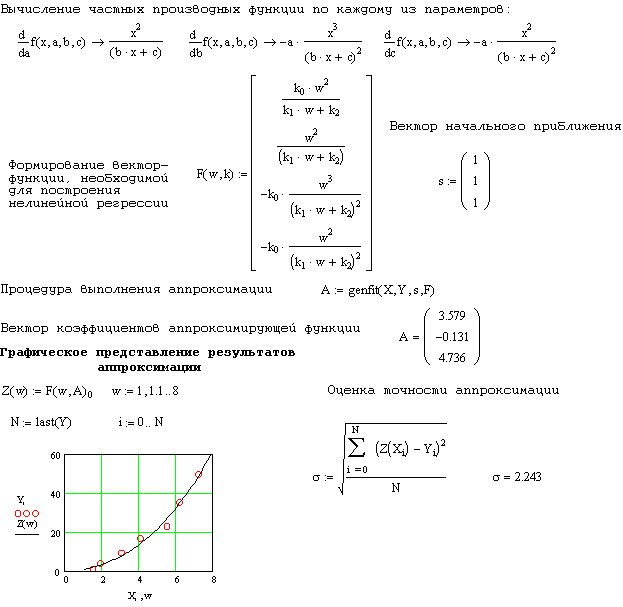
Для построения регрессионной зависимости (нахождения аппроксимирующей функции) общего вида используется функция genfit(X,Y,s,F). Она имеет следующие параметры: X, Y – векторы, содержащие координаты заданных точек, F – функция, задающая искомую функциональную n–параметрическую зависимость и частные производные этой зависимости по этим параметрам, s – вектор, задающий начальные приближения для поиска параметров

Проведем, в качестве примера, аппроксимацию функцией вида . При этом, хотя выражения для производных можно вычислить «врукопашную» будем использовать возможности символьного блока пакета MathCAD. Пример построения регрессии общего вида дан в следующем документе: