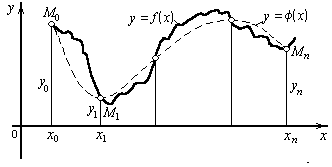- •Темы и объем лабораторных занятий (академические часы)
- •Введение
- •Лабораторная работа №1 Основы работы с MathCad Цель работы
- •Методические указания
- •Операторы
- •Типы данных
- •Функции
- •Текстовые фрагменты
- •Графические области
- •2. Traces (след) – управляет параметрами линий, которыми строится график
- •3. Labels (метки) – установка надписей по осям и титульной надписи
- •4. Defaults (умолчание) – задание режима по умолчанию
- •Порядок выполнения лабораторной работы
- •Вопросы для самоконтроля
- •Лабораторная работа № 2 Работа с векторами и матрицами в системе mathcad Цель работы
- •Методические указания
- •Задание на лабораторную работу
- •Вопросы для самоконтроля
- •Лабораторная работа №3 Решение систем уравнений Цель работы
- •Методические указания
- •Задание на лабораторную работу
- •Вопросы для самоконтроля
- •Лабораторная работа №4 Решение нелинейных уравнений Цель работы
- •Методические указания
- •Метод половинного деления
- •Метод хорд
- •Метод Ньютона
- •Метод простой итерации (последовательных итераций)
- •Задание на лабораторную работу
- •Вопросы для самоконтроля
- •Лабораторная работа №5 Интерполяция функций Цель работы
- •Методические указания
- •Задание к лабораторной работе
- •Вопросы для самоконтроля
- •Лабораторная работа № 6 Аппроксимация функций. Построение регрессионных зависимостей методом наименьших квадратов. Цель работы
- •Методические указания
- •Задание к лабораторной работе
- •Вопросы для самоконтроля
- •Лабораторная работа №7 Основы программирования в пакете MathCad Цель работы
- •Методические указания
- •Задание на лабораторную работу
- •Задание к лабораторной работе
- •Вопросы для самоконтроля
- •Лабораторная работа № 9 Решение дифференциальных уравнений методом символьного интегрирования Цель работы
- •Методические указания
- •Задание на лабораторную работу
- •Вопросы для самоконтроля
- •Задание к лабораторной работе
- •Вопросы для самоконтроля
- •Задание на лабораторную работу
- •1. Цель курсовой работы
- •2. Введение
- •3. Аналитические методы
- •3.1 Классический метод
- •3.2. Метод операционного исчисления
- •4. Численный метод решения дифференциальных уравнений
- •5. Задание на курсовую работу
- •5.1. Выбор варианта
- •5.2. Порядок действий
- •Требования к пояснительной записке:
- •Приложение: Примеры выполнения этапов курсовой работы
- •Рекомендуемая литература.
- •65029. Одесса-29, Дидрихсона, 8.
Лабораторная работа №5 Интерполяция функций Цель работы
Приобретение навыков решения на ЭВМ задачи локальной интерполяции функции и вычисления ее приближенного значения в промежутках между узловыми точками.
Методические указания
Аппроксимация функций заключается в приближенной замене заданной функции f(x) некоторой функцией (x) так, чтобы отклонение функции (x) от f(x) в заданной области было наименьшим2. Функция (х) при этом называется аппроксимирующей.
Аппроксимацию называется точечной (дискретной) или непрерывной (интегральной) в зависимости от того, как строится приближение – на дискретном наборе точек или на непрерывном их множестве (отрезке). Примером второго случая является разложение функции в степенной ряд Тейлора.
Одним из видов аппроксимации функций является задача интерполяции. Необходимость ее связана с тем, что для вычисления значений функции, ее производных в произвольных точках и величин интегралов необходимо аналитическое описание изучаемой функции, а оно либо достаточно сложно (случаи спецфункций – гамма-функция, эллиптическая функция и др.) либо вообще отсутствует (функция задана таблично).
Пусть
на отрезке
[a,b]
задан
дискретный набор точек
![]() ,
называемых узлами
интерполяции,
причем среди этих точек нет совпадающих,
а также значения некоторой функции f(x)
в этих точках:
,
называемых узлами
интерполяции,
причем среди этих точек нет совпадающих,
а также значения некоторой функции f(x)
в этих точках:
f(x0) = y0, f(x1) = y1, . . ., f(xn) = yn.
Требуется построить функцию (х) (интерполяционная функция), принадлежащую определенному классу (например, полиномов, дробно-рациональных или гармонических функций) и принимающую в узлах интерполяции те же значения, что и f(x), т.е. такую, что:
(x0) = y0, (x1) = y1, . . ., (xn) = yn. (5.1)
Геометрически это означает, что нужно найти кривую y = (х) определенного типа, проходящую через заданную систему точек M(xi, yi) (i = 0, 1, ..., n) (рис. 9). В такой общей постановке задача может иметь бесконечное множество решений или совсем не иметь их. Задача становится однозначной, если вместо произвольной функции (х) искать полином (х) степени не выше n – интерполяционный полином, удовлетворяющий условиям (5.1).
Рис. 9. К пояснению понятия аппроксимации |
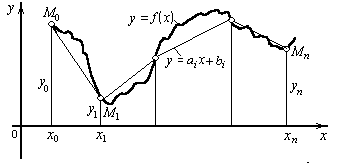
Рис. 10. Линейная интерполяция |
Найдя
интерполяционный полином, мы можем
вычислить значения функции
![]() между узлами (провести
интерполяцию
в узком смысле слова),
а также определить значение функции
даже за пределами заданного интервала
(провести экстраполяцию3).
Если полином един для всей области
интерполяции, то говорят о глобальной
интерполяции,
а если между различными узлами полиномы
различны, то говорят о кусочной
или локальной
интерполяции.
между узлами (провести
интерполяцию
в узком смысле слова),
а также определить значение функции
даже за пределами заданного интервала
(провести экстраполяцию3).
Если полином един для всей области
интерполяции, то говорят о глобальной
интерполяции,
а если между различными узлами полиномы
различны, то говорят о кусочной
или локальной
интерполяции.
Задача глобальной интерполяции обычно решается с помощью интерполяционной формулы Лагранжа:
![]() .
(5.2)
.
(5.2)
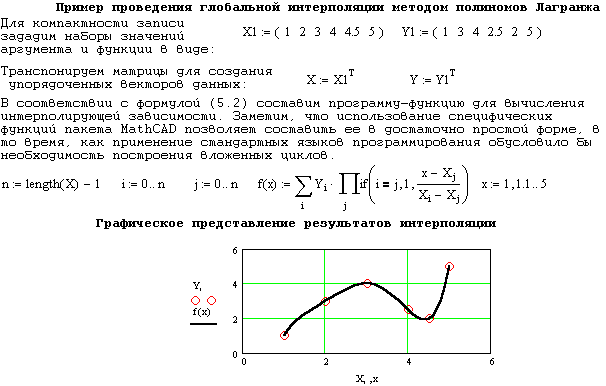
При нарастании числа точек (выше 6-8) полином Лагранжа становится достаточно громоздким и практически непригодным. Это связано с тем, что степень его лишь на единицу меньше числа дискретного набора точек (экспериментальных значений функции). Поэтому при значительном числе точек чаще решают задачу локальной интерполяции.
Простейшим видом локальной интерполяции является линейная интерполяция, заключающаяся в том, что заданные точки М(xi, yi) (i = 0, 1, ..., n) соединяются прямолинейными отрезками, и функция f(x) приближается ломаной с вершинами в данных точках (рис. 10). Задача линейной интерполяции в пакете MathCAD решается с помощью встроенной функции linterp(vx,vy,z), которая использует векторы данных vx и vy, чтобы возвратить интерполируемое значение, соответствующее третьему аргументу z. Аргументы vx и vy должны быть векторами одинаковой длины, и вектор vx должен содержать вещественные значения, расположенные по возрастания (если это не так, то их необходимо вначале упорядочить). Функция соединяет узловые точки отрезками прямых, создавая таким образом ломаную. Интерполируемое значение для конкретного z есть ордината у соответствующей точки ломаной.
Если величина x, расположена перед первой (или за последней) точкой в векторе vx, то MathCAD продолжает ломаную прямой линией, проходящей через первые две (последние две) точки данных. Пример проведения линейной интерполяции:
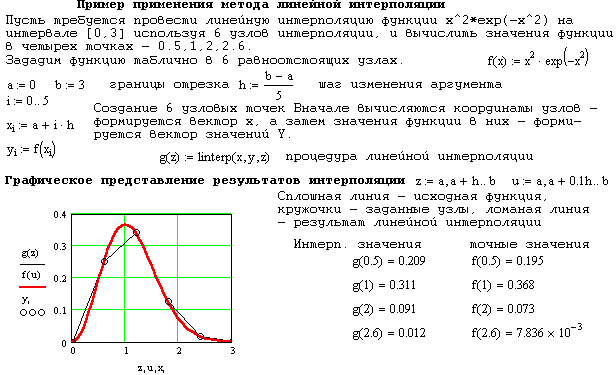
Усложнением метода линейной является квадратичная интерполяция – в качестве интерполяционной функции принимается квадратный трехчлен, причем интерполяция проводится по трем ближайшим точкам.
В настоящее время среди методов локальной интерполяции наибольшее распространение получила интерполяция кубическими сплайнами (от английского слова spline – гибкая линейка). Основные идеи теории сплайнов сформировались как результат математического описания поведения гибких реек из упругого материала (механические сплайны), которыми издавна пользовались чертежники при необходимости проведения через заданные точки достаточно
Рис. 11. Положение минимума энергии упругой рейки
|
Кубическая сплайн-интерполяция позволяет провести кривую, которая образуется путем создания и последующей «состыковки» ряда кубических полиномов, проходящих через наборы из трех смежных точек.
На
каждом интервале
![]() кубический интерполирующий сплайн S(x)
(полином третьей степени):
кубический интерполирующий сплайн S(x)
(полином третьей степени):
![]() ,
,
удовлетворяет
условиям (5.1). Если
всего задано n
узлов, то число интервалов – (![]() ).
Значит, требуется определить
).
Значит, требуется определить
![]() неизвестных коэффициентов кубических
полиномов. Условие (5.1) дает нам n
уравнений. Условие непрерывности функции
и ее первой и второй производных во
внутренних
узлах интервала дает дополнительно
неизвестных коэффициентов кубических
полиномов. Условие (5.1) дает нам n
уравнений. Условие непрерывности функции
и ее первой и второй производных во
внутренних
узлах интервала дает дополнительно
![]() уравнений
уравнений
![]()
Всего
имеем
![]() различных уравнений. Два недостающих
уравнения можно получить, задавая
условия на краях интервала: при этом
можно считать, что кривая сплайна
приближается в граничных точках к прямой
линии, или к параболе или же к кубической
кривой. В пакете MathCAD
имеется три сплайн-функции: lspline
(vx,vy),
pspline(vx,vy),
cspline(vx,vy)
каждая из
которых соответствует заданию линейных,
квадратичных (параболических) или
кубических условий на границах интервала.
Аргументы vx
и vy
удовлетворяют тем же требованиям, что
и в случае линейной интерполяции.
Сплайн-функции возвращают вектор
коэффициентов вторых производных,
обозначаемый vs.
Этот вектор используется в функции
interp(vs,vx,vy,z),
которая возвращает интерполируемое
значение, соответствующее аргументу
z.
различных уравнений. Два недостающих
уравнения можно получить, задавая
условия на краях интервала: при этом
можно считать, что кривая сплайна
приближается в граничных точках к прямой
линии, или к параболе или же к кубической
кривой. В пакете MathCAD
имеется три сплайн-функции: lspline
(vx,vy),
pspline(vx,vy),
cspline(vx,vy)
каждая из
которых соответствует заданию линейных,
квадратичных (параболических) или
кубических условий на границах интервала.
Аргументы vx
и vy
удовлетворяют тем же требованиям, что
и в случае линейной интерполяции.
Сплайн-функции возвращают вектор
коэффициентов вторых производных,
обозначаемый vs.
Этот вектор используется в функции
interp(vs,vx,vy,z),
которая возвращает интерполируемое
значение, соответствующее аргументу
z.
Для
получения наилучших результатов z
должно
находится между самыми большими и самыми
маленькими значениями vx
- маловероятно, что будут полезны
значения, вычисленные
![]() вне
этого диапазона. Сплайны предназначены
для интерполяции, а не для экстраполяции.
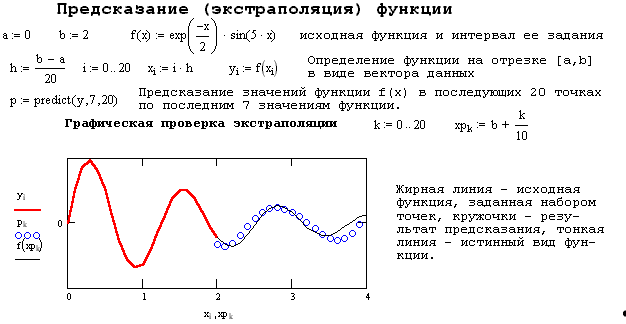
Задача экстраполяции
вперед4
(линейного
предсказания) решается в пакете MathCAD
с помощью функции predict(v,m,n),
которая использует линейный алгоритм
предсказания. Она полезна, когда
экстраполируемая функция является
гладкой и монотонной или осциллирующей,
хотя не обязательно периодической.
Функция возвращает n
предсказанных
значений, основанных на m
последовательных последних значениях
вектора данных v.
Вначале вычисляются коэффициенты
предсказания, а затем используются
последние m
точек чтобы
предсказать координаты (m+1)
- ой точки,
т.е. фактически создается скользящее
окно шириной в m
точек.
вне
этого диапазона. Сплайны предназначены
для интерполяции, а не для экстраполяции.
Задача экстраполяции
вперед4
(линейного
предсказания) решается в пакете MathCAD
с помощью функции predict(v,m,n),
которая использует линейный алгоритм
предсказания. Она полезна, когда
экстраполируемая функция является
гладкой и монотонной или осциллирующей,
хотя не обязательно периодической.
Функция возвращает n
предсказанных
значений, основанных на m
последовательных последних значениях
вектора данных v.
Вначале вычисляются коэффициенты
предсказания, а затем используются
последние m
точек чтобы
предсказать координаты (m+1)
- ой точки,
т.е. фактически создается скользящее
окно шириной в m
точек.
Пример построения в пакете MathCAD кубических сплайнов через узловые точки приведены в следующем документе:
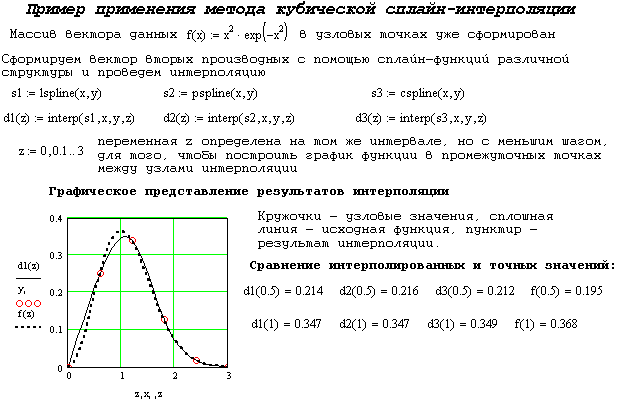
Пример использования функции predict дан в следующем документе: