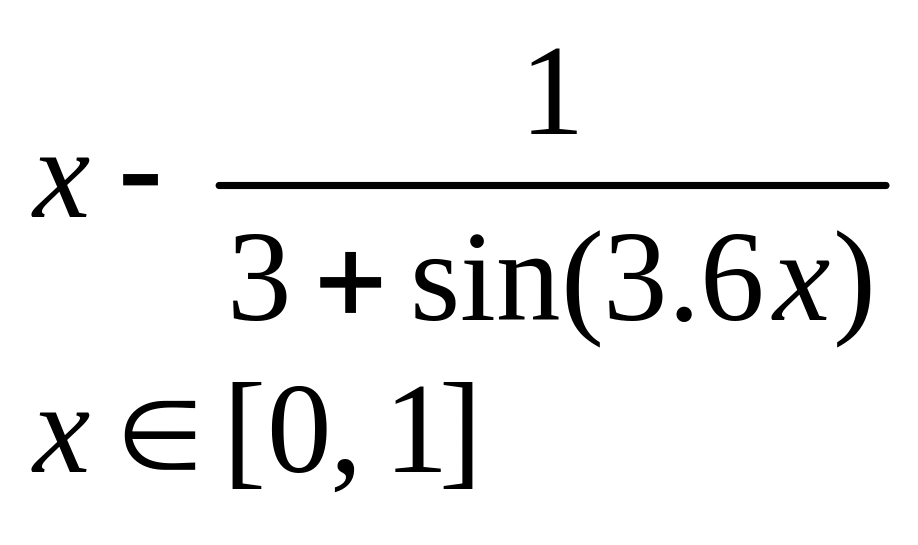- •Темы и объем лабораторных занятий (академические часы)
- •Введение
- •Лабораторная работа №1 Основы работы с MathCad Цель работы
- •Методические указания
- •Операторы
- •Типы данных
- •Функции
- •Текстовые фрагменты
- •Графические области
- •2. Traces (след) – управляет параметрами линий, которыми строится график
- •3. Labels (метки) – установка надписей по осям и титульной надписи
- •4. Defaults (умолчание) – задание режима по умолчанию
- •Порядок выполнения лабораторной работы
- •Вопросы для самоконтроля
- •Лабораторная работа № 2 Работа с векторами и матрицами в системе mathcad Цель работы
- •Методические указания
- •Задание на лабораторную работу
- •Вопросы для самоконтроля
- •Лабораторная работа №3 Решение систем уравнений Цель работы
- •Методические указания
- •Задание на лабораторную работу
- •Вопросы для самоконтроля
- •Лабораторная работа №4 Решение нелинейных уравнений Цель работы
- •Методические указания
- •Метод половинного деления
- •Метод хорд
- •Метод Ньютона
- •Метод простой итерации (последовательных итераций)
- •Задание на лабораторную работу
- •Вопросы для самоконтроля
- •Лабораторная работа №5 Интерполяция функций Цель работы
- •Методические указания
- •Задание к лабораторной работе
- •Вопросы для самоконтроля
- •Лабораторная работа № 6 Аппроксимация функций. Построение регрессионных зависимостей методом наименьших квадратов. Цель работы
- •Методические указания
- •Задание к лабораторной работе
- •Вопросы для самоконтроля
- •Лабораторная работа №7 Основы программирования в пакете MathCad Цель работы
- •Методические указания
- •Задание на лабораторную работу
- •Задание к лабораторной работе
- •Вопросы для самоконтроля
- •Лабораторная работа № 9 Решение дифференциальных уравнений методом символьного интегрирования Цель работы
- •Методические указания
- •Задание на лабораторную работу
- •Вопросы для самоконтроля
- •Задание к лабораторной работе
- •Вопросы для самоконтроля
- •Задание на лабораторную работу
- •1. Цель курсовой работы
- •2. Введение
- •3. Аналитические методы
- •3.1 Классический метод
- •3.2. Метод операционного исчисления
- •4. Численный метод решения дифференциальных уравнений
- •5. Задание на курсовую работу
- •5.1. Выбор варианта
- •5.2. Порядок действий
- •Требования к пояснительной записке:
- •Приложение: Примеры выполнения этапов курсовой работы
- •Рекомендуемая литература.
- •65029. Одесса-29, Дидрихсона, 8.
Задание на лабораторную работу
Номер задания выбирается по таблице в соответствии с последней цифрой номера зачетной книжки, а способ выполнения определяется суммой двух последних цифр номера зачетной книжки, которая обозначена через Z.
Построить график функции f(x) (табл. 8) и, учитывая, что интервал локализации корня выделен, приблизительно определить один из корней уравнения. Решить нелинейное трансцендентное уравнение f(x)= 0 с точностью = 10–4. Если Z – четное, то решение следует провести методом простой итерации, методом хорд и проверить, используя встроенную функцию MathCAD – root. Если Z – нечетное, то необходимо решить уравнение методом Ньютона (касательных), методом хорд и проверить, используя блок решения c функцией Minerr. В каждом случае определить число итераций с помощью функции last.
Таблица 8.
№ варианта |
f(x) |
№ варианта |
f(x) |
0 |
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
В соответствие с заданным полиномом g(x) (табл. 9) решить нелинейное алгебраическое уравнение g(x)=0 следующими способами:
Если Z – четное, то использовать функции polyroots, solve, выводя на экран 4 знака решения.
Если же Z – нечетное, то решить уравнение, используя следующие команды Символы (Symbolics) Переменные (Variables) Вычислить (Solve) и блок решения с функцией Find.
Таблица 9.
№ варианта |
g(x) |
№ варианта |
g(x) |
0 |
x4 – 2x3 + x2 - 12x + 20 |
1 |
x4 + x3 - 17x2 - 45x - 100 |
2 |
x4 + 6x3 + x2 - 4x - 60 |
3 |
x4 - 5x3 + x2 - 15x + 50 |
4 |
x4 - 14x2 - 40x - 75 |
5 |
x4 - 4x3 - 2x2 - 20x + 25 |
6 |
x4 - x3 + x2 - 11x + 10 |
7 |
x4 + 5x3 + 7x2 + 7x - 20 |
8 |
x4 - x3 - 29x2 - 71x -140 |
9 |
x4 - 7x3 + 7x2 - 5x + 100 |
Вопросы для самоконтроля
В чем заключаются итерационные методы решения нелинейных уравнений? Какова последовательность действий при решении уравнений итерационными способами?
Опишите алгоритм основных итерационных методов решения нелинейных уравнений и реализацию его в пакете MathCAD с помощью функции while.
Какие функции для решения одного уравнения в MathCAD вы знаете? В чем их отличие?
Какие аргументы функции root не обязательны?
В каких случаях MathCAD не может найти корень уравнения?
Как изменить точность, с которой функция root ищет корень?
Когда для решения уравнений можно использовать функцию polyroot?
В каких случаях MathCAD не может найти решение системы уравнений?
Как использовать блок решения для нахождения численного и символьного решения нелинейного уравнения?