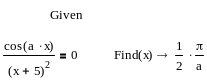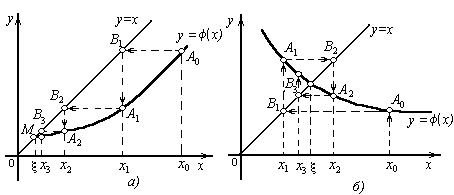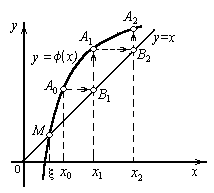Метод простой итерации (последовательных итераций)

Заменим исходное нелинейное уравнение f(х)=0 равносильным уравнением вида x=(x). Если известно начальное приближение корня х = х₀, то новое приближение может быть получено по формуле: х₁=(х₀). Далее, подставляя каждый раз новое значение корня в исходное уравнение получаем последовательность значений:

Геометрическая интерпретация метода состоит в том, что каждый действительный корень уравнения является абсциссой точки пересечения М кривой у=(х) с прямой у=х (рис. 8). Отправляясь от произвольной т. А₀ [x₀, (x₀)] начального приближения, строим ломаную А₀В₁А₁В₂А₂.., которая имеет форму «лестницы» (рис. 8, а) если производная ’(x) положительна и форму «спирали» (рис. 8, б) в противоположном случае.

	в)
Рис. 8. Метод простой итерации: а, б – сходящаяся итерация, в – расходящаяся итерация.

Отметим, что следует заранее проверить пологость кривой (х), поскольку если она не является достаточно пологой ( >1), то процесс итерации может быть расходящимся (рис. 8, в).

Пример 4. Решить уравнение x³ – x – 1 = 0 методом простой итерации с точностью  = 10^-3. Реализация этой задачи представлена следующим MathCAD документом.

Реализация приближенных методов решения встроенными функциями MathCAD

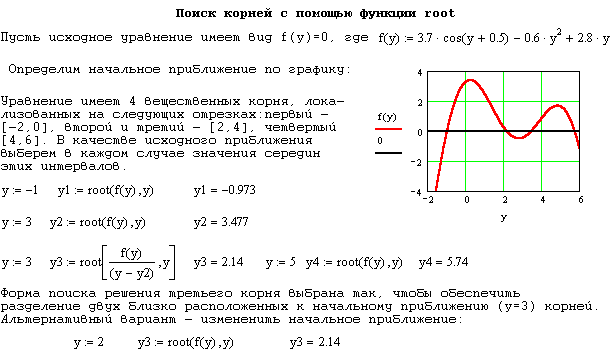
Использование функции root

Для уравнений вида f(x) = 0 решение находится с помощью функции: root(f(х),х,a,b), которая возвращает значение х, принадлежащее отрезку [a, b], при котором выражение или функция f(х) обращается в 0. Оба аргумента этой функции x и f(x) должны быть скалярами, а аргументы a, b – являются необязательными и, если используются, то должны быть вещественными числами, причем a < b. Функция позволяет находить не только вещественные, но и комплексные корни уравнения (при выборе начального приближения в комплексной форме).

Если уравнение не имеет корней, они расположены слишком далеко от начального приближения, начальное приближение было вещественным, а корни – комплексные, функция f(х) имеет разрывы (локальные экстремумы между начальными приближениями корня) то появится сообщение (отсутствует сходимость). Причину ошибки можно выяснить, исследуя график f(x). Он поможет выяснить наличие корней уравнения f(x) = 0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее будет сходиться функция root.

Для выражения f(x) с известным корнем а нахождение дополнительных корней f(x) эквивалентно поиску корней уравнения h(x)=f(x)/(x‑a). Проще искать корень выражения h(x), чем пробовать искать другой корень уравнения f(x)=0, выбирая различные начальные приближения. Подобный прием полезен для нахождения корней, расположенных близко друг к другу, он реализован в приведенном ниже документе.

Пример 5. Решить алгебраическое уравнения с помощью функции root:

Примечание. Если увеличить значение системной переменной TOL (tolerance), то функция root будет сходиться быстрее, но ответ будет менее точен, а при уменьшении TOL более медленная сходимость обеспечивает более высокую точность, соответственно. Последнее необходимо, если требуется различить два близко расположенных корня, или же, если функция f(x) имеет малый наклон около искомого корня, поскольку итерационный процесс в этом случае может сходиться к результату, отстоящему от корня достаточно далеко. В последнем случае альтернативой повышения точности является замена уравнения f(x) = 0 на g(x) = 0, где .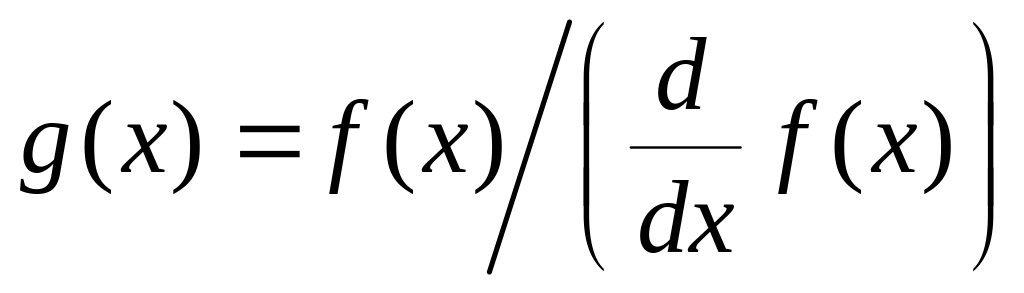

Использование функции polyroots

Если функция f(x) является полиномом степени n , то для решения уравнения f(x)=0 лучше использовать функцию polyroots(a), нежели root, поскольку она не требует начального приближения и возвращает сразу все корни, как вещественные, так и комплексные. Аргументом ее является вектор a, составленный из коэффициентов исходного полинома. Его можно сформировать вручную или с помощью команды Символы  Коэффициенты полинома (переменная полинома x выделяется курсором). Пример применения функции polyroots:

Использование функции solve и блока решений

Блок решений с ключевыми словами (Given – Find или Given – Minerr) или функция solve позволяют найти решение произвольного нелинейного уравнения, если предварительно задано начальное приближение.

Отметим, что между функциями Find и root наблюдается своеобразная конкуренция. С одной стороны, Find позволяет искать корни, как уравнений, так и систем. С этих позиций функция root как бы и не нужна. Но с другой стороны, конструкцию Given-Find невозможно вставить в MathCAD программы. Поэтому в программах приходится подстановками сводить систему к одному уравнению и использовать функцию root.

Символьное решение уравнений в пакете MathCAD

Во многих случаях, MathCAD позволяет найти аналитическое решение уравнения. Для того чтобы найти решение уравнения в аналитическом виде необходимо записать выражение и выделить в нем переменную. После этого выбираем из пункта меню Symbolic подпункт Solve for Variable.

_{Другими вариантами нахождения решения в символьной форме являются (приводятся примеры решения того же уравнения) – использование функции solve из палитры математических операций Символы (Symbolic).}

использование блока решения (с ключевыми словами Given - Find)