Метод половинного деления
Отрезок, на концах которого функция принимает значения разного знака, делится пополам и, если корень лежит правее центральной точки, то к центру подтягивается левый край, а если – левее, то правый край. Новый суженный отрезок снова делится пополам и процедура повторяется. Этот метод прост и надежен, всегда сходится (хотя часто медленно – расплата за простоту!). Программная реализация его в пакете MathCAD рассмотрена в лабораторной работе №7 данного пособия.
Метод хорд
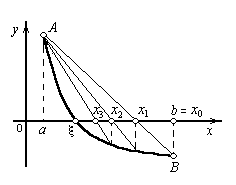
В качестве последовательных приближений к корню уравнения принимаются значения х1, х2, ..., хn точек пересечения хорды АВ с осью абсцисс (рис. 6).
Уравнение
хорды AB имеет
вид:
.
Для точки пересечения ее с осью абсцисс
(х=х1,
y=0) имеем:
.
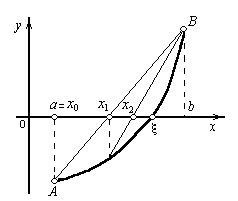
Пусть для определенности кривая у = f(x) будет выпукла вниз и, следовательно, расположена ниже своей хорды АВ, т.е. на отрезке [a,b] f (x)>0. Возможны два случая: f(а)>0 (рис. 6, а) и f(а)<0 (рис. 6, б).
а) |
б) |
Рис. 6. Метод хорд решения нелинейного уравнения |
|
В
первом случае, конец а
неподвижен. Последовательные итерации
образуют ограниченную монотонно
убывающую последовательность:
и
определяются согласно уравнениям:
x0
= b;
.
(4.1)
Во
втором случае неподвижен конец b,
последовательные итерации образуют
ограниченную монотонно возрастающую
последовательность:
и
определяются согласно уравнениям:
x0
= а;
.
(4.2)
Таким образом, неподвижным следует выбирать тот конец, для которого знак функции f(х) и ее второй производной f (х) совпадают, а последовательные приближения xn лежат по ту сторону корня , где эти знаки противоположны. Итерационный процесс продолжается до тех пор, пока модуль разности двух последовательных приближений не станет меньше, чем заданная точность решения.
Пример 2. Найти положительный корень уравнения f(x) x3–0,2x2–0,2х–1,2 = 0 с точностью = 0,01. (Точный корень уравнения = 1,2).
Для организации итерационных вычислений в MathCAD документе используется функция until(a, z), которая возвращает значение величины z, пока выражение a не становится отрицательным.
Метод Ньютона
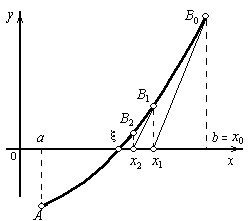
Отличие этого метода от предыдущего состоит в том, что вместо хорды на каждом шаге проводится касательная к кривой y=f(x) при x=хi и ищется точка пересечения ее с осью абсцисс (рис. 7):
Рис. 7. Метод касательных Ньютона |
При этом не обязательно задавать отрезок [а, b], содержащий корень уравнения), а достаточно лишь задать начальное приближение корня x=х0, которое должно находиться на том же конце интервала [а, b], где знаки функции и ее второй производной совпадают.
Уравнение
касательной, проведенной к кривой y
= f(x)
через точку В0
с координатами
х0
и f(х0),
имеет вид:
Отсюда
найдем следующее приближение корня х1
как абсциссу
точки пересечения касательной с осью
Ох (y
= 0):
Аналогично могут быть найдены и последующие приближения как точки пересечения с осью абсцисс касательных, проведенных в точках В1, В2 и так далее. Формула для (i +1) приближения имеет вид:
Условием
окончания итерационного процесса
является неравенство f(xi)<,
или условие близости двух последовательных
приближений
Пример 3. Реализация итерационного метода Ньютона.
