Математическое описание вентильной машины

Математическое описание вентильной машины реализуется аналогично асинхронной машине.

Уравнения равновесия э.д.с на обмотках статора в неподвижной системе координат базируется на втором законе Кирхгофа (ротор не имеет обмоток) рис2.24.

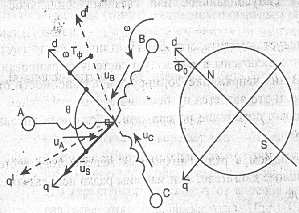
Рис.3.24. Функциональная схема ВМ.

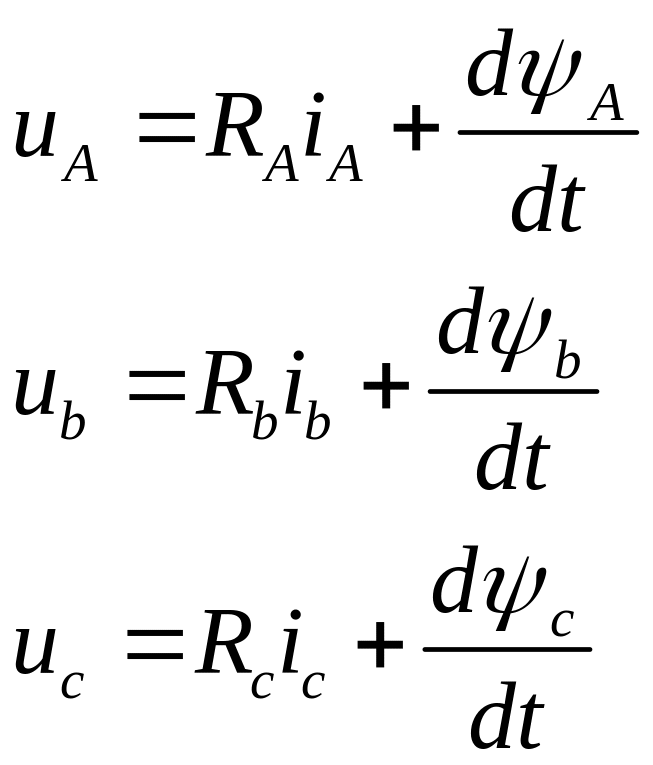(3.35)

Модель вентильной машины в неподвижной системе координат

Уравнения машины в неподвижной системе координат находится на основании уравнений (3.35) .

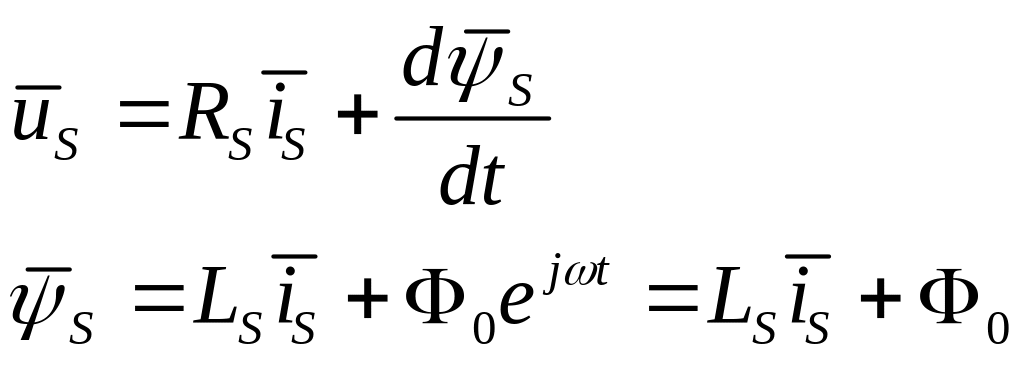
(3.36)

В уравнениях (3.36) значения проекций потока и напряжения на неподвижные оси координат α, β связаны между собой за счет датчика положения ротора ДПР, рис.3.35. в реверсионных электроприводах ДПР устанавливается таким образом, чтобы пространственных вектор напряжения был сдвинут на 90 эл.град. относительно пространственного вектора потока. В этом случае проекции пространственных векторов на оси α, β запишутся в виде:

(3.37)

Модель вентильной машины представлена на рис.3.25

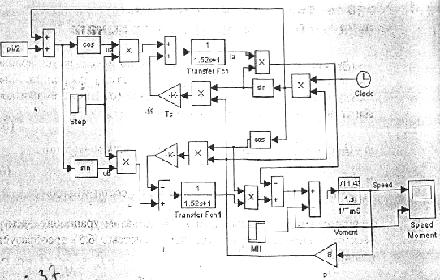
Рис. 3.25. Цифровая виртуальная модель ВМ в неподвижной системе координат .

SD ab1.

Модель вентильной машины во вращающейся системе координат

При анализе вентильной машины обычно используется вращающаяся со скоростью вращения ротора система координат.

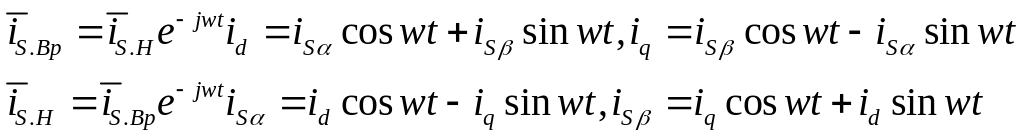(3.38)

При переходе к вращающимся координатам уравнение электрического равновесия (первое уравнение системы) преобразуется к виду:

(3.39)

Разложив результирующие вектора электромагнитных переменных состояния по осям, получим скалярное описание машины. При этом ось d совмещается осью потока ротора рис.3.36

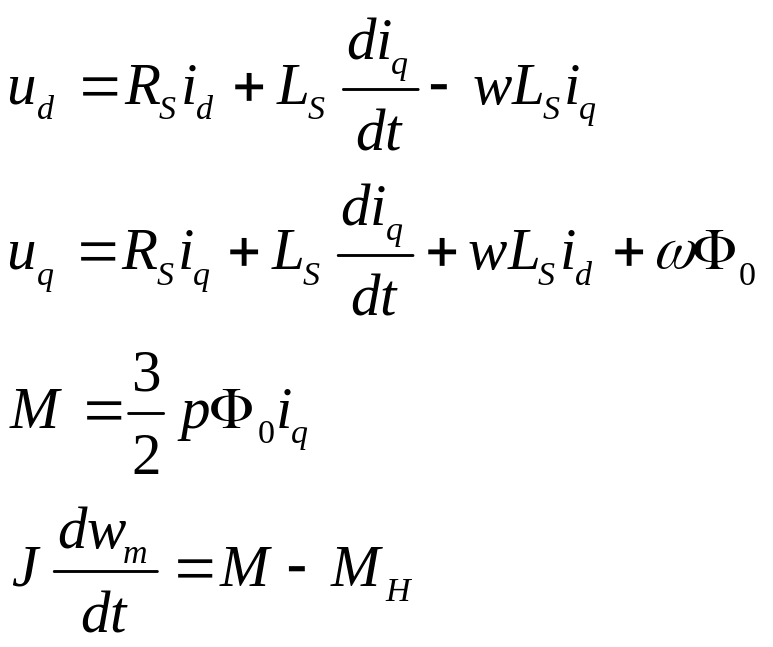(3.40)

При анализе вводятся относительно переменные.Модель вентильной машины во вращающейся системе координат представлена на рис.3.26

Рис.3.26 Цифровая виртуальная модель ВМ во вращающейся системе координат SD dq.

Модель вентильной машины во вращающейся системе координат с учетом запаздывания в канале вт-дм-ф.

Уравнения синхронной машины во вращающейся системе координат получены выше. Эти уравнения составлены для самой машины, они не учитывают влияние запаздывания в канале ВТ-ДМ-Ф. Для учета этого влияния определим напряжения U’d,U’q в системе координат d’,q’, тогда в относительных величинах получим:

Модель вентильной машины представлена на рис.3.27. Модель содержит соответственно синхронный двигатель и блок Subsystem, учитывающий запоздание в канале

ВТ-ДМ-Ф Моделирование осуществлено для двигателя ДБМ150-4-1.5-3 и датчика положения ротора типа ВТ60.

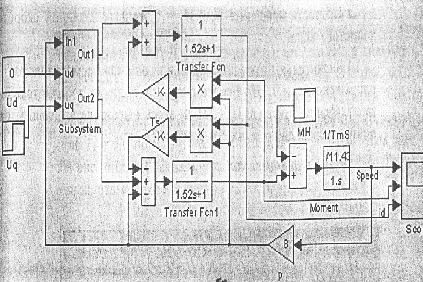
Рис.3.27. Цифровая виртуальная модель ВМ во вращающейся системе координат

с ВТ-ДМ-Ф SD dq1.