
Среднее Заочное отделение / 3 семестр / ТЭС / TES_Kr2
.pdfКонтрольная работа №2
Вариант 8
Задача 1 1.1. Напишите формулу ряда Котельникова и поясните смысл теоремы Котельникова.
При преобразовании аналогового сигнала в дискретный (процесс дискретизации) ин-
тервал следования отсчетов определяется теоремой Котельникова. Эта теорема формулируется следующим образом: если непрерывный сигнал u(t) имеет ограниченный спектр и наивысшая частота в спектре меньше, чем fв герц, то сигнал u(t) полностью определяется последовательно-
стью своих мгновенных значений в дискретные моменты времени, отстоящие друг от друга не
более, чем на |
1 |
секунд. |
2 × fв |
Всоответствии с этой теоремой сигнал с ограниченным спектром и верхней частотой
ωв ≤ ωд / 2 можно представить рядом
|
|
|
∞ |
sinωд ×(t - n ×Dt) |
|
|
|
|
u(t) = ∑u(n ×Dt) × |
|
|||
|
|
|
, |
(1) |
||
|
|
|
||||
|
|
|
n=−∞ |
ωд ×(t - n ×Dt) |
|
|
где u(n × Dt) , n = … -1,0,1, … - отсчеты мгновенных значений сигнала u(t), |
|
|||||
ωд = 2 ×π × fд , fд - частота дискретизации по времени, |
|
|||||
|
sin ωд |
× (t - n × Dt) |
|
|
|
|
|
|
|
- функция отсчета. |
|
|
|
|
ωд × |
|
|
|
|
|
|
(t - n × Dt) |
|
|
|
||
1.2. По заданным на рисунке 1 и в таблице 1 параметрам непрерывного сигнала и (t)
определите:
-интервал дискретизации t частоту дискретизации fД;
-число уровней квантования L;
-квантованные значения дискретных отсчётов непрерывного сигнала UКВ (t) для десяти отсчётов t по оси времени;
-величину ошибки квантования ε(t) ;
-число разрядов n в кодовой комбинации при кодировании двоичным кодом уровней квантования L;
-кодовые комбинации уровней квантования дискретных отсчётов.
1
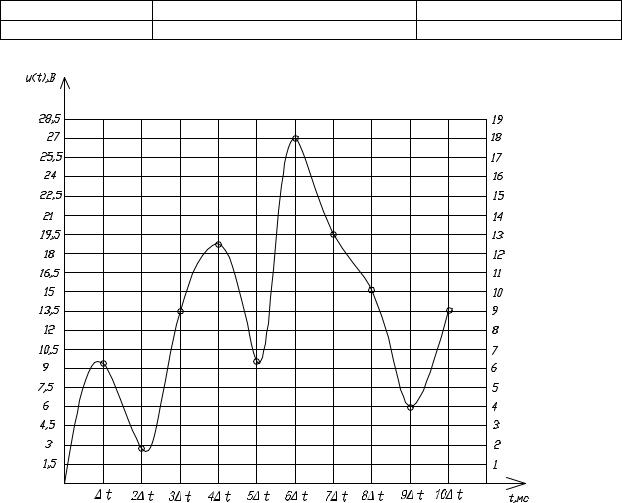
Таблица 1 – |
Исходные данные к задаче 1 |
|
|
|
|
Номер варианта |
Спектр сигнала Fmin…Fmax, |
кГц |
Шаг квантования |
U , мВ |
|
8 |
|
0,3…3,4 |
|
1,5 |
|
Рисунок 1 – Временная диаграмма непрерывного сигнала
Решение:
Определим интервал дискретизации по формуле
Dt £ 1/(2 × fmax ) |
(2) |
Dt £ 1/(2 × 3,4 ×103 ) = 147,1мкс
Определим частоту дискретизации по формуле
fд = 2 × FMAX |
(3) |
fд = 2 × 3,4 ×103 = 6,8кГц
2

Определим число уровней квантования по формуле
L = |
U max |
+1 |
(4) |
|
|||
|
U |
||
|
|
||
L = 27 +1 =19 уровней
1,5
Определим число разрядов в кодовой комбинации по формуле
n = log 2 L |
(5) |
n= log 2 19 = 5 разрядов
1.3.Все полученные результаты сведите в таблице 2 и постройте графики, поясняющие суть решения задачи.
Таблица 2 – Результаты решения задачи 1, пункт 3
Номер |
|
|
Шаг квантования U = 1,5 мВ |
|
|
отсчета |
U(t) АИМ, мВ |
UКВ(t) , мВ |
ε (t) , мВ |
Номер уровня квантования N |
Двоичный код |
1 |
10 |
9 |
1 |
6 |
00110 |
2 |
2,5 |
3 |
-0,5 |
2 |
00010 |
3 |
13,5 |
13,5 |
0 |
9 |
01001 |
4 |
19 |
18 |
1 |
12 |
01100 |
5 |
10 |
9 |
1 |
6 |
00110 |
6 |
27 |
27 |
0 |
18 |
10010 |
7 |
19,5 |
19,5 |
0 |
13 |
01101 |
8 |
15,5 |
15 |
0,5 |
10 |
01010 |
9 |
6 |
6 |
0 |
4 |
00100 |
10 |
13,5 |
13,5 |
0 |
9 |
01001 |
3
а)
б)
в)
г)
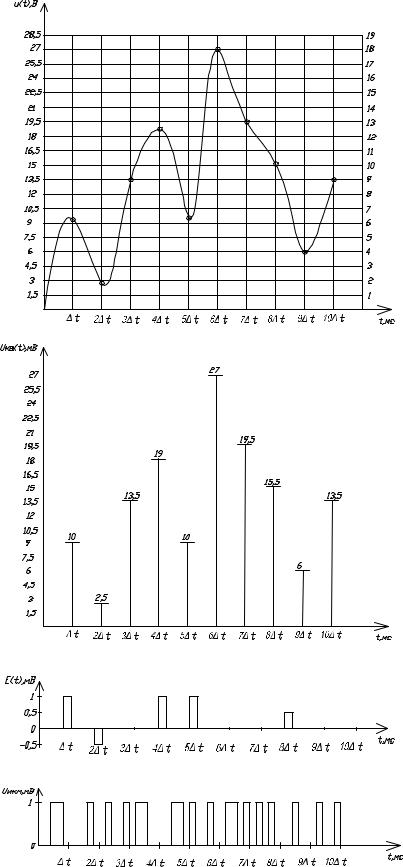
Рисунок 2 – Формирование ИКМ сигнала
а) исходный непрерывный сигнал; б) квантованные отсчеты; в) ошибка квантования; г) сигнал ИКМ.
4
Задание 2
2.1. Поясните сущность процесса детектирования сигналов. Начертите схему простей-
шего диодного детектора амплитудно-модулированных сигналов.
Процесс выделения модулирующего сигнала из высокочастотного модулированного колебания называется детектированием. Этот процесс является обратным модуляции, поэтому его часто называют демодуляцией.
Поскольку цель детектирования состоит в том, чтобы получить низкочастотный сигнал из модулированного колебания, спектр которого содержит только высокочастотные компонен-
ты, линейные цепи для детектирования непригодны. В большинстве случаев детекторы пред-
ставляют собой нелинейные цепи или реже — параметрические. Основное, требование, предъ-
являемое к детекторам AM сигналов, состоит в том, что постоянная составляющая тока или на-
пряжения на выходе детектора должна зависеть от амплитуды гармонического колебания на его входе. Если это требование выполняется и к детектору подводится AM сигнал sAM(t), постоян-
ная составляющая выходного тока будет меняться в соответствии с изменением модулирующе-
го напряжения u(t). Детектирование не будет приводить к искажениям, если изменение посто-
янной составляющей тока будет пропорционально изменению амплитуды сигнала sAM(t).
Изобразим схему диодного детектора АМ сигналов.
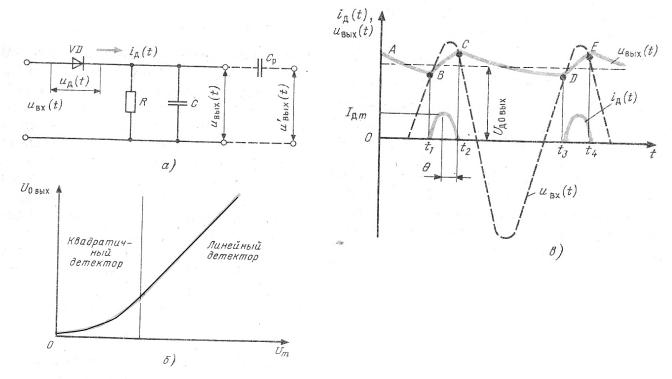
Рисунок 3 – Амплитудный диодный детектор: а) принципиальная схема;
б) характеристика детектирования; в) диаграммы выходного напряжения.
5
2.2. Для чего необходим нелинейный элемент при амплитудном детектировании? В чём отличие между линейным и квадратичным детектированием AM?
Так как линейные цепи для детектирования не пригодны, то детекторы представляют собой нелинейные цепи. Основным элементом такой цепи является полупроводниковый диод
(нелинейный элемент). Необходимость использования нелинейного элемента описана в пункте
2.1.
Квадратичный и линейный детекторы.
Если вольт-амперная характеристика нелинейного элемента детектора может быть ап-
проксимирована полиномом второй степени i(u)==a0+a1*u+a2*u2, то детектор называют квадра-
тичным. Указанная аппроксимация является достаточно точной только для небольших участков характеристики при малых амплитудах входного напряжения (в практических схемах — не бо-
лее 100...300 мВ). Основной недостаток квадратичного детектора — заметные нелинейные ис-
кажения продетектированного сигнала.
Линейными называются детекторы, у которых вольт-амперная характеристика нели-
нейного элемента может быть представлена как кусочно-линейная, состоящая из двух линей-
ных участков различной крутизны. Такая аппроксимация дает достаточно точные результаты только при входных воздействиях большой амплитуды. Детектирование в линейном детекторе осуществляется без искажений, если амплитуда входного напряжения превышает 500... 1000
мВ.
Подчеркнем, что детектор, схема которого изображена на рисунке 3, а, работает как квадратичный при малых входных сигналах и как линейный — при больших. Это подтвержда-
ется характеристикой детектирования, изображенной на рисунке 3, б. Данная характеристика представляет собой зависимость постоянной составляющей выходного напряжения U0 ВЫХ де-
тектора от амплитуды сигнала Um на входе. При малых амплитудах Um эта зависимость нели-
нейна (квадратичное детектирование), при больших — практически линейна (линейное детек-
тирование).
2.3. В схеме диодного детектора AM применён диод с крутизной вольтамперной ха-
рактеристики S = 10 мА/В. Согласно исходных данных (таблица 3), рассчитайте значения ёмко-
сти конденсатора Сн и определите коэффициент передачи детектора.
Таблица 3 – Исходные данные к задаче 2, пункт 3
Номер варианта |
Rн, кОм |
f0, кГц |
Fmax, кГц |
8 |
14 |
800 |
5 |
6
|
|
|
|
|
|
|
|
Решение: |
|
|
||
Рассчитаем емкость конденсатора. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
ω0 = 2 ×π × f0 |
|
(6) |
||
|
|
|
|
|
|
|
10 |
|
<< Rн |
|
(7) |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 ×π × f0 ×Cн |
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
5 |
>> |
5 |
|
|
=142,2пФ |
(8) |
|||
|
Сн >> π × f0 × Rн |
3,14×800×103 ×14×103 |
||||||||||
|
|
|
|
0,1 |
|
|
0,1 |
|
|
|||
С другой стороны С |
|
<< |
|
= |
|
= 227,5пФ |
(9) |
|||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2 ×3,14 ×5×103 ×14 ×103 |
||||||||
|
н |
|
2 ×π × Fmax × Rн |
|
|
|||||||
Таким образом, значение емкости конденсатора должно находится в пределах 142,2 × 10-12
… 227,5 × 10-12 Ф. Принимаем значение емкости конденсатора, как среднее значение между этими
двумя величинами
Сн |
= Cн |
+ |
Cнв −Cнн |
=142,2 + |
227,5 −142,2 |
=185пФ |
(10) |
|
|
||||||
|
|
2 |
2 |
|
|
||
Коэффициент передачи амплитудного детектора определяется следующим образом
Kд = cos |
3π /(Sср × Rн ) |
(11) |
Kд = cos 
 3 ×180 /(10 ×10−3 ×14 ×103 ) = 0,9994
3 ×180 /(10 ×10−3 ×14 ×103 ) = 0,9994
Ответ: Cн = 185 пФ; Kд ≈ 0,9994.
Задание 3
3.1. Дайте определение понятиям энтропия, производительность источника и пропуск-
ная способность канала.
Энтропия – среднее количество информации, создаваемое источником при выдаче од-
ного сообщения.
7
Производительность источника – среднее количество информации, создаваемое источ-
ником в единицу времени.
Пропускная способность канала – наибольшая скорость передачи информации по кана-
лу при заданных ограничениях.
3.2. Перечислите свойства энтропии. Поясните каждое из перечисленных свойств.
Свойства энтропии:
а) энтропия равна нулю, если вероятность появления одного сообщения равна единице
(т.е. оно достоверно), а другие сообщения невозможны, т.е. вероятность их появления равна ну-
лю;
б) энтропия максимальна, когда все сообщения равновероятны и их количество растет;
в) энтропия обладает свойством аддитивности, т.е. энтропия различных источников может складываться.
3.3. Найти пропускную способность m-ичного симметричного канала без памяти и сти-
рания по числовым значениям, приведённым в таблице 4.
Таблица 4 – Исходные данные к задаче 3, пункт 3
Номер варианта |
В, Бод |
m |
p |
8 |
1000 |
3 |
0,01 |
Решение
Пропускная способность m-ичного симметричного канала без памяти и стирания опре-
делим по формуле
C |
|
= B ×[log |
|
m + p × log |
|
p |
|
+ (1 - p) × log |
|
(1 - p)] , |
(12) |
|
н |
2 |
2 m -1 |
2 |
|||||||||
|
|
|
|
|
|
|||||||
где В – техническая скорость, Бод;
m – основание кода;
p – вероятность появления.
C |
|
= 1000 ×[log |
|
3 + 0,01× log |
|
0,01 |
+ (1 - 0,01) × log |
|
(1 - 0,01)] = 1494,2бит / с |
|
|
|
|
|
|||||
|
н |
|
2 |
|
2 3 -1 |
2 |
|
||
Ответ: 1494,2 бит/с.
8
Задание 4
4.1.Дайте определение понятия помехоустойчивости.
Помехоустойчивость – способность системы передачи информации выполнять свои функции при наличии помех, т.е. противостоять мешающему действию помех.
4.2.Что понимают под потенциальной и реальной помехоустойчивостями систем связи?
Потенциальная помехоустойчивость – помехоустойчивость, при которой возможная вероятность ошибки при заданных условиях является минимальной.
Потенциальная помехоустойчивость не является характеристикой конкретной системы передачи сообщений, а определяется лишь условиями передачи и приема сигналов (видом мо-
дулирующего сигнала, способом модуляции, свойствами помехи и канала передачи).
Вероятность ошибки можно вычислить для каждой конкретной системы передачи дис-
кретных сообщений; она и будет характеризовать реальную помехоустойчивость данной систе-
мы. Ее значение, как правило, оказывается ниже потенциальной помехоустойчивости. Разница между ними характеризует возможность повышения качества передачи информации в этих ус-
ловиях путем совершенствования системы передачи.
4.3.Согласно исходных данных (таблица 5), вычислите вероятность ошибки Pот опти-
мального приёма сигналов двоичной ОФМ при неопределённой фазе сигнала. Как изменится вероятность ошибки при увеличении скорости модуляции В в два раза?
Таблица 5 – Исходные данные к задаче 4, пункт 3
Номер варианта |
РС, мВт |
F, кГц |
N0, Вт/Гц |
8 |
2,4 |
350 |
5*10-7 |
Решение
Вероятность ошибки оптимального приема сигналов двоичной ОФМ при неопределен-
ной фазе определяется по формуле
Pош = 0,5 × e−h2 , (13)
9

где h2 = E − отношение энергии сигнала к спектральной плотности мощности шума.
N0
Определим энергию сигнала по формуле
E = P ×T = |
Pc |
|
(14) |
|||||
|
|
|
||||||
|
c |
|
F |
|
||||
|
|
|
|
|
||||
Следовательно, формула (11) примет вид: |
|
|
|
|
|
|
||
P = 0,5 × e- |
|
Pc |
|
|
|
|||
F×N0 |
|
|
(15) |
|||||
ош |
|
|
|
|
|
|
|
|
P = 0,5 × e- |
2,4×10−3 |
|
|
|
|
|
|
|
350×103×5×10−7 |
= 0,4932 |
|
||||||
ош |
|
|
|
|
|
|
|
|
При увеличении скорости модуляции В в 2 раза вероятность ошибки определим по формуле
P'ош = 0,5×e- |
Pc |
|
||
2×F×N0 |
(16) |
|||
P'ош = 0,5 × e- |
2,4×10−3 |
|
||
2×350×103×5×10−7 |
|
= 0,4966 |
||
Вероятность ошибки при увеличении скорости модуляции В в 2 раза увеличится.
Ответ: Pош = 0,4932 ; P 'ош = 0,4966 .
Задача 5
5.1. Какой код является корректирующим? Перечислите основные параметры этих ко-
дов.
Корректирующий код – код, который способен обнаруживать и исправлять ошибки.
Основные параметры корректирующих кодов:
10
