Среднее Заочное отделение / 3 семестр / ОКМЭЦ / ОКМЭЦ_Василевский6

МИНИСТЕРСТВО СВЯЗИ И ИНФОРМАТИЗАЦИИ

РЕСПУБЛИКИ БЕЛАРУСЬ

Учреждение образования

"ВЫСШИЙ ГОСУДАРСТВЕННЫЙ КОЛЛЕДЖ СВЯЗИ"

КОНТРОЛЬАЯ РАБОТА № 1

по дисциплине: " Основы компьютерного моделирования электрических цепей "

Выполнил: студент

Проверил: Бондаренко В.Ф.

МИНСК 2017

Задание № 1

Ввести и вычислить арифметическое выражение

Требуется занести в выражение значения переменных x = -1,5∙10^-2, y = 2,2π и вычислить его. Проконтролировать с помощью команды pretty ввод выражения. Отобразить результат вычисления в различных форматах.

Вариант № 6

C = ctg

Решение:

Задание № 2

Вычислить матричное выражение

Ввести матрицы

А = , B = , C =

и найти значение заданного выражения. Если результат не целочисленный, отобразить его в формате rat. Изучить информацию о переменных при помощи команды whos. Открыть окно для просмотра переменных рабочей среды Workspace. Заменить с использованием редактора Array Editor матрицы A, B, C на новые

А = , B = , C = ,

и повторить вычисления.

Вариант № 6

(BCB−2C^T)A²

Решение:

Изучение информации о переменных при помощи команды whos:

Изменение матриц:

Вычисление с новыми данными :

Задание № 3

Решить систему линейных алгебраических уравнений

Дана система линейных алгебраических уравнений Ах = в. Вычислить определитель │А│. Если │А│ ≠ 0, решить систему с помощью оператора обратного деления < \ >. Проверить решение подстановкой. Вычислить обратную матрицу А^-1 и решить систему с помощью с помощью обратной матрицы. Если полученное решение приближенное, повторить вычисления в формате rat.

Вариант № 6

Решение:

Вычисление с помощью обратной матрицы А^-1

Задание № 4

Создание векторов и применение к ним математических операций и команд обработки данных

Для заданных векторов a и b длины n:

1. вычислить их сумму, разность и скалярное произведение;

2. образовать вектор с =[a₁,a₂,…,a_n,b₁,b₂,…,b_n], определить его максимальный и минимальный элементы и поменять их местами;

3. упорядочить вектор c по возрастанию и убыванию;

4. переставить элементы вектора c в обратном порядке и записать результат в новый вектор (с помощью rot90);

5. найти векторное произведение u=[a₂,a₅,a₆] и v=[b₁,b₃,b₅] (с помощью cross).

Вариант № 6

a = [3.5 6.8 -7.1 6.8 -5.0 -2.3 -4.4 -0.2]; b = [5.5 1.5 5.7 -4.6 -2.3 -5.3 5.5 2.3].

Решение:

1. вычисление суммы, разности и скалярного произведения для заданных векторов a и b длины n

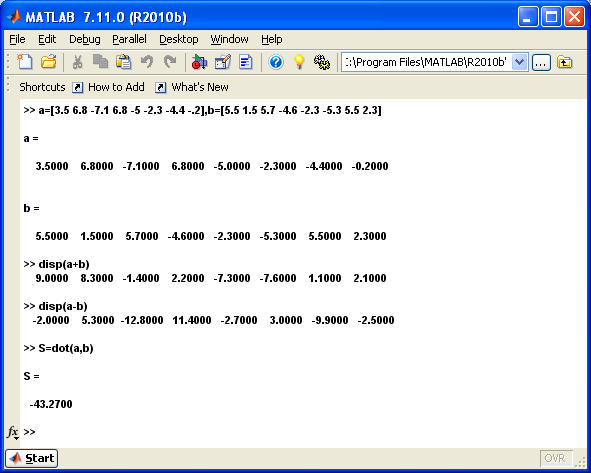
2. образование вектора с =[a₁,a₂,…,a_n,b₁,b₂,…,b_n], определение его максимального и минимального элементов и замена их местами

3. упорядочение вектора c по возрастанию и убыванию

4. перестановка элементов вектора c в обратном порядке и запись результата в новый вектор (с помощью rot90)

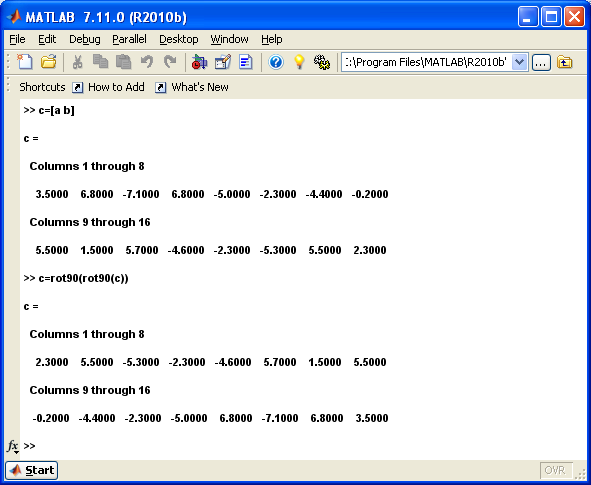
5. нахождение векторного произведения u=[a₂,a₅,a₆] и v=[b₁,b₃,b₅] (с помощью cross)

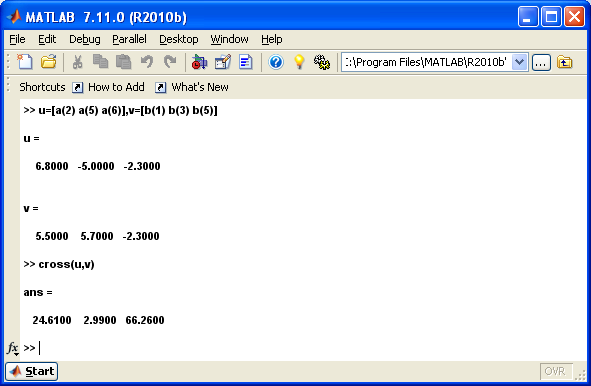
Задание № 5

Создать матрицу и применить команды обработки данных и поэлементных операций для нахождения заданных величин

Сконструировать при помощи команд создания специльных матриц, индексации двоеточием и, возможно, поворота, транспонирования или вычеркивания следующие матрицы и применить команды обработки данных и поэлементные операции для нахождения заданных величин.

Вариант № 6

A=

Решение:

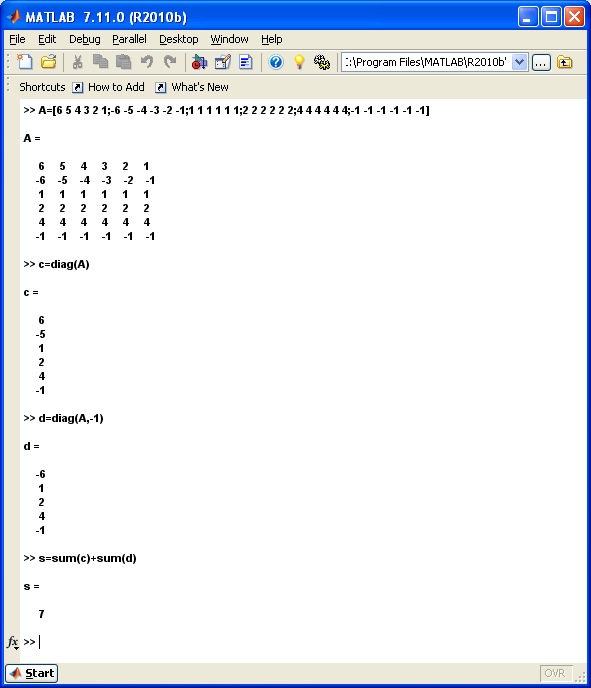
Задание № 6

Найти собственные числа и векторы матрицы, ее характеристический полином, ранг и определитель

Для матрицы A из соответствующего варианта Задания 5 найти собственные числа и векторы матрицы A, ее характеристический полином, ранг и определитель.

Вариант № 6

A=

Решение:

Находим характеристический полином

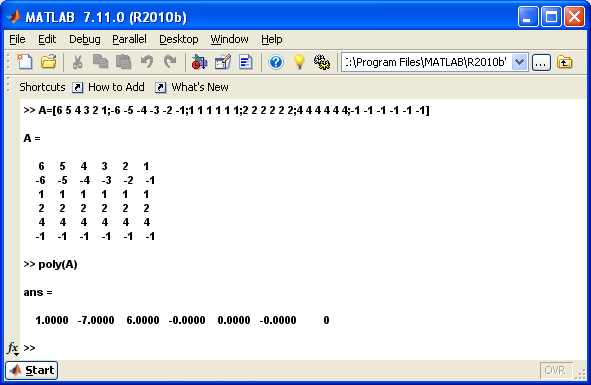
Находим собственные числа и векторы матрицы A

Находим ранг и определитель

Задание № 11

Построить график функции с применением команды plot(t,y)

При построении графикa вид функции, пределы, шаг изменения аргумента выбрать с использованием следующих данных.

Вариант № 6

Вариант	Функция	Интервал задания, шаг дискретизации
6	y(t)=etcos2(20t)	t[0;2], Δt=0,01

Решение:

Задание № 12

Построить в одном окне графики двух функций y₁(t) и y₂(t) с использованием команды plotyy(…)

При построении графиков вид функций, пределы, шаг изменения аргумента выбрать с использованием следующих данных.

Вариант № 6

Вариант	Функция		Интервал задания, шаг дискретизации
6	y1(t)=10, y2(t)= (20t)	t=[0;1], ∆t=0,01

Решение:

Задание № 13

С помощью команды plot(t,y1,'S1′,t,y2,′S2′) построить в одном окне графики двух функций y₁(t) и y₂(t)

При построении графиков вид функций, пределы, шаг изменения аргумента и параметр ‘S’ выбрать с использованием следующих данных.

Вариант № 6

Ва-ри-ант	Функции, интервал задания, шаг дискретизации	Параметры (цвет линии, тип маркера, тип линии)
6	y1(t)=0,1, t[0;2], ∆t=0,2	Голубой, треугольник вершиной вниз, сплошная
	y2(t)=60(2t), t[0;2], ∆t=0,2	Красный, треугольник вершиной вверх, пунктирная

Решение:

Задание № 21

С помощью команд mesh(…) и surfc(…) построить каркасную поверхность, заданную функцией z(x,y), и соответствующий этой поверхности контурный график

С помощью команды colorbar установить соответствие между цветом и значениями функции на каркасной поверхности. Функцию z выбрать в соответствии со своим вариантом.При построении графика использовать координатную сетку.

Вариант № 6

Вари- ант	Координаты сетки матрицы аргументов [x,y]=meshgrid(…);	Вид функции
6	(-3*pi:0.3*pi:3*pi)

Решение:

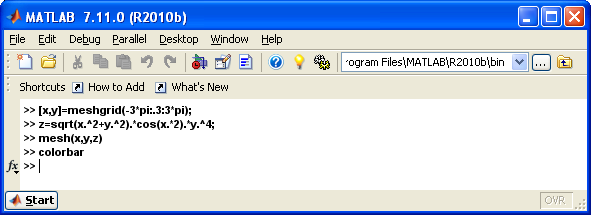
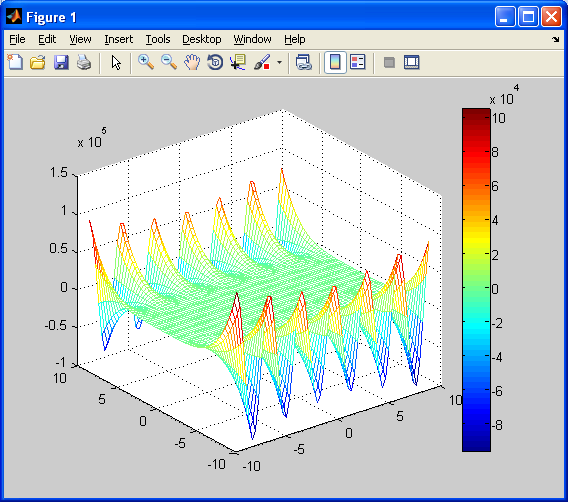
Задание № 22

С помощью команды surfl(…) и команды shading interp построить плавно залитую цветом поверхность, заданную функцией z(x,y)

Цветовую палитру окраски поверхности выбрать с помощью команды colormap(…) и таблицы, которая приведена ниже, добившись наиболее реалистичного вида поверхности.

С применением команды colorbar установить соответствие между цветом и значениями функции на каркасной поверхности. Функцию z выбрать в соответствии со своим вариантом.

Вариант № 6

Вари- ант	Координаты сетки матрицы аргументов [x,y]=meshgrid(…);	Вид функции
6	(-3*pi:0.3*pi:3*pi)
	Палитра	Изменение цвета
	gray	Оттенки серого

Решение:

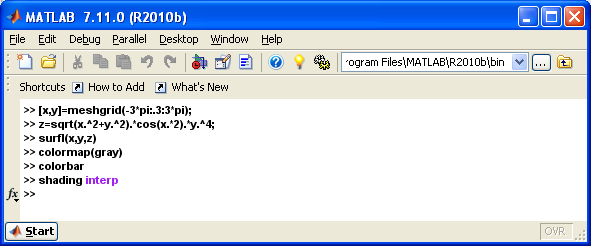
Задание № 23

Найти предел

Вариант № 6

Решение:

Задание № 24

Найти производные

Найти первые и вторые частные производные функции двух переменных f(x,y). Проверить выполнение условия f''_xy(x,y) = f''_yx(x,y). Вычислить градиент функции f(x,y) в точке (1;2).

Вариант № 6

f(x,y) = sinx^cosy

Решение:

Задание № 25

Найти неопределенный интеграл

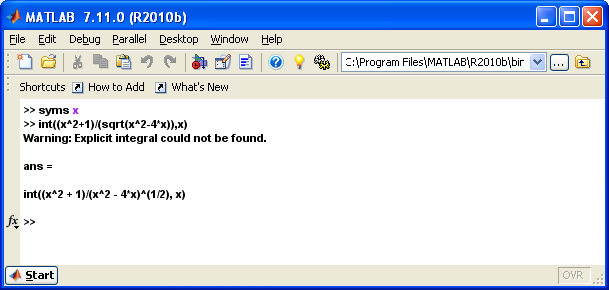
Найти неопределенный интеграл dx. Воспользоваться при необходимости командами pretty, simple.

Вариант № 6

dx

Решение:

Литература

1. Бондаренко В. Ф. MatLab. Основы работы и программирования, компьютерная математика. Учебн. курс. / В. Ф. Бондаренко, В. Д. Дубовец. – Минск. Харвест. 2010. – 256 с.

2. Бондаренко В. Ф., Дубовец В. Д. Электронный конспект лекций «TROPA V MATLAB_21.doc».

29.10.2013 _________