Контрольная работа

Задача 1

Для повышения точности проведена серия измерений одного и того же значения. Полученные результаты приведены в таблице 1. Определить наиболее достоверное значение величины, абсолютную и относительную погрешность каждого из измерений, среднеквадратическую погрешность результата измерений. Записать результат измерений с учетом этой погрешности и доверительной вероятности.

Таблица 1 – Исходные данные к задаче 1

Вариант	Единицы измерения			Номер и результаты измерения											Доверительная вероятность
		1	2	3	4	5	6	7	8	9		10
10	пФ	460	509	490	485	505	501	498	500	483		469		0,8

Решение:

Если проведено 10 измерений одной и той же величины при неизменных внешних условиях, то наиболее достоверным значением является С_ср.

C +C +C +C +C +C +C +C +C +C (1)

_Cср =,

где С₁, С₂ ,…, С₁₀ – результаты измерений величины С.

460+509+490+485+505+501+498+500+483+469

Cср = 10 =490пФ

Абсолютная погрешность определяется по формуле

∆С_i =С_i −С_д, (2)

где С_i – показания прибора;

С_д – действительное значение (С_д = С_ср).

∆С₁ =460−490=−30пФ

∆С₂ =509−490=19пФ

∆С₃ = 490 − 490 = 0пФ

∆С₄ =485−490=−5пФ

∆С₅ = 505− 490 =15пФ

∆С₆ = 501− 490 =11пФ ∆С₇ = 498− 490 = 8пФ

∆С₈ = 500 − 490 =10пФ

∆С₉ = 483− 490 = −7пФ

∆С₁₀ = 469 − 490 = −21пФ

Относительная погрешность определяется по формуле:

∆Cⁱ δ= ⋅100% (3)

C_i

% 2,2%

% %

0% 2,0%

% %

% %

Среднеквадратическая погрешность определяется по формуле:

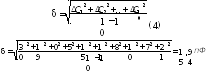
Результат измерения с учетом доверительной вероятности записывается в виде

С_изм =С_д −E, (5)

где Е – доверительный интервал с учетом доверительной вероятности. Доверительный интервал определяется по формуле

E 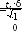, (6)

гдеt_r– коэффициент, зависящий от величины доверительной вероятности.

E 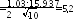пФ

С_изм = (490±5,2)пФ

Ответ: С_изм = (490±5,2)пФ.

Задача 2

Стрелочным вольтметром с равномерной шкалой класса точности К и предельным значением шкалы U_к измерены величины трех напряжений U₁, U₂, U₃. Какое из указанных напряжений измерено более точно? Чему равна абсолютная и относительная погрешность каждого измерения? Построить график изменения величины относительной погрешности заданного прибора в координатах. Дать рекомендации по использованию измерительного прибора.

Таблица 2 – Исходные данные к задаче 2

Параметр	k	Uk, В	U1, В	U2, В	U3, В
Значение для В-10	2,5	30	15	30	20

Решение:

Определим абсолютную погрешность измерений

k ⋅U^k

∆U = (7)

100

В

Определим относительную погрешность каждого измерения

∆U

δ_i = ⋅100%

U1 (8)

0,75 δ₁ = ⋅100% = 5%

15

2,5%

%

Наиболее точно измерено то напряжение, у которого относительная погрешность наименьшая, т.е. U₂ = 30 В. Построим график изменения величины относительной погрешности заданного прибора в координатах.

Рисунок 1 – График изменения величины относительной погрешности

Данный вольтметр измеряет значения напряжения достаточно близкие к предельному значению шкалы Uк.

Задача 3

Определить уровень по напряжению, если известен уровень по мощности L_M на рези-

сторе R, Ом.

Таблица 3 – Исходные данные к задаче 3

Вариант	10
LM, дБ	4
R, Ом	100