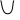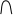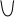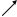Решение.
Область существования.
определена
в точке
,
если в точке (
,
)
существует касательная к графику, и
она не вертикальна. Следовательно:
D( ) = (–, –5) (–5, 0) (0, 1) (1, 3) (3, +).
Нули, интервалы знакопостоянства, разрывы.
х |
(–, –6) |
–6 |
(–6, –5) |
–5 |
(–5,–4) |
–4 |
(–4, 0) |
|
|
гладкий минимум |
|
касательная к графику вертикальна |
|
гладкий максимум |
|
|
< 0 |
= 0 |
> 0 |
разрыв 2-го рода
|
> 0 |
= 0 |
< 0 |
х |
0 |
(0, 1) |
1 |
(1, 3) |
3 |
(3,+) |
|
неустрани-мый разрыв 1-го рода |
|
разрыв 2-го рода |
|
негладкий минимум |
|
|
устранимый разрыв
|
< 0 |
разрыв 2-го рода
|
< 0 |
разрыв 1-го рода
|
> 0 |
Вертикальные и горизонтальные асимптоты.
Вертикальные: х = –5, х = 1.
Горизонтальные:
,
при х
– ;
,
при х
+ .
Интервалы монотонности и экстремумы.
х |
(-,–5) |
–5 |
(–5,–2) |
–2 |
(–2, 0) |
0 |
: направление выпуклости; точки перегиба |
вниз
|
перегиб на вертикали |
вверх
|
перегиб гладкий (наклон) |
вниз
|
разрыв
|
|
0 |
не сущ |
0 |
0 |
0 |
не сущ |
|
|
не сущ |
|
минимум –2 |
|
не сущ |
х |
(0, 1) |
1 |
(1, 3) |
3 |
(3, +) |
: направление выпуклости; точки перегиба |
вверх
|
разрыв
|
Вниз
|
перегиб с изломом |
вверх
|
|
0 |
не сущ |
0 |
не сущ |
0 |
|
|
не сущ |
|
не сущ |
|
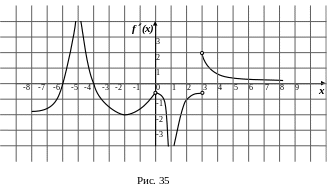
График
функции
представлен на рисунке 35.
