3. Примеры решения задач типового расчета

Пример 1. Найдите производную данных функций:

а) ; б) ; в) ;

г) ; д) ; е) .

Решение.

а) Данная функция – сложная, воспользуемся последовательно формулами: производная дроби, производная степенной функции:

.

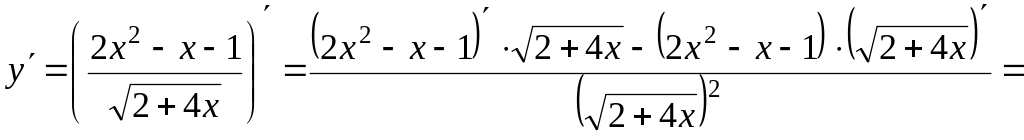
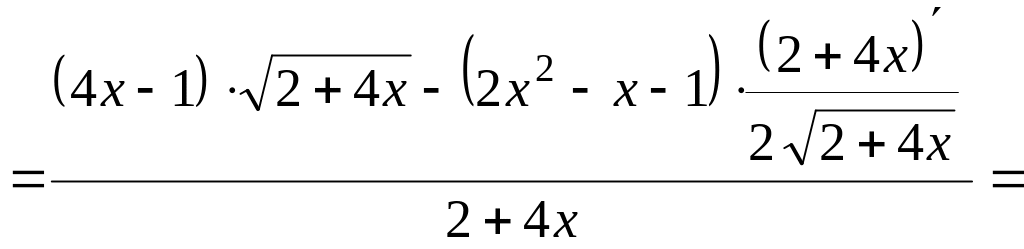
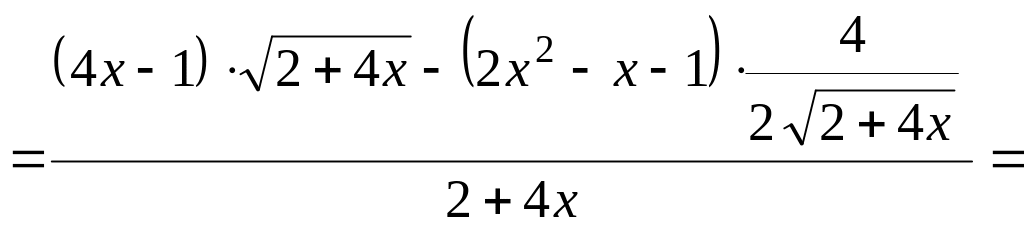
Ответ: .

б) Данная функция – сложная, воспользуемся последовательно формулами: производная логарифма, производная синуса, производная степенной функции.

.

Ответ: .

в) Преобразуем квадратный корень в степень:

.

Данная функция – сложная, воспользуемся последовательно формулами: производная степенной функции, производная дроби, производная логарифма.

= =

= = .

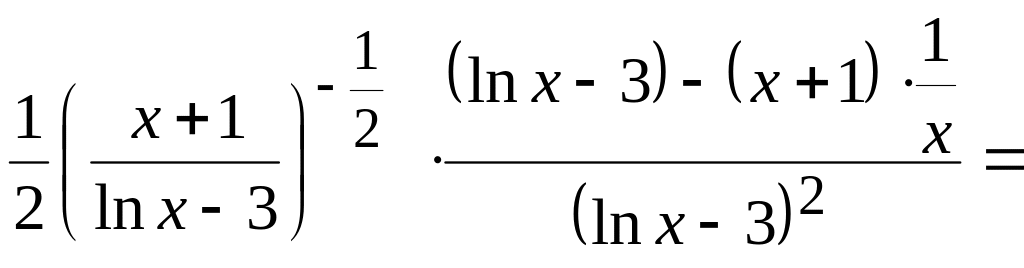
Ответ: .

г) Данная функция относится к виду показательно-степенной функции . Для нахождения ее производной прологарифмируем данную функцию:

.

Дифференцируем левую и правую часть этого равенства, при этом в левой части используем производную сложной функции, а в правой – производную произведения:

.

Решаем полученное уравнение относительно :

.

Заменяя , получим

.

Ответ: .

д) Данная функция задана неявно. Находим производную от левой части равенства, рассматривая при этом у как функцию от х. ;

;

;

.

Затем из полученного равенства выражаем искомую производную

.

Ответ: .

е) Данная функция задана параметрически. Производная данной функции находится по формуле . Продифференцируем по переменной t:

,

.

Тогда .

Ответ: .

Пример 2. Составьте формулу Тейлора с остаточным членом в форме Лагранжа для функции в точке .

Решение.

Формула Тейлора с остаточным членом в форме Лагранжа для произвольной функции имеет вид

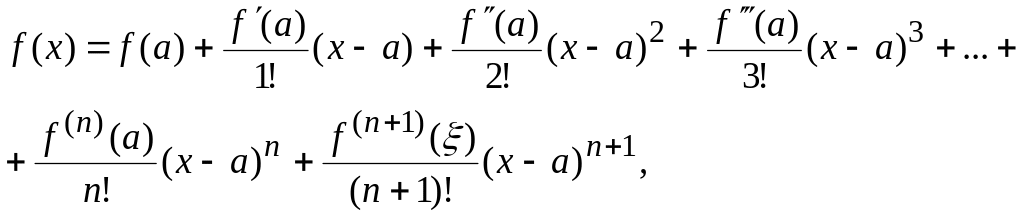
где , .

Для составления формулы Тейлора найдем производные данной функции до n -го порядка включительно и их значения в точке :

,

,

,

,

…

,

,

,

,

,

,

…

.

.

Найдем производную (n + 1)-го порядка для остаточного член в форме Лагранжа:

Тогда

, где

.

Ответ:

, .

Пример 3. Найдите наибольшее и наименьшее значения функции на отрезке .

Решение.

Наибольшее и наименьшее значение на отрезке функция может достигать:

1) в критических точках, если они существуют и принадлежат ;

2) на концах отрезка (т.е. при или ).

1. Найдем критические точки. Для этого найдем и решим уравнение .

;

; ; , ; .

2. Найдем и выберем из них наибольшее и наименьшее значения:

;

;

.

Ответ: – наибольшее значение функции на ;

– наименьшее значение функции на .

Пример 4. Провести полное исследование функции и построить ее график.

а) .

Решение:

1. Область определения.

Исключим точку, в которой знаменатель дроби , т. е. .

Таким образом, .

2. Четность, нечетность, периодичность функции.

 , .

Следовательно, данная функция не является ни четной, ни нечетной.

Так как в состав функции не входят периодические функции, то непериодическая.

3. Непрерывность.

Так как заданная функция является элементарной, то она непрерывна на своей области определения. Единственной точкой, в которой функция не существует, является точка .

Исследуем характер разрыва функции в этой точке.

;

.

Т.к. и левый, и правый пределы не являются конечными, то точка есть точка разрыва 2-го рода.

4. Асимптоты.

а) При функция терпит разрыв 2-го рода, значит прямая вертикальная асимптота.

б) Найдем наклонные асимптоты:

;

.

Прямая наклонная асимптота.

5. Нули функции и интервалы знакопостоянства.

Функция обращается в нуль при . Разобьем всю числовую прямую на интервалы точками , и определим интервалы знакопостоянства функции:

	–	+	+

Функция отрицательна на интервале и положительна на интервалах .

6. Интервалы монотонности и экстремумы.

Найдем критические точки.

;

, если критические точки.

не существует при , но эта точка не является критической, потому что функция в ней не определена.

Разобьем всю числовую прямую на интервалы точками , и , и определим знак производной на этих интервалах:

	(–, –6)	–6	(–6, –3)	–3	(–3, 0)	0	(0, +)
	+	0	–	не сущ	–	0	+
		–12 max		точка разрыва		0 min

Функция возрастает в интервалах (–, –6) и (0, +), убывает в интервалах (–6, –3) и (–3, 0), – максимум функции, – минимум функции.

7. Выпуклость, вогнутость, точки перегиба.

Найдем точки перегиба:

,  .

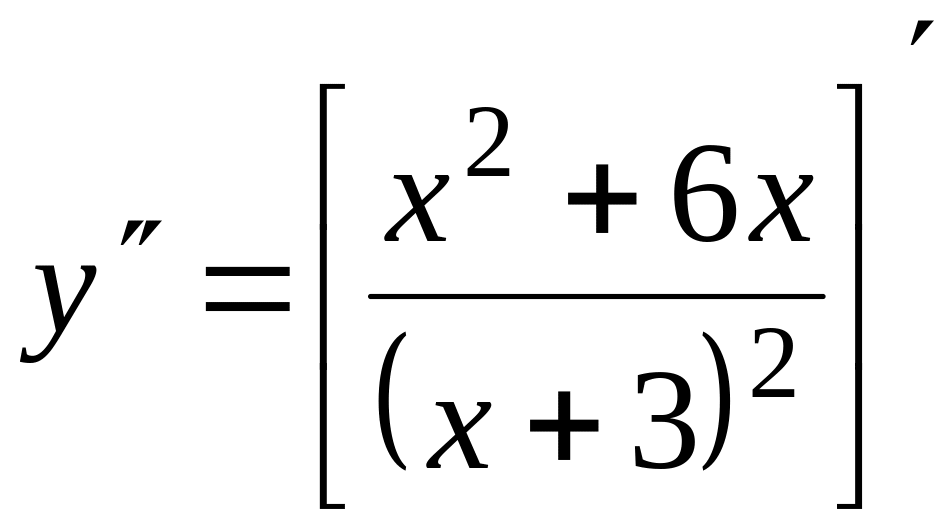
Следовательно, в точек перегиба нет. Исследуем выпуклость и вогнутость графика слева и справа от точки разрыва . Для этого определим интервалы знакопостоянства второй производной :

	(–, –3)	–3	(–3, +)
	–	не сущ	+
	выпукла	не сущ	вогнута

8. Построение графика (см. рис. 31).

9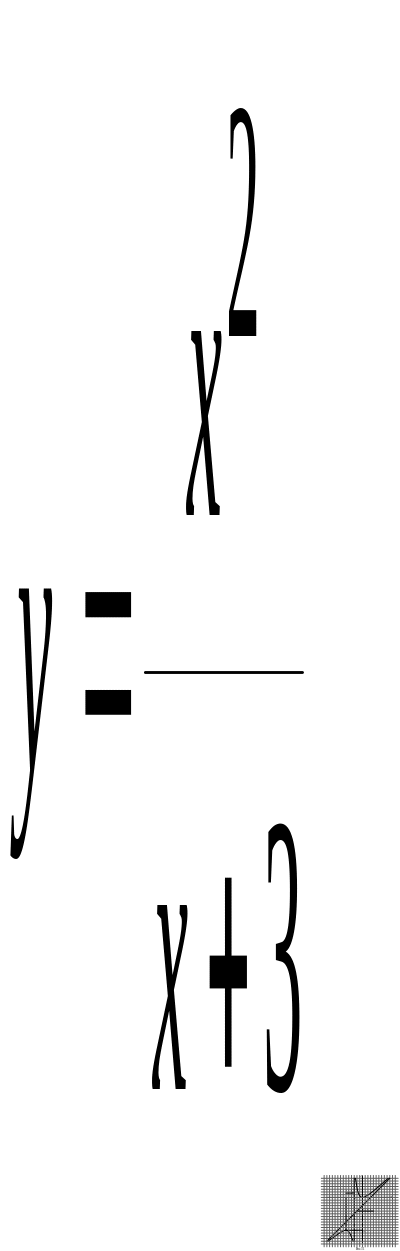 . Область значений. На основании построенного графика получаем, что .

б) .