IV. Нерівність виду

Дана нерівність рівносильна такій сукупності:

Приклад 6.

Розв’язати нерівність:

Розв’язання

Нерівність виконується в кожній точці, що належить області допустимих значень, бо права частина нерівності від’ємна. Областю допустимих значень даної нерівності є всі точки числової осі, крім х= 3.

Відповідь: х

Приклад 7.

Розв’язати нерівність:

Розв’язання

Задана нерівність з модулем рівносильна сукупності трьох систем нерівностей:

Розв’язок якої знаходимо об’єднанням проміжків, що є розв’язками системи цієї сукупності.

Відповідь:

V. Нерівність виду

Схеми розв’язання відповідних нерівностей:

1.

2.

3.

4.

Приклад 8.

Розв’язати нерівність:

Розв’язання

Піднесемо обидві частини цієї нерівності до квадрата і подамо отриману рівносильну нерівність у вигляді різниці квадратів:

Застосуємо формулу різниці квадратів двох виразів, звідки одержимо рівносильну нерівність:

Або

Коренями лівої частини нерівності є множина чисел , де корінь 1 є двократним. За допомогою «змійки» знаходимо розв’язок вихідної нерівності.

Відповідь:

Приклад 9.

Розв’язати нерівність:

Розв’язання

Оскільки обидві частини нерівності додатні, то при вона рівносильна такій нерівності:

Звівши останню нерівність до квадрата й перенісши всі члени в ліву частину, після перетворень за формулою різниці квадратів, одержимо нерівність:

Розв’язуючи яку, знаходимо відповідь.

Відповідь:

VI. Застосування заміни змінної в нерівностях.

Завдання подані в цьому розділі можуть бути розв’язані методом інтервалів для нерівностей, однак застосувавши відповідні заміни дістатися результату можна швидше.

Приклад 10.

Розв’язати нерівність:

Розв’язання

Покладемо тоді нерівність набуде вигляду:

Оскільки при усіх то Повертаючись до вихідної змінної, маємо:

Відповідь:

VII. Нерівності виду , що розв’язуються

розкладанням лівої частини на множники.

Приклад 11.

Розв’язати нерівність:

Розв’язання

Відповідь:

Приклад 12.

Розв’язати нерівність:

Розв’язання

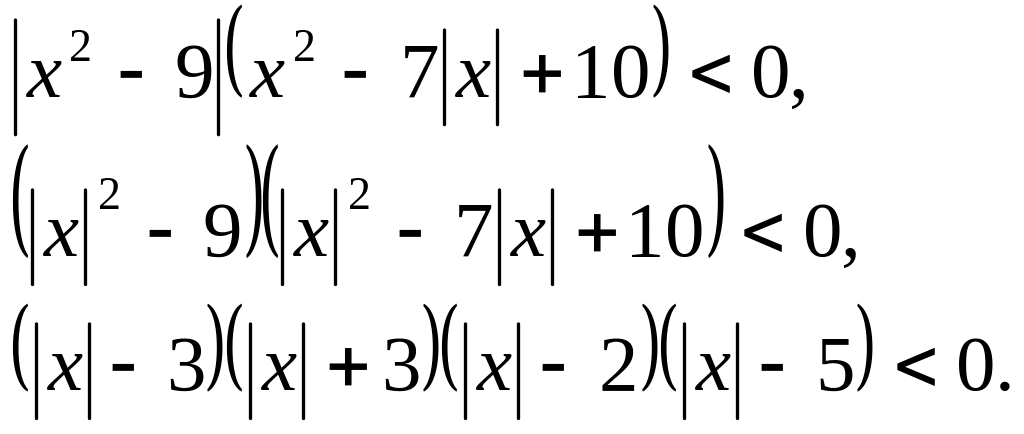
Нехай тоді нерівність має вигляд:

Отже, З огляду на те, що маємо сукупність нерівностей:

Відповідь:

VIII. Дробово – раціональні нерівності з невід’ємним

знаменником.

Приклад 13.

Знайти найменше від’ємне ціле значення х, що задовольняє нерівність:

Розв’язання

Область визначення нерівності Помноживши обидві частини нерівності на знаменник, одержимо:

З урахуванням умови маємо:

Відповідь: -2.

IX. Нерівності зі складним модулем.

Приклад 14.

Розв’язати нерівність:

Розв’язання

Розкриємо внутрішній модуль. Якщо то нерівність набуде вигляду:

Враховуючи область, яку розглянули,

Якщо то маємо:

Враховуючи область, яку розглянули, Поєднуючи розв’язки в обох проміжках, одержуємо відповідь. Відповідь:

Приклад 15.

Розв’язати нерівність:

Розв’язання

Областю визначення даної нерівності є :

Використовуючи основну властивість логарифмів, маємо:

Відповідь:

Нерівності для самостійного розв’язання.

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.