Зміст роботи.
І. Рівняння, системи рівнянь, нерівності та системи нерівностей, які містять знак абсолютної величини. Теоретичні відомості.
ІІ. Рівняння.
- Завдання для самостійного розв’язання.
ІІІ. Нерівності.
1. Нерівності загального виду.
2.
Нерівності виду
або
.
3.
Нерівності
виду
.
4.
Нерівність виду
.
5. Нерівність виду
6. Застосування заміни змінної в нерівностях.
7.
Нерівності виду
,
що розв’язуються розкладанням лівої
частини на
множники.
8. Дробово – раціональні нерівності з невід’ємним знаменником.
9. Нерівності зі складним модулем.
- Завдання для самостійного розв’язання.
IV. Рівняння і нерівності з параметрами, що містять знак абсолютної величини.
- Завдання для самостійного розв’язання
V. Системи рівнянь що містять абсолютну величину і параметри.
- Завдання для самостійного розв’язання.
VI. Використання властивостей модуля до розв’язування нестандартних завдань.
- Завдання для самостійного розв’язання.
§ І.Рівняння, системи рівнянь, нерівності та
системи нерівностей, які містять знак
абсолютної величини.
Теоретичні відомості.
А
бсолютна
величина (модуль) числа а позначається
.
Означення
=
a,
a
-а,
а
Властивості абсолютної величини числа:
1.
2.
3.
4.
5.
Часто при розв’язуванні рівнянь та нерівностей користуються наступними властивостями модуля:
6.
7.
8.
9.
10.
11.
Схеми розв’язання основних типів рівнянь з модулем:
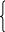
f
(x) = g (x),
x
,
1
.
f
f (-x) = g (x),
x <0;
f (x) = g (x),
f
(x)
0
g (x)
,
2
.
f (x)= g (x),
-f (x) = g (x), f (x) = -g (x);
f (x) < 0
f (x) = g (x),
3.
f
(x)
= g
(x)
f (x) = -g(x)
4.
5.
6.
7.
8.
9.
10.
,
де
f
(x),
i
=
,
g(x)
– деякі функції.
Часто
розв’язування таких рівнянь послідовним
розкриттям знаків модуля дуже громіздке.
Такі рівняння найпростіше розв’язувати
методом
інтервалів.
Для цього знаходять всі точки, в яких
хоча б одна із функцій f
(x),
i=
змінює знак. Ці точки ділять область
допустимих значень рівняння на проміжки,
на кожному з яких всі функції f
(x),
і
=
зберігають
знак. Використовуючи означення модуля,
переходять від рівняння до сукупності
систем, які не містять знаків модулів.
Аналогічно можна розв’язувати і відповідні нерівності:
.
§ 2. Рівняння.
Для розв’язання рівняння, що містить модулі, у загальному випадку потрібно розглянути це рівняння на всіх проміжках, на яких вирази під знаками модулів не змінюють знак, розкрити модулі і розв’язати відповідні рівняння на кожному з проміжків.
Приклад 1.
Розв’язати рівняння:
.
Розв’язання
Функції під знаками модуля дорівнюють нулю відповідно в точках х=-1 і х=0. Ці точки розбивають числову вісь на три проміжки. На кожному з цих проміжків обидві функції під знаками модуля зберігають знаки, і тому, враховуючи означення модуля, утворимо рівносильну сукупність мішаних систем:
або
або
Звідки отримуємо розв’язок, що випливає з першої системи.
Відповідь:
.
Приклад 2.
Розв’язати
рівняння :
.
Розв’язання
Функція під першим знаком модуля має корені х=1, х=2, а дискримінант другого квадратного тричлена від’ємний, тому даному рівнянню відповідає така система:
якщо
Розв’язавши яку, отримаємо рівносильну сукупність мішаних систем:
або
Перша і друга системи не мають розв’язків.
Відповідь: не моє розв’язків.
Приклад 3.
Розв’язати рівняння:
Розв’язання
Розкриємо спочатку зовнішній модуль, а потім внутрішній, користуючись означенням модуля.
Відповідь:
Приклад 4.
Розв’язати рівняння:
Розв’язання
Під час розв’язання даного рівняння використаємо означення модуля, та після перетворень отримаємо:
1)
2)
дана система не має розв’язків.
Відповідь: 3.
Приклад 5.
Розв’язати рівняння:
Розв’язання
Розкриваючи модуль, отримаємо сукупність двох систем:
1)
Другий розв’язок рівняння не задовольняє систему.
2)
Відповідь:
Приклад 6.
Розв’язати рівняння:
Розв’язання
1)
2)
3)
Відповідь: жодна із систем не має розв’язків.
Приклад 7.
Розв’язати рівняння:
Розв’язання
У цьому рівнянні користуватись методом інтервалів не доцільно, а слід згадати, що два модулі будуть рівними, якщо вирази під знаками модулів або рівні, або протилежні. Тому маємо рівносильну сукупність рівнянь:
З якої знаходимо результат.
Відповідь:
Приклад 8.
Розв’язати рівняння:
Розв’язання
Використовуючи властивість рівності модулів, отримаємо рівносильне рівняння даному:
Розв’язавши дану систему отримаємо
Відповідь:
Рівняння для самостійного розв’язання:
1.
7.
2.
8.
3.
9.
4.
10.
5.
;
6.