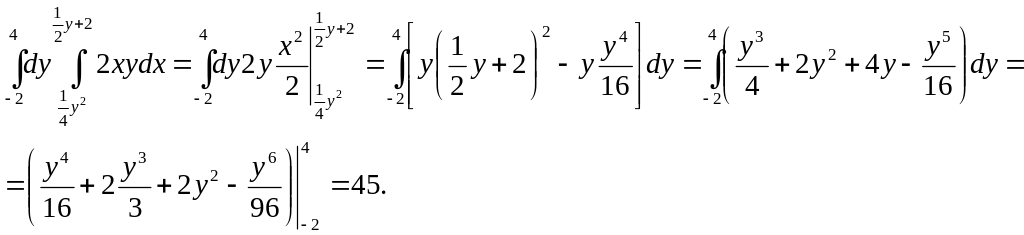- •Для экономистов
- •Часть III
- •Лукинова с. Г.
- •Для экономистов
- •Часть III
- •Содержание.
- •Интегральное исчисление
- •Дифференциальные уравнения
- •Приложения в экономике
- •1. Программа, цели и задачи дисциплины, сфера профессионального использования
- •2 Теоретическая часть
- •2.1 Интегральное исчисление
- •2.1.1 Неопределённый интеграл, его свойства
- •Интегралы от основных элементарных функций (Таблица интегралов)
- •2.1.2 Методы интегрирования
- •2.1.3 Определённый интеграл, его свойства
- •2.1.4 Теорема Ньютона-Лейбница
- •Интегрирование по частям
- •2.1.5 Геометрические приложения определённого интеграла Вычисления площадей плоских фигур
- •2.1.6 Несобственные интегралы
- •Пример 13 Исследовать на сходимость интегралы:
- •Пример 14
- •2.1.7 Понятие двойного интеграла
- •2.2 Дифференциальные уравнения
- •2.2.1 Основные понятия. Дифференциальные уравнения первого порядка. Задача Коши.
- •2.2.2 Простейшие типы дифференциальных уравнений первого порядка.
- •Линейные дифференциальные уравнения
- •Уравнением Бернулли
- •2.2.3 Дифференциальные уравнения второго порядка, допускающие понижение порядка.
- •Линейные дифференциальные уравнения высших порядков
- •2.2.5 Линейные однородные дифференциальные уравнения с постоянными коэффициентами.
- •2.2.6 Линейные неоднородные дифференциальные уравнения. . Метод Лагранжа
- •2.2.7 Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами и специальной правой частью
- •2.3 Ряды
- •Числовые ряды. Основные понятия. Необходимый признак сходимости ряда
- •Свойства сходящихся числовых рядов
- •2.3.2 Достаточные признаки сходимости рядов
- •2.3.3 Знакопеременные ряды. Признак Лейбница
- •Пример 37 Исследовать ряд на сходимость.
- •2.3.4 Функциональные ряды. Степенные ряды
- •Разложение функций в степенные ряды. Ряды Тейлора, Маклорена
- •Применение рядов в приближенных вычислениях
- •2.4 Приложения в экономике
- •2.4.1 Приложения интегрального исчисления в экономике
- •2.4.2 Приложения дифференциальных уравнений в экономике.
- •Это дифференциальное уравнение – с разделяющимися переменными. Решим его:
- •3. Руководство к изучению разделов Тема: Неопределенный интеграл
- •Тема: Определенный Интеграл
- •Тема: Дифференциальные уравнения
- •Тема: Ряды
- •4. Вопросы и задания для самооценки
- •Понятие двойного интеграла.
- •6. Вопросы к экзамену
- •Неопределённый интеграл, его свойства
- •Теорема Ньютона-Лейбница
- •Дифференциальные уравнения второго порядка, допускающие понижение порядка
- •Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами и специальной правой частью
- •Применение рядов в приближенных вычислениях
- •7 Конспект-схемы
- •Разложение многочлена на линейные и квадратные множители
- •(Таблица интегралов)
- •Кс 4. Интегрирование тригонометрических выражений.
- •1) При вычислении
- •2) При вычислении ,
- •4) При вычислении
- •Приложение а Контрольная работа №3 «Интегральное исчисление. Применение в экономике.»
- •Задачи 141 – 160 Исследовать на сходимость числовой ряд:
- •Варианты контрольных работ
- •Приложение с Алфавитно-предметный указатель (ключевые слова)
- •Литература
2.1.6 Несобственные интегралы
При введении понятия определённого интеграла мы предполагали, что подынтегральная функция является ограниченной, а пределы интегрирования – конечными. Такой интеграл называется собственным (слово «собственный» обычно опускается). Если хотя бы одно из этих двух условий не выполнено, то интеграл называется несобственным.
Интегралы с бесконечными пределами интегрирования
Пусть функция f(x)
непрерывна при
![]() <
<![]() ,
т.е. при
,
т.е. при
![]() Тогда по определению полагают
Тогда по определению полагают
![]()
Если этот предел существует, то говорят, что интеграл
![]()
сходится, а если предел не существует, то интеграл называют расходящимся.
Геометрически для
неотрицательной при
![]() функции f(x)
несобственный интеграл по аналогии с
собственным интегралом представляет
собой площадь фигуры, ограниченной
сверху графиком функции y=f(x),
слева отрезком прямой x=a
и снизу осью Ox.
функции f(x)
несобственный интеграл по аналогии с
собственным интегралом представляет
собой площадь фигуры, ограниченной
сверху графиком функции y=f(x),
слева отрезком прямой x=a
и снизу осью Ox.

Пример 13 Исследовать на сходимость интегралы:
а)
![]() т.е. данный несобственный интеграл
сходится.
т.е. данный несобственный интеграл
сходится.
б)
![]() т.е. данный интеграл расходится.
т.е. данный интеграл расходится.
в) Установим, при
каких значениях
![]() интеграл
интеграл
![]() сходится.
сходится.
Случай
![]() был рассмотрен в примере б). Если
был рассмотрен в примере б). Если
![]() то
то
![]() .
.
Значит, данный
интеграл сходится при
>1
и расходится при
![]()
Аналогично определяются следующие несобственные интегралы
![]()
![]()
![]()
Интегралы от неограниченных функций
Пусть функция f(x)
непрерывна при
<b.
Пусть эта функция стремится к бесконечности,
когда
![]() (т.е. на отрезке
функция f(x)
не ограничена). Положим
(т.е. на отрезке
функция f(x)
не ограничена). Положим
![]()
Если этот предел существует, то говорят, что интеграл
![]()
сходится, а если предел не существует, то интеграл называют расходящимся.
Подобным же образом равенство
![]()
даёт определение
интеграла от функции f(x), стремящейся к
бесконечности при
![]()
Наконец, если
функция f(x) стремится к бесконечности
при приближении аргумента к обоим концам
промежутка
![]() ,
то полагают
,
то полагают
a<c<b.
Если при этом сходятся оба интеграла в правой части последнего равенства, то сходится и интеграл слева.
Пример 14
![]() ,
т.е. расходится.
,
т.е. расходится.
2.1.7 Понятие двойного интеграла
Рассмотрим функцию
двух переменных z=f(x,y)
или z=f(M),
определённую и непрерывную в замкнутой
ограниченной области D
плоскости Oxy;
![]() .
.
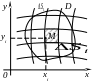
Разобьем область
D
произвольным образом на элементарные
участки
![]() , площади которых также обозначим
, площади которых также обозначим
![]() , а диаметры
обозначим d.
Выберем произвольно точку
, а диаметры
обозначим d.
Выберем произвольно точку
![]() .
.
Интегральной суммой для функции по области называется:
![]() .
.
Если существует
предел последовательности интегральных
сумм
![]() при
при
![]() ,
то он называется двойным интегралом от
функции f(M)
по области D,
обозначают:
,
то он называется двойным интегралом от
функции f(M)
по области D,
обозначают:
![]()
Замечание:
Предел не зависит ни от способа разбиения области на элементарные участки , ни от выбора точек .
Вычисление двойного интеграла сводится к вычислению повторных интегралов следующим образом.
Для непрерывной
функции
![]() двойной интеграл по области
двойной интеграл по области
![]() равен повторному интегралу:
равен повторному интегралу:
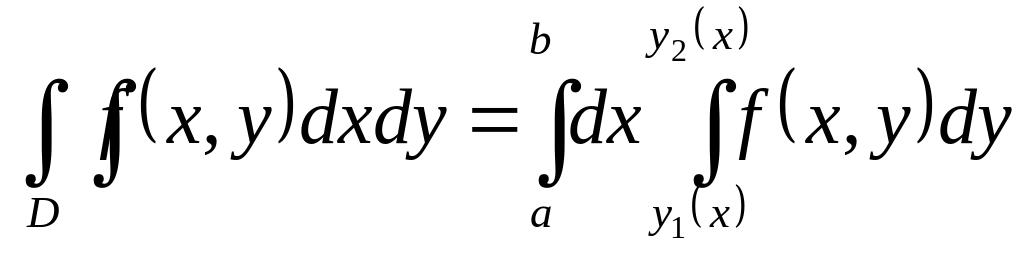 (1)
(1)
или
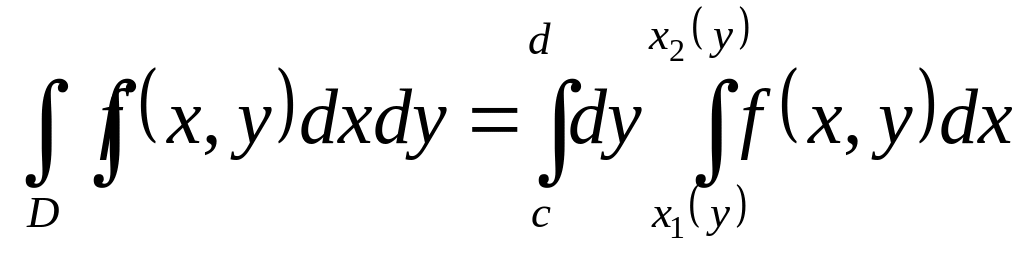 (2)
(2)
Повторные интегралы
(1) и (2) отличаются друг от друга порядком
интегрирования по переменным
![]() и
и
![]() .
Применение формулы (1) или (2) зависит от
конфигурации области
.
Формула (1) применяется в тех случаях,
когда область
ограничена снизу и сверху соответственно
кривыми
.
Применение формулы (1) или (2) зависит от
конфигурации области
.
Формула (1) применяется в тех случаях,
когда область
ограничена снизу и сверху соответственно
кривыми
![]() и
и
![]() ,
а слева и справа прямыми
,
а слева и справа прямыми
![]() ,
причем всюду на
,
причем всюду на
![]() функции
и
непрерывны
и
функции
и
непрерывны
и
![]() .
Примеры таких областей приведены на
рисунке.
.
Примеры таких областей приведены на
рисунке.
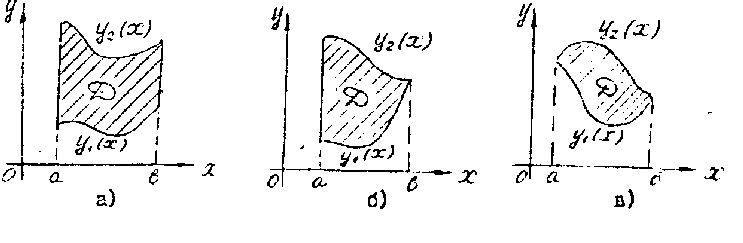
Формулу (2) применяют
в тех случаях, когда область
ограничена слева и справа соответственно
кривыми
![]() и
и
![]() .
Снизу и сверху - прямыми
.
Снизу и сверху - прямыми
![]() .
Причем всюду на
.
Причем всюду на
![]() функции
функции
![]() непрерывны
непрерывны
![]() .
На рисунке изображены примеры таких
областей.
.
На рисунке изображены примеры таких
областей.

Вычисление двойного
интеграла в декартовой системе координат
сводится к последовательному вычислению
двух определенных интегралов по формулам
(1) или
(2). При
применении формулы (1) сначала вычисляют
внутренний интеграл
 при постоянном
,
полученная функция от
интегрируется в пределах от
при постоянном
,
полученная функция от
интегрируется в пределах от
![]() до
до
![]() .
.
Если применяют
формулу (2), то сначала вычисляют
внутренний интеграл
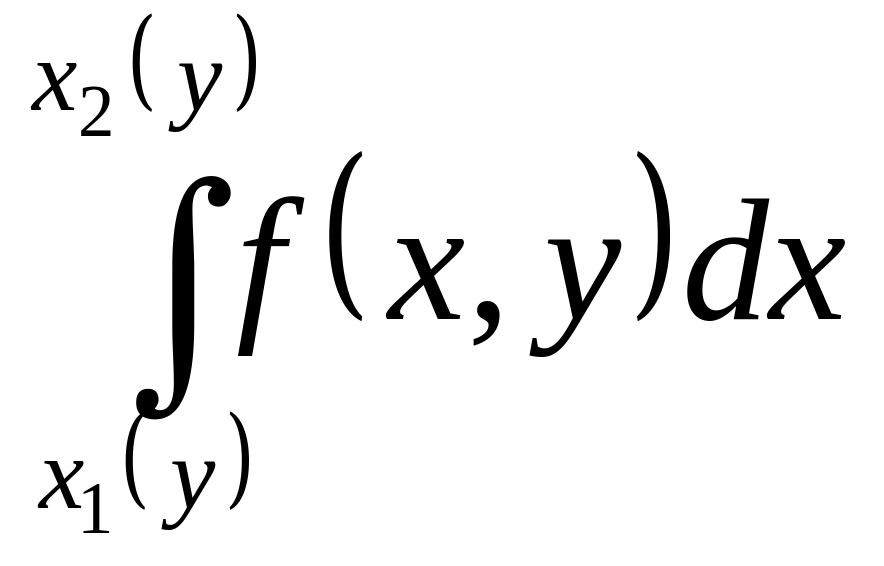 при постоянном
;
затем полученная функция от
интегрируется на отрезке
.
при постоянном
;
затем полученная функция от
интегрируется на отрезке
.
Покажем, как вычисляется двойной интеграл в декартовой системе координат.
Пример
15 Вычислить
![]() где область
ограничена линиями
где область
ограничена линиями
![]() .
.
Решение:
Построим область
:
уравнение
![]() является уравнением параболы, симметричной
относительно оси
является уравнением параболы, симметричной
относительно оси
![]() ,
с вершиной в начале координат. Уравнение
,
с вершиной в начале координат. Уравнение
![]() есть уравнение прямой.
есть уравнение прямой.
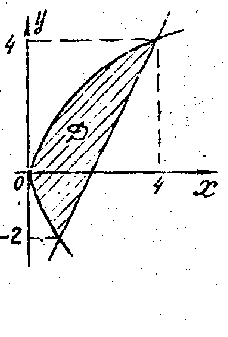
Найдем координаты точек пересечения параболы и прямой, для этого решим систему уравнений:
![]()
Решая второе
уравнение, найдем
![]() - ординаты точек пересечения параболы
и прямой. Таким образом, область
ограничена слева параболой:
- ординаты точек пересечения параболы
и прямой. Таким образом, область
ограничена слева параболой:
![]() ,
справа прямой
,
справа прямой
![]() ,
снизу н сверху соответственно прямыми
,
снизу н сверху соответственно прямыми
![]() и
и
![]() .
Применяя формулу (2), запишем исходный
двойной интеграл в виде
.
Применяя формулу (2), запишем исходный
двойной интеграл в виде
 ,
,
Вычисляя сначала внутренний интеграл по dx , затем внешний, получим: