Понятие первообразной функции. Теоремы о первообразных
Неопределённый интеграл, его свойства
Основные правила и формулы интегрирования
Метод замена переменной (подстановки)
Интегрирование по частям в неопределённом интеграле
Разложение рациональной функции на простейшие дроби
Интегрирование простейших дробей
Интегрирование рациональных функций
Интегрирование выражений, содержащих тригонометрические функции
Интегрирование иррациональных выражений
Понятие определённого интеграла, его геометрический смысл
Основные свойства определённого интеграла
Теорема об оценке интеграла
Теорема о среднем
Теорема Ньютона-Лейбница
Замена переменной и интегрирование по частям в определённом интеграле
Вычисление площадей плоских фигур
Вычисление объемов тел вращения
Двойной интеграл, его вычисление
Применение интегрального исчисления в экономике
Основные понятия теории дифференциальных уравнений. Задача Коши для дифференциального уравнения первого порядка. Формулировка теоремы существования и единственности решения задачи Коши.
Дифференциальные уравнения первого порядка с разделяющимися переменными
Однородные дифференциальные уравнения первого порядка
Линейные уравнения первого порядка
Уравнение Бернулли
Дифференциальные уравнения высших порядков. Задача Коши. Формулировка теоремы существования и единственности решения задачи Коши. Общее и частное решения.
Дифференциальные уравнения второго порядка, допускающие понижение порядка
Линейный дифференциальный оператор, его свойства
Линейное однородное дифференциальное уравнение, свойства его решений
Линейно-зависимые и линейно-независимые системы функций. Необходимое условие линейной зависимости системы функций
Линейное однородное дифференциальное уравнение. Фундаментальная система решений. Структура общего решения
Линейное неоднородное дифференциальное уравнение. Структура общего решения
Метод Лагранжа вариации произвольных постоянных
Линейные однородные дифференциальные уравнения с постоянными коэффициентами (случай простых корней характеристического уравнения)
Линейные однородные дифференциальные уравнения с постоянными коэффициентами (случай кратных корней характеристического уравнения)
Линейные однородные дифференциальные уравнения с постоянными коэффициентами (случай комплексно-сопряженных корней характеристического уравнения)
Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами. Метод Лагранжа
Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами и специальной правой частью
Применение дифференциальных уравнений в экономике
Числовой ряд. Сходимость и сумма ряда
Необходимый признак сходимости ряда
Достаточный признак сходимости ряда. Признак сравнения
Признаки Д’Аламбера и Коши
Интегральный признак сходимости ряда
Теорема Лейбница. Оценка остатка знакочередующегося ряда
Теорема о сходимости абсолютно сходящегося ряда. Свойства абсолютно сходящихся рядов
Теорема Абеля. Интервал и радиус сходимости степенного ряда
Разложение функции в степенной ряд. Ряд Тейлора
Разложение функции в степенной ряд. Ряд Маклорена
Разложение по степеням функций
Разложение по степеням функций
Разложение по степеням функций
Применение рядов в приближенных вычислениях
7 Конспект-схемы
КС 1. Разложение многочленов на множители.
многочлен n-ой степени
Теорема Безу:
, где z0 простой корень
, где z0 корень кратности k
Если z0 корень комплексный, , где i=
и ,
то , где – сопряженный корень.
Разложение многочлена на линейные и квадратные множители
– действительные
корни;
комплексные корни
КС 2. Интегралы от основных элементарных функций.
(Таблица интегралов)
.
, в общем случае
, в частности
9)
10)
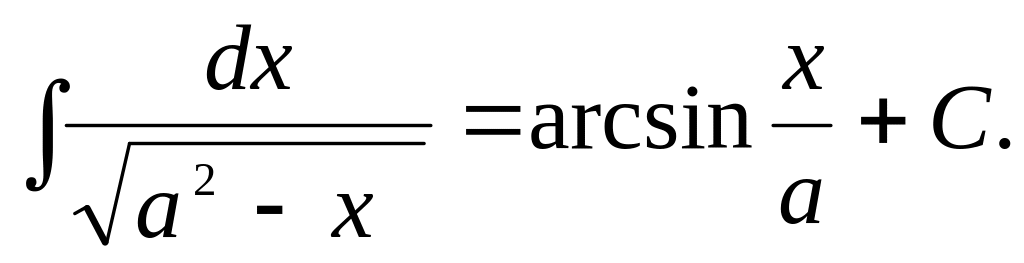
11)
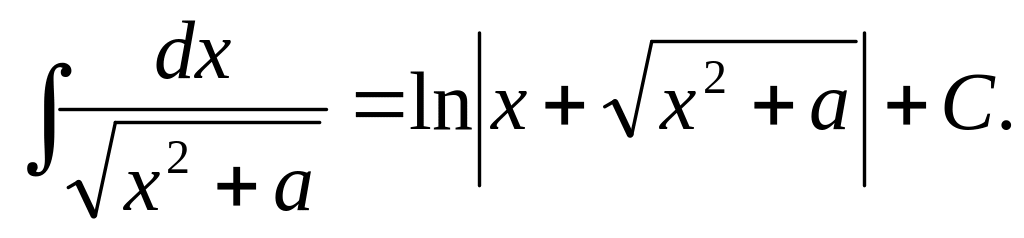
12)
КС 3. Интегрирование рациональных дробей.
Рациональная дробь или рациональная функция – отношение двух многочленов.
, если ,
где
Простейшие типы рациональных дробей:
I) ; III) ;
II) ; IV)
Разложение правильной рациональной дроби на сумму простейших дробей:
Интегралы от простейших рациональных дробей:
I) ;
II) ;
III)
IV)
Интегралы III и IV типов вычисляют заменой .
Кс 4. Интегрирование тригонометрических выражений.
1) При вычислении
a) n – нечётное
b) n, m – чётные, .
применяют формулы:
2) При вычислении ,
применяют формулу:
Например,
а)
б)
или делают замену:
, тогда
3)
Универсальная тригонометрическая
подстановка
, тогда 
; 
; 
.
4) При вычислении
используют формулы
КС 5. Интегрирование иррациональных выражений
1)
,
2)
,
КС 6. Определённый интеграл.
ф
ормула
Ньютона-Лейбница:
Вычисление площади:
Криволинейной
трапеции
П
роизвольной
фигуры
2. Вычисление объёмов тел вращения:
y
В
ращение
вокруг оси x
абсцисс
Вращение вокруг
оси ординат
КС 7. Дифференциальные уравнения 1-го порядка.
общее
решение:
Задача Коши:
Найти частное решение ,
удовлетворяющее
начальным условиям
Простейшие типы дифференциальные уравнения 1-го порядка:
1)
,
решение
2)
с разделяющимися
переменными
,
решение
3)
однородное
,
замена
,
4)
линейное
,
замена
,
КС 8. Дифференциальные уравнения 2-го порядка.
общее
решение:
Задача Коши:
Найти
частное решение
,
удовлетворяющее начальным условиям
Дифференциальные уравнения 2-го порядка, допускающие понижение порядка:
1)
,
решение
,
2)
,
замена
,
3)
,
замена
,
КС 9. Дифференциальные уравнения 2-го порядка.
Линейные, однородные с постоянными коэффициентами.
,
– характеристическое
уравнение.
– дискриминант.
В зависимости от знака D:
1)
– действительные числа:
общее
решение
2)
– действительные числа:
общее
решение
3)
– комплексные числа:
общее
решение
/
КС 10. Дифференциальные уравнения 2-го порядка.
Линейные неоднородные с постоянными коэффициентами.
,
общее решение: ,
где – общее решение однородного дифф.ур. (см. КС 8)
– частное решение, вид функции зависит от вида правой части дифференциального уравнения :
Вид |
Вид |
|
, если , если , если |
|
|
в частности или |
, если , если , если , если |
|
|
,
если
,
если
,
если
где
;
если