1.2. Компенсація реактивної потужності

Будь-який промисловий споживач електроенергії, як навантаження енергетичної мережі, має комплексний характер і, в загальному випадку, може бути нелінійним. Однак, в даній роботі ми обмежимось розглядом лише лінійних комплексних навантажень, які частіше мають індуктивний характер.

Як відомо з дисципліни «Основи теорії електронних кіл» [1] будь-яке комплексне навантаження може бути представлене за допомогою послідовної, або паралельної схем заміщення. У даному випадку зручнішою є паралельна схема заміщення при якій навантаження можна представити як комплексну провідність і представити на комплексній площині провідностей (рис. 4). Нагадаємо, що реактивна провідність індуктивності визначається за формулою і є від’ємною величиною.

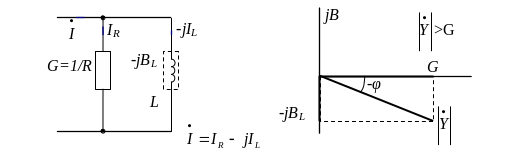
Рис. 4. Схема заміщення комплексного навантаження та його векторна діаграма

При цьому загальний струм, який протікає через навантаження є комплексною величиною . Його амплітудне значення дорівнює .

Якщо тепер паралельно до навантаження додатково підключити конденсатор з ємністю, яка б забезпечувала провідність +jB_C з виконанням умови

, (15)

то сума струмів через індуктивну і ємнісну складові навантаження стане рівною нулю, що забезпечить повну компенсацію реактивної складової навантаження, як показано на рис. 5. У результаті, повний струм навантаження стане рівний струму його активної складової .

Рис. 5. Схема компенсація індуктивної складової навантаження паралельним увімкненням конденсатора та його векторна діаграма

Як видно з векторної діаграми, при повній компенсації кут φ=0, а коефіцієнт потужності (13) . При цьому реактивна потужність Q дорівнює нулю, а повна потужність дорівнює активній S=P.

Інакше компенсацію реактивної складової ще можна прояснити як забезпечення умови резонансу в паралельному коливальному контурі LC. Як відомо, опір реального паралельного коливального контура на резонансі є значно більшим за активну складову опору навантаження і тому його впливом можна знехтувати.

На практиці не ставлять за мету досягти повної компенсації реактивної потужності, оскільки окрім чисто технічних чинників важливу роль відіграють економічні. Вони пов’язані з угодами на постачання електроенергії та на закупівлю і обслуговування компенсуючих пристроїв. Як правило достатньо підтримувати коефіцієнт потужності в межах 0,93

Таким чином, при підключенні паралельно до навантаження компенсуючих конденсаторів виникає реактивна потужність Q_C, яка компенсує частину реактивної потужності навантаження Q (див. рис. 6). За рахунок такої компенсації повна потужність знижується до величини S_К, а коефіцієнт потужності після компенсації – зростає.

Рис. 6. Трикутник потужностей після компенсації частини реактивної потужності

Для контролю різниці фаз між струмом і напругою до (φ) і після (φ_к) компенсації, в даній лабораторній роботі використано двоканальний осцилограф (див. рис.2. і формулу (7)). Осцилограму струму отримуємо за допомогою додаткового допоміжного опору R_S, який увімкнено послідовно з навантаженням (див. рис. 7) при виконані умові, що величина цього опору значно менша за модуль опору навантаження. В такому випадку можна вважати, що струм, який протікає у колі, пропорційний спаду напруги на цьому опорі. У результаті на екрані осцилографа отримаємо залежності, подібні до тих, що показано на рис. 2. Це дозволить визначити усі параметри напруги і струму комплексного навантаження і записати їх миттєві значення (див. формули (7) і (8)).