МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ “ЛЬВІВСЬКА ПОЛІТЕХНІКА”

Дослідження енергетичних параметрів лінійного комплексного навантаження методичні вказівки

до лабораторної роботи з дисциплін

“Електротехнічні пристрої РЕЗ”

для студентів базового напряму 6.050901 „Радіотехніка”

та “Електроживлення комплексів зв’язку”

для студентів базового напряму 6.050903 „Телекомунікації”

Затверджено на засіданні кафедри радіоелектронних пристроїв та систем.

Протокол № 12 від 05.04.2012

Реєстраційний № 4191

від 31 травня 2012 р

Львів – 2012

Дослідження енергетичних параметрів лінійного комплексного навантаження: Методичні вказівки до лабораторної роботи з дисциплін “Електротехнічні пристрої РЕЗ” для студентів напряму 6.050901 „Радіотехніка” та “Електроживлення комплексів зв’язку” для студентів напряму 6.050903 „Телекомунікації” /Укл.: В.Г. Сторож – Львів: Видавництво Національного університету „Львівська політехніка”, 2012.–  16 с.

Укладач Сторож В.Г. , канд. техн. наук., доцент

Відповідальний за випуск І.Н. Прудиус, д-р. техн. наук, професор

Рецензенти М.М. Климаш, д-р. техн. наук, професор

Мета роботи – навчитися визначати енергетичні параметри лінійного комплексного навантаження та ознайомитись з методами компенсації реактивної потужності.

1. Теоретична частина

Електроенергія надходить до споживача у вигляді гармонічної напруги (рис .1.). Тому спочатку дамо визначення основним параметрам такої напруги: амплітуді, періоду, частоті, початковій фазі, діючому значенню напруги, середньому значенню напруги, миттєвій потужності, середній потужності.

Графічне представлення гармонічної напруги показано на рис. 1.

Рис. 1. Представлення гармонічної напруги у вигляді залежності її миттєвого значення від часу

Амплітуда U_m – це максимальна велична відхилення змінної періодичної напруги від її середнього значення. В даному випадку від нуля;

Період Т – це часовий проміжок, за який стан коливання повторюється (при цьому фаза коливання змінюється на 2π, або 360º);

Частота коливань f=1/Т – показує скільки коливань здійснюється за одну секунду;

Колова (циклічна) частота ω=2πf=2π/Т – показує на яку величину змінюється фаза коливання за одну секунду (це швидкість зміни фази коливання);

Фаза коливання (ωt + φ₀) – визначає стан коливання в даний момент часу, де φ₀ – початкова фаза, яка визначає стан коливання відносно початку відліку в прийнятій системі координат (наприклад, при t=0);

У результаті, аналітичний вираз, який описує миттєве значення напруги (рис. 1), може бути представлений за допомогою функції синус

, (1)

або функції косинус

, (2)

де .

Знак плюс перед значенням початкової фази у виразі (1) означає випередження коливання відносно початку координат, а знак мінус у виразі (2) – запізнення. Для зручності, замість змінної часу t часто використовують змінну ωt. В такому випадку, незалежно від робочої частоти, період повторення коливань завжди буде дорівнювати 2π, а відповідні вирази матимуть наступний вигляд:

, (3)

або

. (4)

Середнє значення (постійну складову) періодичної напруги довільної форми визначають за наступними виразами:

або . (5)

Постійна складова гармонічної напруги (рис. 1) дорівнює нулю.

Діюче (ефективне, середньоквадратичне) значення змінної періодичної напруги – це еквівалентна їй постійна напруга, яка будучи прикладена до того самого активного опору навантаження забезпечить виділення в ньому такої самої кількості потужності, що й дана змінна напруга. В іноземній літературі діючу напругу позначають U_rms (rms – root-mean-square).

Якщо відома функція, яка описує миттєве значення періодичної напруги, то її діюче значення можна розрахувати за допомогою наступних виразів:

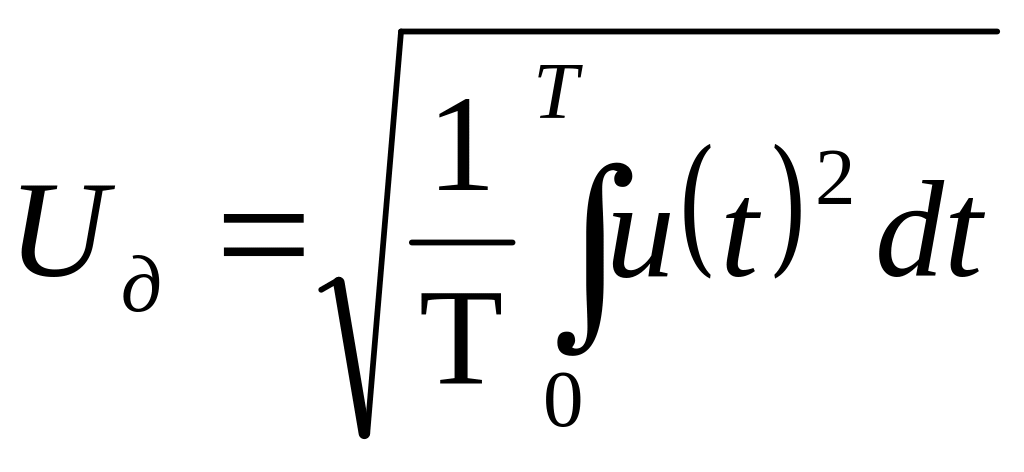, або . (6)

Зокрема для гармонічної напруги з амплітудою U_m діюче значення напруги . Коефіцієнт пропорційності між діючим і амплітудним значеннями змінної періодичної напруги залежить від форми змінної напруги. Наприклад, діюче значення змінної періодичної напруги у вигляді меандру дорівнює її амплітудному, а для змінної напруги трикутної форми .

Якщо гармонічну напругу прикласти до лінійного комплексного навантаження Z_H то через нього почне протікати гармонічний струм. Усі параметри гармонічного струму можна визначити на основі виразів (1) – (6) здійснивши заміни ; ; ; і врахувавши початкову фазу струму.

В загальному випадку гармонічні напруга і струм при лінійному комплексному навантаженні будуть мати вигляд, як показано на рис. 2.

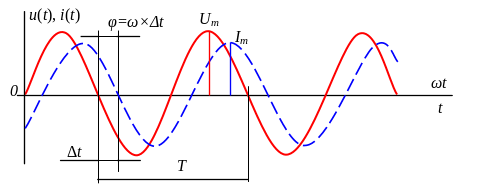
Рис. 2. Форма напруги та струму при лінійному комплексному навантаженні

Таку залежність можна отримати, наприклад, за допомогою двоканального осцилографа і відразу визначити різницю в часі між цими двома коливаннями Δt (див. рис. 2). Тоді різниця фаз між ними дорівнює:

, (7)

Таким чином φ – це різниця фаз між струмом і напругою. Визначивши амплітуди, період і різницю фаз можна записати аналітичні вирази для миттєвих значень напруги і струму. Наприклад, для випадку, що показаний на рис. 2:

та . (8)

Знак мінус перед φ означає, що струм по фазі затримується відносно напруги, що має місце при комплексному навантаженні, яке має індуктивний характер. Якщо навантаження має ємнісний характер, то перед φ ставиться знак плюс. При активному навантаженні φ=0.

Наявність струму, що протікає через навантаження при прикладеній до нього напрузі, свідчить про те, що навантаження споживає потужність. Якщо лінійне комплексне навантаження живиться від джерела гармонічної напруги, що має місце в даній лабораторній роботі, то розглядають наступні види потужності: миттєву потужність; повну потужність; активну потужність; реактивну потужність.

Миттєва потужність визначає, яку потужність споживає навантаження в даний момент часу:

. (9)

Для лінійного комплексного навантаження миттєва потужність не є постійною величиною і за один період коливання може приймати як додатні так і від’ємні значення. Якщо миттєва потужність більше нуля, то це означає, що в даний момент часу навантаження споживає електроенергію від мережі електроживлення, якщо менше нуля – то віддає її назад у мережу.

Повна потужність визначається як добуток діючого значення напруги на діюче значення струму:

. (10)

Повна потужність вимірюється у вольт-амперах (ВА).

Активна потужність для періодичних напруги і струму будь-якої форми визначається шляхом усереднення споживаної енергії за один період коливання:

, або . (11)

Активна потужність вимірюється у ватах (Вт) і завжди є додатною величиною. Вона визначає швидкість споживання електроенергії, а саме, перетворення електричної енергії мережі електроживлення в інші види енергії: механічну в електродвигунах, теплову в електронагрівачах, випромінювану енергію НВЧ сигналу на радіопередавальних центрах та ін. При цьому кількість новоствореної енергії залежить також від коефіцієнта корисної дії відповідного устаткування.

У випадку гармонічної напруги і струму, що має місце в даній лабораторній роботі, активну потужність можна визначити за допомогою виразу:

. (12)

Нагадаємо, що φ – це різниця фаз між струмом і напругою. Відношення має назву коефіцієнта потужності, який надалі позначатимемо . Для лінійного комплексного навантаження коефіцієнт потужності

. (13)

Реактивна потужність визначається за наступним виразом:

. (14)

Реактивна потужність вимірюється у вольт-амперах реактивних (ВАр).

Як було сказано вище, корисну роботу виконує лише активна потужність Р. Реактивна потужність Q затрачається на перезаряджання реактивної складової комплексного опору навантаження. Двічі за період одного коливання ця реактивність заряджається і двічі розряджається. Цей процес ще називають перетіканням реактивної енергії між джерелом напруги і навантаженням.

Усі складові потужності лінійного комплексного навантаження зручно представити графічно у вигляді, так званого трикутника потужностей, який показано на рис. 3. При цьому повну потужність записують як комплексну величину так: , або її модуль .

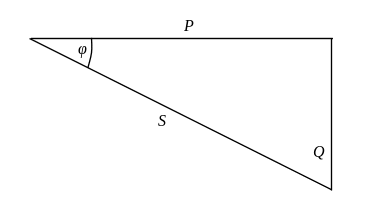
Рис. 3. Трикутник потужностей

У результаті, якщо для виконання корисної роботи необхідно затратити активну потужність P, то, за рахунок наявності реактивної потужності Q, джерело електроенергії повинно віддавати в мережу більшу потужність – повну потужність S. Це призводить до зростання активних непродуктивних втрат в колах енергетичної мережі (проводи, трансформатори, комутаційні пристрої).

Для підвищення якості електроенергії та зменшення активних непродуктивних втрат необхідно, щоби коефіцієнт потужності був близький до одиниці. В енергетичних мережах це забезпечується введенням компенсуючих (косинусних) конденсаторів, або реакторів відповідного номіналу.