Критерий Колмогорова

Кроме критерия Пирсона, для оценки степени согласованности теоретического и эмпирического(статистического) распределений на практике применяется еще и ряд других критериев. Рассмотрим кратко критерий Колмогорова.

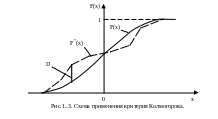
В качестве меры расхождения между теоретическим и статистическим распределениями А.Н. Колмогоров рассматривает максимальное значение модуля разности между статистической функцией распределения F^*(x) и выбранной теоретической функцией распределения F(x) (рис.1.3):

Основанием для выбора в качестве меры расхождения величины D является простота ее вычисления и достаточно простой закон распределения. Колмогоров доказал, что какова бы ни была функция распределения F(x) непрерывной СВ Х, при неограниченном возрастании числа независимых наблюдений n вероятность неравенства

стремится к пределу

Значения вероятности , подсчитанные по этой формуле, приведены в таблице 1.3.

Таблица 1.3

Значения критерия Колмогорова

0,0 0,1 0,2 0,3 0,4 0,5 0,6	1,000 1,000 1,000 1,000 0,997 0,964 0,864	0,7 0,8 0,9 1,0 1,1 1,2 1,3	0,711 0,544 0,393 0,270 0,178 0,112 0,068	1,4 1,5 1,6 1,7 1,8 1,9 2,0	0,040 0,022 0,012 0,006 0,003 0,002 0,001

Схема применения критерия Колмогорова следующая:

1. Строятся статистическая функция распределения F^*(x) и предполагаемая теоретическая функция распределения F(x) (рис.1.3). Для их построения составляется таблица с результатами расчетов этих функций по форме табл. 1.4.

Функции рассчитываются для нижних границ интервалов, полученных при построении статистического ряда (табл.1.1), используемого затем для построения гистограммы. Оттуда же берутся и вероятности F^*(x), равные соответствующим частотам . Значения теоретической функции распределения F(x) рассчитываются по функции, описывающей выбранное для сравнения распределение СВ Х.

При выборе нормальной функции распределения ее значения определяются с использованием функции Лапласа , значения которой табулированы и приведены в табл. П.1.3. Порядок использования этой таблицы аналогичен порядку, применяемому при расчете критерия Пирсона.

Таблица 1.4

Результаты расчета статистической f*(X) и теоретической f(X) функций распределения

Значение кон­тролируемого параметра			…		…
Значение ста­тистической функции рас­пределения F*(x)			…		…
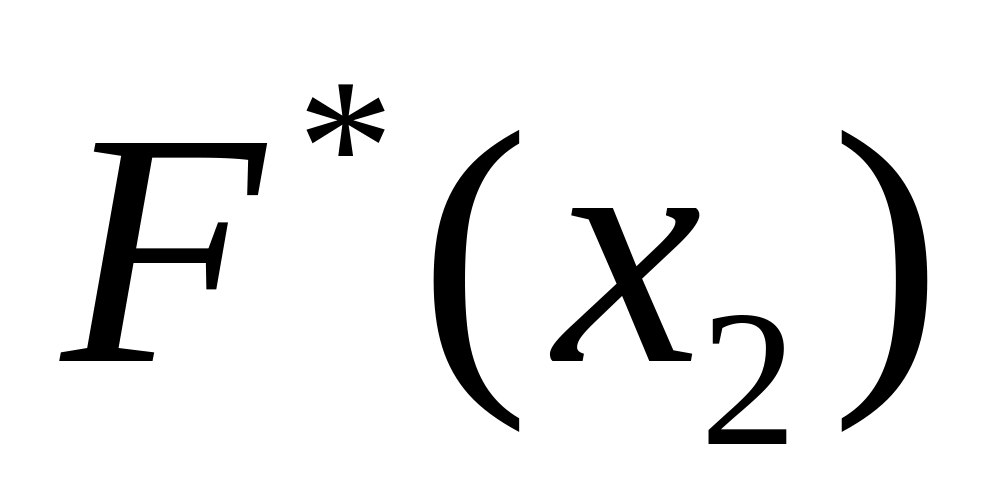
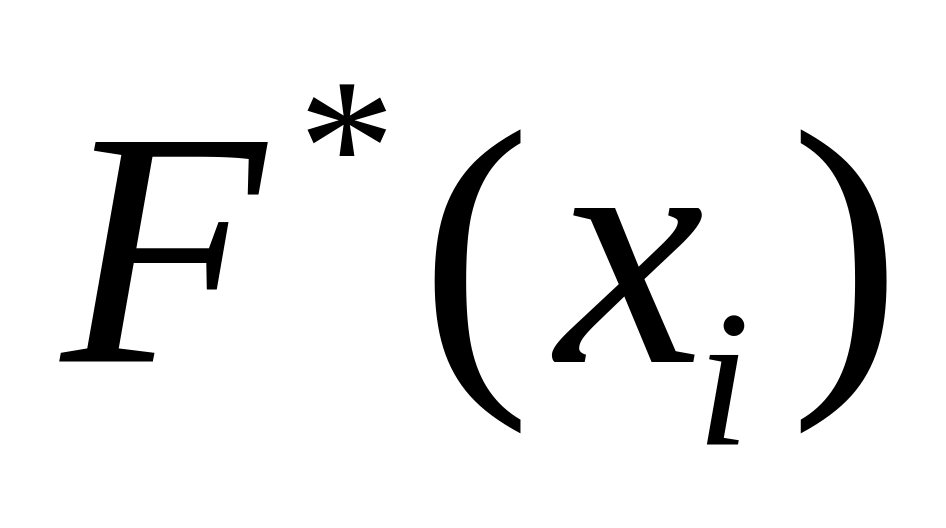
Значение тео­ретической функции рас­пределения F(x)			…		…

2. Определяется максимум D модуля разности между функциями F^*(x) и F(x) (рис. 1.3).

3. Определяется величина

.

4. По табл.1.3 при выбранной вероятности (обычно выбирается, как и ранее, близкой к 0,9 или 0,95) определяется критическое значение .

5. Сравниваются значения и . Если при этом

< то гипотеза о соответствии выбранной теоретической функции распределения F(x) и статистической F^*(x) с вероятностью Р принимается, и функцию F(x) можно использовать для описания статистического распределения, если

> ., то гипотеза с вероятностью Р отвергается и выбранную теоретическую функцию распределения F(x) нельзя использовать для описания статистического распределения.

Критерий Колмогорова своей простотой выгодно отличается от описанного ранее критерия ², поэтому его часто применяют на практике. Однако этот критерий можно применять только в том случае, когда гипотетическое распределение F(x) полностью известно из каких-либо теоретических соображений. Такой случай на практике встречается довольно редко. Обычно известен только общий вид функции распределения F(x), а входящие в нее числовые параметры (у нормального закона это 2 параметра: математическое ожидание и дисперсия) определяются по исследуемому статистическому материалу.

При применении критерия Пирсона это обстоятельство учитывается соответствующим уменьшением числа степеней свободы распределения ². Критерий же Колмогорова такого не предусматривает. Если все же применять этот критерий в тех случаях, когда параметры теоретического распределения выбираются по статистически данным, критерий дает заведомо завышенные значения вероятности . Поэтому в ряде случаев мы рискуем принять неверную гипотезу за верную.