Значения критерия Шарлье
-
n
5
10
20
30
40
50
100
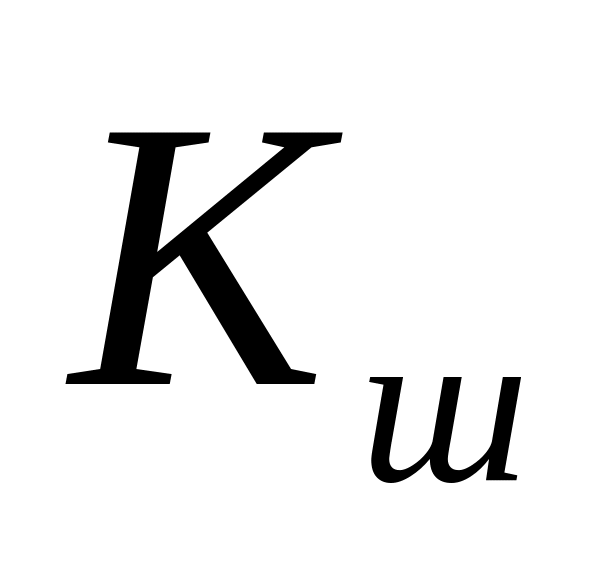
1,3
1,65
1,96
2,13
2,24
2,32
2,58
Вариационный
критерий Диксона Кд
удобный и достаточно мощный (с малыми
вероятностями ошибок). Применяется при
числе наблюдений n
< 30. При его применении полученные
результаты наблюдений записывают в
вариационный возрастающий ряд
.
Критерий Диксона определяется как
Критическая область для этого критерия
.
Значения
zq
приведены
в табл.2.4.
Пример 2. Было проведено пять измерений напряжения в электросети. Получены следующие результаты: 127,1; 127,2; 126,9; 127,6; 127,2. Результат 127,6В существенно (на первый взгляд) отличается от остальных. Проверить, не является ли он промахом.
Решение. Составим вариационный ряд из результатов измерений напряжения в электросети:
126,9; 127,1; 127,2; 127,2; 127,6. Для крайнего члена этого ряда 127,6 критерий Диксона
Кд = (127,6 – 127,2) / (127,6 – 126,9) = 0,4 / 0,7 = 0,57.
Таблица 2.4
Значения критерия Диксона
n |
при q, равном |
|||
0,10 |
0,05 |
0,02 |
0,01 |
|
4 |
0,68 |
0,76 |
0,85 |
0,89 |
6 |
0,48 |
0,56 |
0,64 |
0,70 |
8 |
0,40 |
0,47 |
0,54 |
0,59 |
10 |
0,35 |
0,41 |
0,48 |
0,53 |
14 |
0,29 |
0,35 |
0,41 |
0,45 |
16 |
0,28 |
0,33 |
0,39 |
0,43 |
18 |
0,26 |
0,31 |
0,37 |
0,41 |
20 |
0,26 |
0,30 |
0,36 |
0,39 |
30 |
0,22 |
0,26 |
0,31 |
0,34 |
Как следует из табл.2.4, по этому критерию результат 127,6В может быть отброшен как промах лишь на уровне значимости q = 0,10.
Применение рассмотренных критериев требует осмотрительности и учета объективных условий измерения. Оператор должен исключить результат наблюдения с явной грубой погрешностью и выполнить новое измерение. Но нельзя просто отбрасывать более или менее сильно отличающиеся от других результаты наблюдений. В сомнительных случаях лучше сделать дополнительные измерения (не взамен сомнительных, а кроме них) и затем использовать рассмотренные критерии.
2.1.5. Суммирование погрешностей
Суммирование систематических погрешностей.
Неисключенная систематическая погрешность результата измерения включает составляющие, обусловленные методом, средствами измерений и другими источниками. Если случайные погрешности малы, то в качестве границ неисключенной систематической погрешности принимают пределы допускаемых основных и дополнительных погрешностей СИ.
При суммировании неисключенных систематических погрешностей их рассматривают как случайные величины с равномерным законом распределения.
1. Границы неисключенных систематических погрешностей результата измерения определяются по формуле
,
где
-
граница i
– й неисключенной систематической
погрешности;
- число неисключенных систематических погрешностей;
- коэффициент, зависящий от числа слагаемых , их соотношения и доверительной вероятности Р.
2. При Р < 0,99 коэффициент k мало зависит от и может быть представлен усредненными значениями, приведенными в табл. 2.5. Их погрешность не превышает 10%.
Таблица 2.5