12

МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ

Національний університет “Львівська політехніка”

ДОСЛІДЖЕННЯ ПРОСТОРОВОЇ

ПЕРЕХІДНОЇ ХАРАКТЕРИСТИКИ

Методичні вказівки

до лабораторної роботи з дисципліни

"Основи телебачення"

для студентів базового напряму 0907 "Радіотехніка"

спеціальності 7.090701 "Радіотехніка"

Затверджено

на засіданні кафедри

радіоелектронних пристроїв та систем

Протокол № 9 від 12.01.2011 р.

Львів – 2011

Дослідження просторової перехідної характеристики. Методичні вказівки до лабораторної роботи з дисципліни "Основи телебачення” для студентів базового напрямку 0907 “Радіотехніка” спеціальності 7.090701 “Радіотехніка” //Укл. Мінзюк В.В., Шклярський В.І. Львів: Видавництво Національного університету “Львівська політехніка”, 2011. – 11 с.

Укладачі: Мінзюк В.В., асист.

Шклярський В.І., к.т.н., доц.

Відповідальний за випуск І.Н. Прудиус, докт. техн. наук, проф.

Рецензенти Гоблик В.В., к.т.н., доц.

Оборжицький В.І.., к.т.н., доц.

1.Мета роботи

Метою роботи є дослідження впливу розміру скануючого елемента на перехідну характеристику телевізійної системи.

2.Теоретична частина

Нехай об’ємом, зображення якого має передати телевізійна система, є поділене навпіл поле, ліва частина якого має яскравість рівну нулю, а права – певну постійну яскравість у відповідності з рис. 1,а.

Рис.1. Просторова перехідна характеристика телевізійної системи

Такий характер розподілу яскравості ілюструється ламаною лінією 1 на рис. 1,б. Ідеальна телевізійна система повинна забезпечувати такий же характер розподілу яскравості на приймальній стороні, наприклад, на екрані кінескопа. В реальній телевізійній системі розподіл яскравості відповідає кривій 2, яка свідчить про те, що система неспроможна передати різкий перепад яскравості, зображення на приймальній стороні не буде мати чітких границь, вони будуть “розмитими”. Криву 2 називають просторовою перехідною характеристикою телевізійної системи від світла до світла і кажуть, що нею визначається різкість телевізійного зображення. Чим більшою є крутість перехідної характеристики, тим вища різкість телевізійного зображення.

Така перехідна характеристика є результуючою часткових перехідних характеристик, а саме:

- просторової перехідної характеристики об’єктиву, який формує зображення об’єкту на світлочутливій поверхні перетворювача світло-сигнал;

- часовою перехідною характеристикою каналу зв’язку між передавальною і приймальною сторонами;

- просторовою перехідною характеристикою перетворювача сигнал-світло (кінескопа або електронно-променевої трубки).

Зауважимо, що взаємний перехід між просторовою та часовою перехідними характеристика базується на пропорційності х = υt, де х  коефіцієнт пропорційності, υ – швидкість руху сканую чого елемента в напрямі осі t.

Кожна ð–характеристик вносить свій вклад в зменшення крутості результуючої перехідної характеристики.

В цій лабораторній роботі досліджується просторова перехідна характеристика перетворювача світло-сигнал фототелевізійного типу, структурна схема якого показана на рис. 2, де СЕПТ – скануюча електронно-променева трубка, на екрані якої формується скануюча світлова пляма, ПО – проекційний об’єктив, що створює зображення плями в площині об’єкту 0, який відповідає рис. 1,а:

Рис.2. Структурна схема перетворювача світло-сигнал

ФЕП – фотоелектричний перетворювач, що формує відеосигнал, який далі (після відповідних перетворень) поступає в канал зв’язку.

Нехай прозорість в площині об’єкта описується законом Е(х,у), а розподіл енергії в скануючій плямі законом ρ(х, у).Зміст координат х, у та х, у пояснюється рисунком 3 , де l та h - відповідно ширина та висота поля об’єкта , в межах якого здійснюється сканування , ∆S – площа сканую чого елемента , ds – елементарна ділянка, в межах якої прозорість E можемо вважати постійною.

Рис.3. До визначення координат об’єкта

В межах ділянки ds скануючи пляма створює світловий потік dΦ, і маємо певну прозорість об’єкта, яка характеризується світловим потоком dФ, тобто

.

На підставі цього виразу

Потрапляючи на ФЕП, цей елементарний світловий потік викличе появу елементарного фотоструму

,

де ε - інтегральна чутливість ФЕП,

k – коефіцієнт, що враховує втрати світлового потоку, які мають місце між об’єктом і ФЕП.

З урахуванням всієї площі скануючої плями ∆S повний струм на виході ФЕП буде рівний.

.

Якщо прозорість об’єкта в межах робочого поля є постійною, то

.

де - повна енергія скануючої плями.

Нехай тепер прозорість об’єкта в межах поля не є постійною, а стрибкоподібно змінюється на границі АВ від значення Е=0 до значення Е=соnst, як це показано на рис.4,а.

Перехід симетричної плями а радіусом r і розподілом енергії через границю АВ викличе зміну струму ФЕП, тобто струм стане функцією координати плями х:

.

Миттєві значення цього струму пропорційні енергії тієї частини плями, яка знаходиться на прозорій частині об’єкта. Цю енергію знайдемо так. Виділимо в межах цієї частини плями безмежно вузьку смужку dx (див.рис.4 ,а).Її інтегральна енергія

Рис. 4. До сканування об’єкта з різною прозорістю

Враховуючи, що центр плями знаходиться на віддалі х від границі АБ, а виділена смужка dx на віддалі х від рухомого центра плями , знайдемо шукану частину енергії плями. З врахуванням одержаних виразів

.

де εkEP - енергія всієї плями.

Як було показано вище, εkEP – це значення струму ФЕП при прозорому об’єкті, або, іншими словами, значення усталеного струму(після переходу границі) . Поділивши і(х) на , одержимо шукану перехідну характеристику

З останнього виразу бачимо, що перехідна характеристика залежить від розміру скануючої плями r (див. вираз для Р) та закону розподілу енергії в плямі ρ(х, У) (див. вираз для R(x)).

Нехай пляма має форму квадрата з розміром сторони δ, енергія в межах плями розподілена рівномірно, як це показано на рис. 5, а, тобто

Рис.5. До розподілу скануючої плями у вигляді квадрата

тоді

,

.

і перехідна характеристика h(x) має вигляд, показаний на рис. 5, в. Це означає, що при такій скануючій плямі різкий чорно-білий перепад в прозорості об’єкта дасть сигнал, який при відтворенні об’єкта буде мати зони розмиття границі з лінійною зміною інтенсивності, а розмір зони розмиття буде рівний розміру скануючого елемента δ.

Реальні скануючі плями мають розподіл енергії, близький до показаного на рис. 4,а. Часто його апроксимують так званим гаусівським законом

де - умовний радіус плями, що відповідає рівневі ≈0,37 від максимального.

В цьому випадку перехідна характеристика

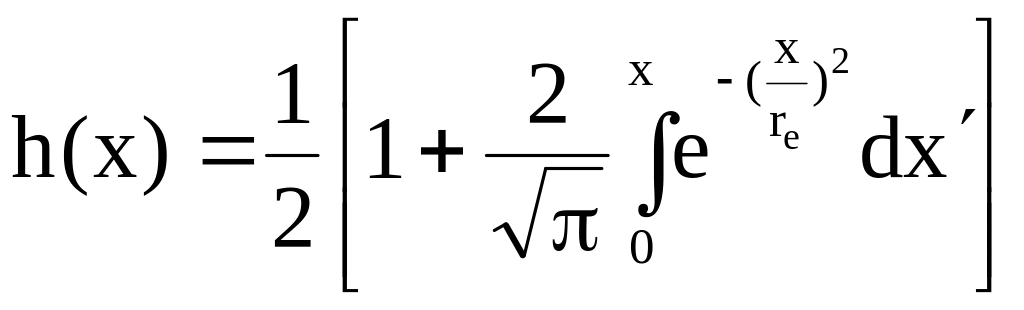
Вона має вигляд, близький до показаного на рис.4 в. Оскільки пляма при такому законі розподілу енергії не має чітких границь ( ρ стає рівним нулю при безмежних значення (х та у), то і межі розмиття переходу є невизначеними. За ширину зони розмиття приймають умовно ту, що відповідає рівним 0.08 та 0.92 перехідної характеристики. При цьому вона приблизно рівна 2 .