1. Если один из углов равнобедренного треугольника равен 100°, то другой его угол равен 40°.

2. Если два треугольника подобны, то их соответствующие стороны равны.

3. Если основания трапеции равны 2 и 8, то средняя линия этой трапеции равна 5.

№6 Какой угол (в градусах) образуют минутная и часовая стрелки, когда часы показывают ровно 11 часов?

№7 Основания равнобедренной трапеции равны 9 и 21, а ее периметр равен 50. Найдите площадь трапеции.

№8 На стороне АС треугольника АВС отмечены точки D и E так, что AD=CE. Докажите, что если AB=BC, то BD=BE.

Вариант 4.

№1 В окружности с центром О AC и BD – диаметры. Центральный угол AOD равен 132°. Найдите вписанный угол ACB.

№2 В треугольнике АВС угол С равен 90°, АС=8, cosA= . Найдите АВ.

№3 Стороны параллелограмма равны 10 и 35. Высота, опущенная на первую сторону, равна 21. Найдите высоту, опущенную на вторую сторону.

№4 На клетчатой бумаге с размером клетки 1см х 1см изображена трапеция. Найдите ее площадь.

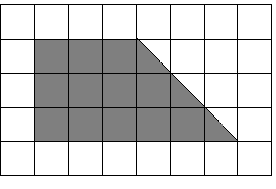
№5 Какие из утверждений верны?

1. Центром симметрии квадрата является точка пересечения диагоналей.

2. Если две стороны треугольника равны 3 и 5, то его третья сторона больше 2.

3. Если в четырехугольнике две стороны параллельны, то это четырехугольник – параллелограмм.

№6 Какой угол (в градусах) образуют минутная и часовая стрелки, когда часы показывают ровно 8 часов?

№7 Основания равнобедренной трапеции равны 12 и 24, а ее периметр равен 56. Найдите площадь.

№8 На стороне АС треугольника АВС отмечены точки D и Е так, что AD=CE. Докажите, что если BD=BE, то AB=BC.

Вариант 5.

№1 В окружности с центром О AC и BD – диаметры. Центральный угол AOD равен 132°. Найдите вписанный угол ACB.

№2 В треугольнике ABC угол C равен 90°, АС=15, cosA= . Найдите AB.

№3 Стороны параллелограмма равны 32 и 64. Высота, опущенная на первую сторону, равна 48. Найдите высоту, опущенную на вторую сторону параллелограмма.

№4 На клетчатой бумаге с размером клетки 1см х 1см изображена трапеция. Найдите ее площадь.

№5 Какие из следующих утверждений верны?

4. Если радиус круга равен 4, то его площадь равна 8.

5. Любой равнобедренный треугольник имеет не менее одной оси симметрии.

6. Если угол одного треугольника равен углу другого треугольника, то такие треугольники подобны

№6 Какой угол (в градусах) образуют минутная и часовая стрелки, когда часы показывают ровно 11 часов?

№7 Основания равнобедренной трапеции равны 8 и 18, а ее периметр равен 52. Найдите площадь трапеции.

№8 На стороне AC треугольника ABC отмечены точки D и E так, что AD=CE. Докажите, что если AB=BC, то BD=BE.

В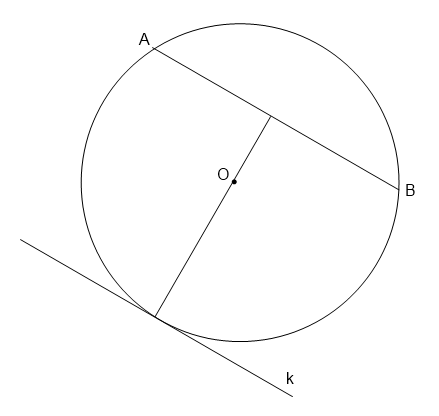 ариант 6.

1. Радиус окружности с центром в точке O равен 13 см, длина хорды AB равна 24 см. Найдите расстояние от хорды AB до параллельной ей касательной K (см. рисунок.)

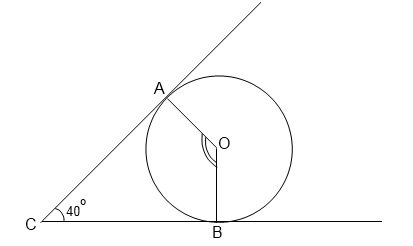
2. В угол C величиной 40° вписана окружность, которая касается сторон угла в точках A и B.

Найдите величину угла AOB в градусах.

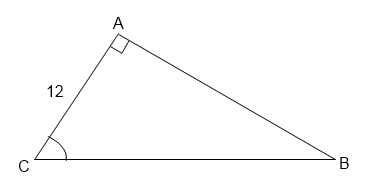
3. В треугольнике ABC угол A прямой, AC = 12, cos угла ACB = 0,6. Найдите BC.

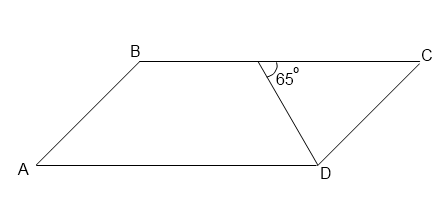
4. Найдите величины углов параллелограмма ABCD, если биссектриса угла D образует со стороной BC угол, равный 65°.

5. Укажите в ответе номера верных утверждений:

1) В любом выпуклом четырехугольнике все углы острые.

2) Существует выпуклый четырехугольник, все углы которого острые.

3) В любом четырехугольнике все углы прямые.

4) Существует выпуклый четырехугольник, все углы которого прямые.

6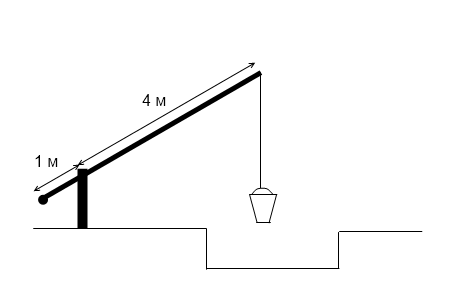 . На рисунке изображен колодец с «журавлем». Короткое плечо имеет длину 1 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м ?

7. На сторонах угла BAC, равного 40°, и на его биссектрисе отложены равные отрезки AB, AC и AD. Определите величину угла BDC.

8. Докажите, что у равных треугольников ABC и MNK медианы, проведенные из вершин A и M, равны.

В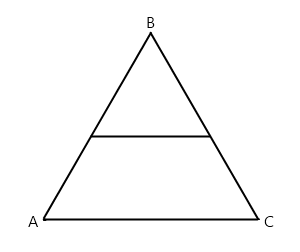 ариант 7.

1. Периметр равностороннего треугольника ABC равен 24 см. Найдите длину средней линии этого треугольника.

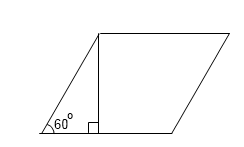
2. Сторона ромба равна 32, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков.

3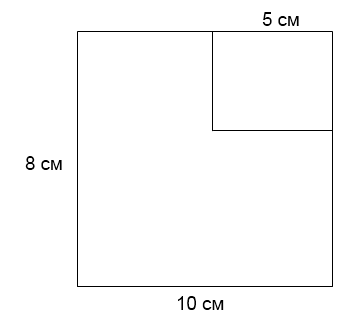 . Из прямоугольника со сторонами 10 см и 8 см вырезан квадрат со стороной 5 см. Найдите площадь оставшейся части. Ответ дайте в см².

4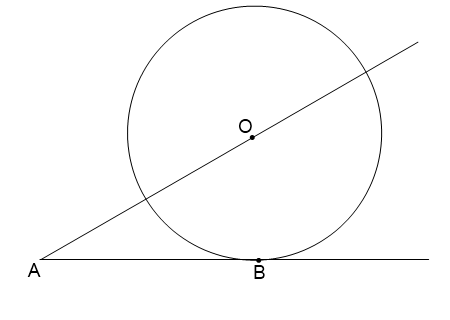 . К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 15, AO = 17см.

5. Укажите в ответе номера верных утверждений:

1) Существует прямоугольник диагонали которого перпендикулярны.

2) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

3) Если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники равны.

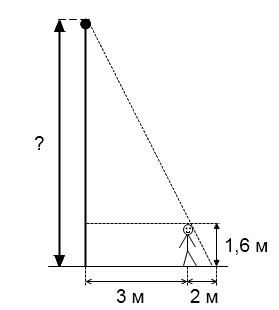
6. Человек, рост которого 1.6 м, стоит на расстоянии 3 м от уличного фонаря. При этом длина его тени равна 2 м. Определите высоту фонаря (в м).

7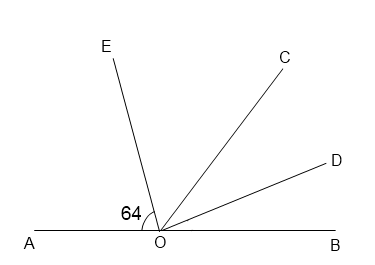 . Найдите величину угла DOB, если OE — биссектриса угла AOC, OD — биссектриса угла COB.

8. В параллелограмме ABCD точка M — середина стороны AB. Известно, что MC = MD. Докажите, что данный параллелограмм — прямоугольник.

Вариант 8.

1. Периметр равностороннего треугольника ABC равен 36 см. Найдите длину средней линии этого треугольника.

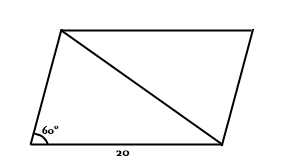
2.Сторона ромба равна 20, а острый угол равен 60°. Найдите

длину меньшей диагонали ромба.

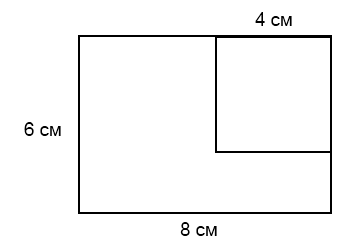
3.Из прямоугольника со сторонами 6 см и 8 см вырезан квадрат со стороной 4 см. Найдите площадь оставшейся части. Ответ дайте в см².

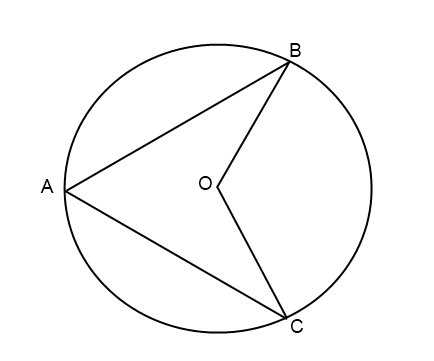
4.Точка О — центр окружности, угол BAC = 70° (см. рисунок). Найдите величину угла BOC (в градусах).

5. Укажите в ответе номера неверных утверждений.

1) Два угла с общей стороной называются смежными.

2) На прямой можно отложить только один отрезок заданной длины.

3) Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

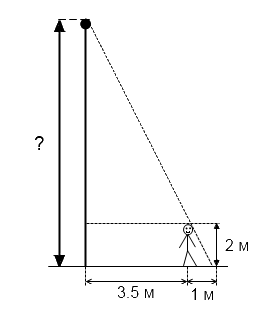
6. Человек, рост которого 2 м, стоит на расстоянии 3,5 м от уличного фонаря. При этом длина его тени равна 1 м. Определите высоту фонаря (в м).

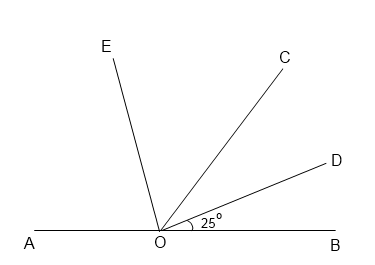
7. Найдите величину угла AOE, если OE – биссектриса угла AOC, OD — биссектриса угла COB.

8. В параллелограмме ABCD точка K – середина стороны AB. Известно, что KC = KD. Докажите, что данный параллелограмм — прямоугольник.

В ариант 9.

1. Средняя линия равностороннего треугольника ABC равна 8 см. Найдите периметр этого треугольника.

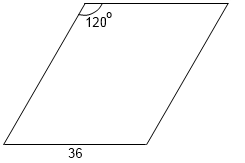
2. Сторона ромба равна 36, а тупой угол равен 120°. Найдите длину меньшей диагонали ромба.

3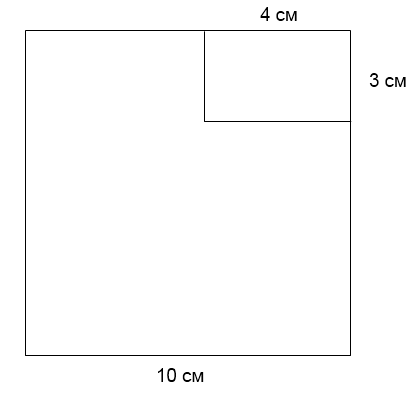 . Из квадрата со стороной 10 см вырезан прямоугольник со сторонами 3 см и 4 см. Найдите площадь оставшейся части. Ответ дайте в см².

4. Точка O — центр окружности, угол BAC = 75° (см. рисунок).

Найдите величину угла BOC (в градусах).

5. Укажите в ответе номера верных утверждений:

1) Существует параллелограмм, диагонали которого равны.

2) Через точку, лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.

3) Если две стороны одного треугольника соответственно равны двух сторонам другого треугольника, то такие треугольники равны.

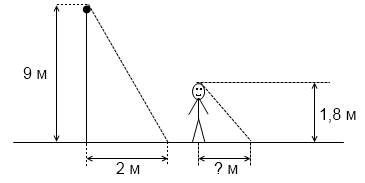
6. Столб высотой 9 м отбрасывает тень длиной 2 м. Найдите длину (в м) тени человека ростом 1,8 м, стоящего около этого столба.

7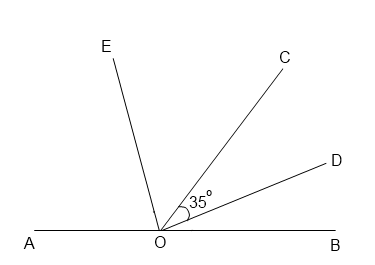 . Найдите величину угла COE, если OE — биссектриса угла AOC, OD – биссектриса угла COB.

8. Противоположные углы четырехугольника попарно равны. Докажите, что этот четырехугольник — параллелограмм.

Вариант 10.

1. Средняя линия равностороннего треугольника ABC равна 7 см. Найдите периметр этого треугольника.

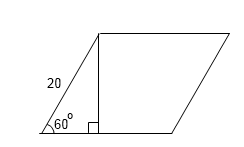
2. Сторона ромба равна 20, а острый угол равен 60° . Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?

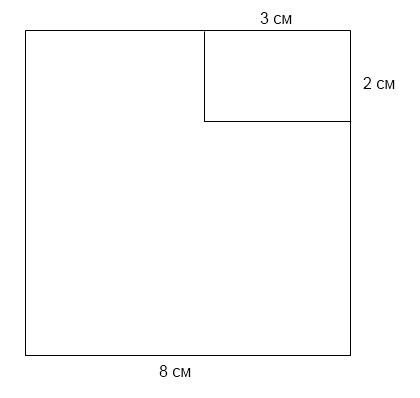
3. Из квадрата со стороной 8 см вырезан прямоугольник со сторонами 3 см и 2 см. Найдите площадь оставшейся части. Ответ дайте в см².

4 . К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.

5. Укажите в ответе номера верных утверждений:

1) Если у параллелограмма есть один прямой угол, то этот параллелограмм — прямоугольник.

2) Через две точки плоскости можно провести две различные прямые.

3) Если две стороны и угол между ними одного треугольника, соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

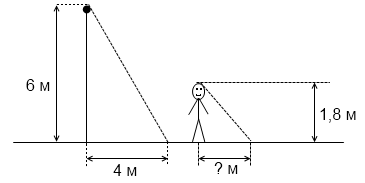
6. Столб высотой 6 м отбрасывает тень длиной 4 м. Найдите длину (в м) тени человека ростом 1,8 м, стоящего около этого столба.

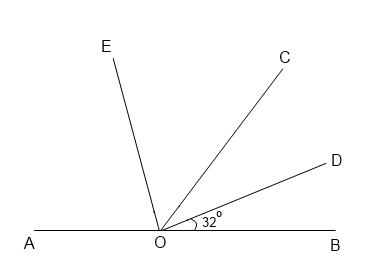
7. Найдите величину угла COE, если OE — биссектриса угла AOC, OD — биссектриса угла COB.

8. Середина стороны параллелограмма равноудалена от концов его противоположной стороны. Докажите, что данный параллелограмм — прямоугольник.