4.2. Проектирование синхронных пересчетных схем

Поскольку пересчётные схемы, также как и сдвигающие регистры, относятся к классу последовательностных схем, то все замечания, касающиеся проектирования регистров, справедливы и для проектирования пересчётных схем.

Задание на курсовое проектирование предусматривает синтез реверсивной пересчётной схемы, вырабатывающей заданную последовательность двоичных эквивалентов чисел. В качестве примера рассмотрим проектирование пересчётной схемы, реализующей следующую последовательность двоичных эквивалентов чисел

3, 7, 5, 0, 6, 4, 2, (5)

в которой предусмотрена возможность реверса, т.е. изменение порядка работы схемы на обратный

2, 4, 6, 0, 5, 7, 3. (6)

Так как число выполняемых счётчиком операций К=2 (прямой счёт и обратный счёт), то в соответствии с (1) потребуется одна управляющая переменная у. Условимся, что при y=0 счётчик будет вырабатывать последовательность чисел (5), а при у=1 последовательность чисел (6). Описание работы счётчика представим в виде таблицы 6.

Вследствие нерегулярности структуры пересчётных схем при их описании необходимо рассматривать поведение каждого разряда счётчика в отдельности. Количество разрядов счётчика определяется как

n = ] log (N_max + 1) [,

где N _mах - максимальное число в заданной последовательности. Для рассматриваемого примера N _mах=7, следовательно,

n = ] log (7+1) [ =3.

Обозначим выходные сигналы каждого разряда счётчика как Q₁, Q₂, Q₃ (Q₁-старший разряд, Q₃ - младший разряд). В столбцах Q₁, Q₂, Q₃ табл. 6 перечислены разрешенные комбинации выходных сигналов счётчика. Порядок следования этих комбинаций строго определен выражениями (5), (6) и значениями переменной у.

Так, при у=1 вслед за комбинацией сигналов Q₁=0, Q₂=1, Q₃=1, (число 3) следует комбинация Q₁=1, Q₂=1, Q₃=1 (число 7) и т. д. В столбцах _Q1, _Q2, _Q3 указан тип перехода, который осуществляется каждым разрядом счётчика при соответствующем изменении состояния этого счётчика. Тип перехода определяется сравнением значений Q₁, Q₂, Q₃ в рассматриваемом состоянии счётчика со значениями этих сигналов в следующем состоянии пересчётной схемы. Так, рассматривая состояние №=1, которое характеризуется значениями выходных переменных Q₁=0, Q₂=1, Q₃=1 и состояние №=2, при котором Q₁=1, Q₂=1, Q₃=1, определяем, что первый разряд пересчётной схемы при переходе этой схемы из состояния №=1 в состояние №=2 должен осуществить переход из 0 в 1, т.е. переход типа .

Аналогично определяются типы переходов которые осуществляют второй (переход типа 1) и третий (переход типа 1) разряды счётчика. Полученная информация заносится в первую строку табл. 6. Используя карту Карно для четырех переменных, опишем поведение каждого разряда счётчика. Информация для заполнения карт аналогичен ранее рассмотренному случаю описания поведения i-го разряда сдвигающего регистра. Карты Карно, описывающие поведение 1-го, 2-го и 3-го разрядов проектируемого реверсивного счетчика представлены на рис. 7.

Q₁- карта Q₂ - карта Q₃- карта

yQ1 Q2Q3	00	01	11	10
00			1	
01	x		1	x
11		1		0
10	0	1		

yQ1 Q2Q3	00	01	11	10
00				0
01	x	0		x
11	1		1	1
10	1			

yQ1 Q2Q3	00	01	11	10
00	0	0	0	
01	x		1	x
11	1	1	1	
10		0	0	0

Рис. 7

Таблица 6

Описание синхронного реверсивного счётчика

№
сост.	у	Q1	Q2	Q3	Q1	Q2	Q3
1	0	0	1	1		1	1
2	0	1	1	1	1		1
3	0	1	0	1		0	
4	0	0	0	0			0
5	0	1	1	0	1		0
6	0	1	0	0			0
7	0	0	1	0	0	1	
Х	Х	Х	Х	Х	Х	Х	Х
8	1	0	1	0			0
9	1	1	0	0	1		0
10	1	1	1	0			0
11	1	0	0	0		0	
12	1	1	0	1	1		1
13	1	1	1	1		1	1
14	1	0	1	1	0	1	
Х	Х	Х	Х	Х	Х	Х	Х

В качестве примера рассмотрим схемную реализацию проектируемого счетчика на базе D и JK- триггеров, словарное описание которых приведено в табл. 7. После выполнения операции подстановки в карты Карно (рис.7) значений входных сигналов триггеров из табл. 5, состояние входов триггеров трех разрядов счётчика будут характеризоваться соответствующими картами Карно, приведенными на рис.8 для D- триггера и на рис.9 для JK-триггера.

D₁- карта D₂ – карта D₃ - карта

yQ1 Q2Q3	00	01	11	1 0
0 0	1	0	1	1
01	x	0	1	x
11	1	1	0	0
10	0	1	0	1

yQ1 Q2Q3	00	01	11	10
00	1	1	1	0
01	x	0	1	x
11	1	0	1	1
10	1	0	0	0

yQ1 Q2Q3	00	01	11	10
00	0	0	0	1
01	x	0	1	x
11	1	1	1	0
10	1	0	0	0

Рис. 8

J₃ - карта J₁ – карта J₂ – карта

yQ1 Q2Q3	00	01	1 1	10
00	1	x	x	1
01	x	x	x	x
11	1	x	x	0
10	0	x	x	1

yQ1 Q2Q3	0 0	01	11	10
00	1	1	1	0
01	x	0	x	x
11	x	x	x	x
10	x	x	x	x

yQ1 Q2Q3	00	01	11	10
00	0	0	0	1
01	x	x	x	x
11	x	x	x	x
10	1	0	0	0

K₁- карта К₂ - карта К₃ - карта

yQ1 Q2Q3	00	01	11	10
00	x	1	0	x
01	x	1	0	x
11	x	0	1	x
10	x	0	1	x

yQ1 Q2Q3	00	01	1 1	10
00	x	x	x	x
01	x	x	x	x
11	0	1	0	0
10	0	1	1	1

yQ1 Q2Q3	00	01	11	10
00	x	x	x	x
01	x	1	0	x
11	0	0	0	1
10	x	x	x	x

Рис.9

Проведя склеивание, как это показано на рис. 8 и рис. 9, получим следующие выражения

D₁ =yQ₁Q₂ +y Q₂ Q₃ + y Q₁Q₂ +yQ₂ + yQ₁Q₃,

D₂= y Q₁ + Q₁ Q₂ Q₃ + yQ₃,

D₃= yQ₁ Q₂ +y Q₂ Q₃ + yQ₁ Q₃ + yQ₁Q₂,

J₁= Q₂ + yQ₃ + yQ₃,

K₁ =yQ₂ + yQ₂,

J₂=yQ₁ + yQ₃,

K₂= yQ₁ + yQ₃,

J₃=yQ₁Q₂ + yQ₁ Q₂,

K₃=yQ₁ + yQ₂.

Преобразуем полученные функции в базис И-НЕ

---------- -------- ------- ----- ----------

D₁=yQ₁Q₂ yQ₂ Q₃ yQ₁ Q₂ yQ₂ yQ₁Q₃,

----- ------------- ----

D₂=yQ₁ Q₁Q2Q3 yQ₃,

---------- -------- -------- ----------

D₃ = yQ₁ Q₂ y Q₂ Q₃ y Q₃ Q₁ yQ₁Q₂,

----- ------ ----- -----

J₁ = Q₂ yQ₃ y Q₃, K₁ = yQ₂ y Q₂,

---- ----- ----- -----

J₂ = y Q₁ yQ₃ K ₂= yQ₁ yQ₃,

J₃ = yQ₁Q₂ yQ₁ Q₂, K₃ = y Q₁ yQ₂.

Проведем оценку сложности комбинационных схем управления в полученных счётчиках. Для счётчика, реализованного на базе триггеров, сложность определяется суммой

SD=(2+1+1) + (2+1+1) + (2+1+1) + (1+1) + (1+1+1) + (1+1+1+1+1) + (2+1) + (1+1+1) + (1+1) + (1+1+1) + (2+1+1) + (2+1+1) + (1+1+1) + (1+1+1) + (1+1+1+1) = 51,

а для счётчика, реализованного на базе JK -триггеров, составит

SJK = 1 + (2+1) + (1+1) + (1+1+1) + (2+1) + (1+1) + (1+1) + (1+1) + (2+1) + (1+1) + (2+1) + (1+1) + (1+1) + (1+1+1) + (2+1+1) + (1+1) + (1+1) + (2+1) + (1+1) = 46.

Как и при оценке сложности схемы управления регистром, в данном случае необходимо учитывать, что поскольку для получения сигналов Q₁, Q₂, Q₃ не требуется дополнительных затрат, то эти входы при вычислении SD и SJK оценены по 1.

Сравнение оценок сложности схем показывает, что SD < SJK, следовательно, для реализации пересчётной схемы целесообразно выбрать триггер JK - типа.

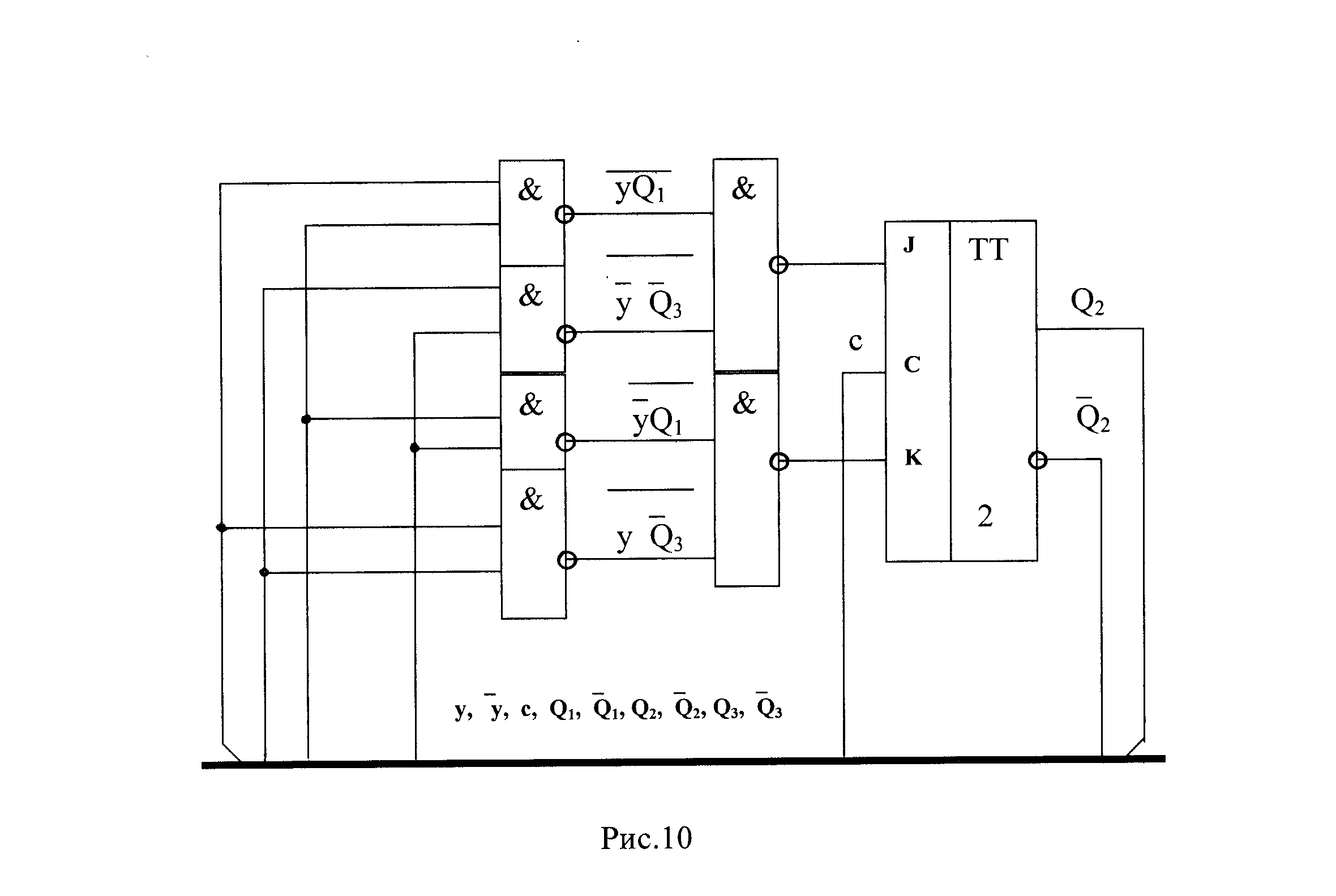
Фрагмент схемы счётчика, построенный по полученным выражениям для JK-триггера приведен на рис. 1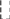0.