5.7 Розрахунок параметрів і характеристик виробничої функції

На основі відібраного виду рівняння та початкових даних розраховуються первинні параметри виробничої функції (а₀, а_і).

Параметри рівняння, зазвичай, розраховуються методом найменших квадратів, який передбачає мінімізацію суми квадратів відхилень між фактичними і розрахунковими значеннями результативного показника

.

Якщо у попередній вираз підставити рівняння зв’язку , отримаємо

.

В умові (2.6) у_і та х_і є відомими величинами, а параметри рівняння а₀, а_і - невідомими константами.

Для їх обчислення необхідно прирівняти до нуля частинні похідні від виразу (2.6) по кожній шуканій константі окремо. Після відповідних перетворень одержують систему нормальних рівнянь, яка для багатофакторних моделей має такий вигляд:

(2.7)

Логарифмічні і степеневі рівняння слід спочатку перетворити у лінійне рівняння. Для цього степенева модель перетворюється у логарифмічну шляхом логарифмування лівої і правої частини рівняння, а потім умовно позначивши , отримаємо лінійне рівняння

.

Для парного лінійного рівняння система нормальних рівнянь має вигляд:

Оскільки в нормальних рівняннях невідомими є а₀ і а₁, то для спрощення їх розрахунків можна скористатися детермінантами (правило Кремера)

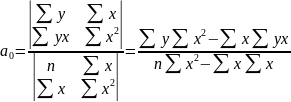, (2.8)

Всі похідні параметри рівняння, методи розрахунку та їх економічна інтерпретація наведені в параграфі 1.4.

Крім перерахованих параметрів рівняння - первинних і вторинних - варто звернути увагу на -коефіцієнт, який характеризує зв'язок сили впливу кожного фактора на рівень досліджуваного показника спільно з їх мінливістю. Він дозволяє оцінити реальну можливість "покращення" об'єкта дослідження за рахунок зміни певного фактора. -коефіцієнт розраховується за формулою

, (2.9)

де , – середнє квадратичне відхилення відповідного і-го фактора і результативного показника.

-коефіцієнт показує, на яку частину середньоквадратичного відхилення зміниться результативний показник зі зміною на одну середньоквадратичну відповідного фактора за фіксованого значення решти факторів.

Параметри рівняння - первинні і вторинні - дозволяють оцінити вплив кожного фактора на рівень результативного показника. Однак вони не в змозі оцінити ступінь сили взаємозв'язку і взаємозалежності між результативним показником і факторами, що визначають його рівень. Сила взаємозв'язку або тіснота зв'язку по суті визначають якість рівняння, теоретичну і практичну цінність його. Під тіснотою або силою взаємозв'язку розуміється статистична величина, яка характеризує розкид всієї сукупності фактичних даних відносно лінії, отриманої на основі кореляційного рівняння.

Показниками тісноти зв'язку є: для парного лінійного рівняння – коефіцієнт парної кореляції (r); для багатофакторного лінійного рівняння – коефіцієнт множинної лінійної кореляції (R); для нелінійних рівнянь – парних і множинних – відповідно парнe і множинне кореляційне відношення ( ).

Парний лінійний коефіцієнт кореляції розраховується за формулою

(2.10)

Множинний лінійний коефіцієнт кореляції, кореляційне відношення – парне і множинне – розраховуються за єдиною формулою

(2.11)

Показники тісноти зв'язку змінюються в таких інтервалах:

-1 ≤ ≤ +1

0 ≤ ≤ +1

Про тісноту зв'язку роблять висновки з таких значень показ­ників:

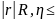0,5 – зв'язок слабкий;

0,7 ≥ ≥ 0,5 – зв'язок середній;

≥ 0,7 – зв'язок сильний.

У багатофакторних рівняннях множинний коефіцієнт кореляції (множинне кореляційне відношення) характеризує ступінь сукупного впливу факторів, включених в модель, на рівень результативного показника.

Чим вище тіснота зв'язку, тобто чим більша величина множин­ного лінійного коефіцієнта кореляції (множинного кореляційного відношення), тим вище аналітична і передбачувальна можливість побудованого рівняння.

Про частку впливу відібраних у рівняння виробничої функції факторів на величину результативного показника свідчить коефіцієнт детермінації, який є множинним коефіцієнтом кореляції (множинне кореляційне відношення) у квадраті (R², ).

У багатофакторних рівняннях по парних коефіцієнтах кореляції безпосередньо неможливо судити про ступінь тісноти певного фактора з результативним показником, оскільки парні коефіцієнти кореляції відображають не тільки безпосередній вплив даного фактора на результативний показник, але й опосередкований вплив на нього через даний фактор з боку інших факторів, або, іншими словами, парні коефіцієнти кореляції у багатофакторних моделях характеризують зв'язки з урахуванням взаємодії різних факторів [48].

Щоб оцінити вплив окремо взятого фактора на результативний показник у "чистому" виді і позбутися від супутніх впливів інших факторів, розраховується частинний коефіцієнт кореляції (ȓ)

(2.12)

За значеннями частинних коефіцієнтів кореляції можна достатньо точно зробити висновки щодо сили зв'язку результативного показника з кожним окремим показником.

Частинні коефіцієнти кореляції зазвичай відрізняються від парних: вони можуть бути менші або більші, а у виняткових випадках рівні.

Крім тісноти зв'язку для оцінки адекватності рівняння реальним процесам служать показники, вказані нижче.

Середня помилка апроксимації

(2.13)

Середнє квадратичне відхилення між фактичними і розрахунковими значеннями функції:

а) абсолютне

(2.14)

б) відносне

(2.15)

Середнє відхилення між фактичними і розрахунковими значеннями функції:

а) абсолютне

(2.16)

б) відносне - визначається аналогічно середній помилці апроксимації

Залишкова дисперсія

(2.13).

де m – число факторів, які включені у склад моделі.

Чим менше значення перерахованих показників (2.13 - 2.17), тим вище якість відібраного для дослідження рівняння.

Допустимий рівень наведених вище показників установлює дослідник, опираючись на досвід, знання і особливість досліджуваного явища (процесу), оскільки науково обґрунтованих рекомендацій відносно меж цих показників немає. Кожен дослідник вибирає як пріоритетний будь-який показник, виходячи із власного розуміння і досвіду.