Задание 1.

Имеются данные численности наличного населения города Г за 2003–2011 гг. (на начало года), тыс. чел.

2003	2004	2005	2006	2007	2008	2009	2010	2011
106,8	106	105,4	103	102,8	102,7	102,7	102,6	102,5

1. Постройте прогноз численности наличного населения города Г на 2012-2013 гг., используя методы: скользящей средней, экспоненциального сглаживания, наименьших квадратов.

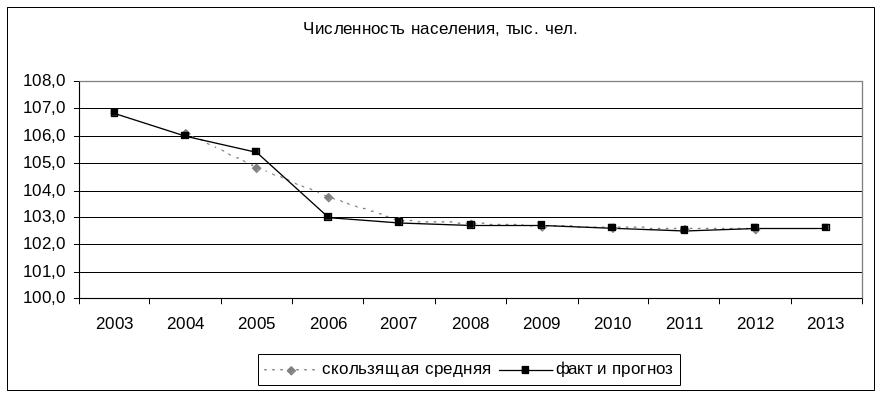
2. Постройте график фактического и расчетных показателей

3. Рассчитайте ошибки полученных прогнозов при использовании каждого метода.

4. Сравните полученные результаты, сделайте выводы

Решение:

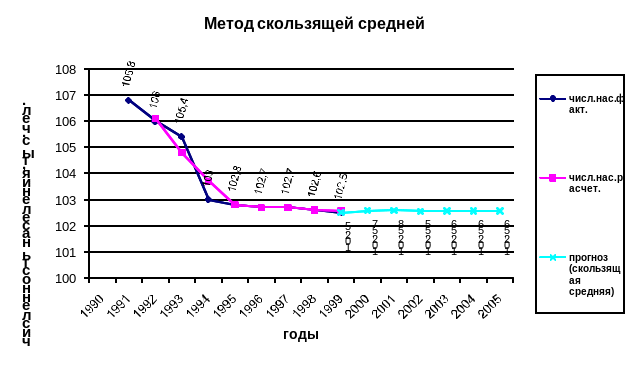
Метод скользящей средней.

Определим величину интервала сглаживания, например равную 3 (n=3).

Годы	Численность населения города, тыс. чел. y1	Скользящая средняя M	Расчет средней относительной ошибки |y1-m|*100 Y1
2003	106,8	-	-
2004	106	106,07	0,07
2005	105,4	104,8	0,57
2006	103	103,73	0,71
2007	102,8	102,83	0,03
2008	102,7	102,73	0,03
2009	102,7	102,67	0,03
2010	102,6	102,6	0,0
2011	102,5	102,56
Итого	934,5		1,44
Прогноз
2012	102,57
2013	102,58

Рассчитаем скользящую среднюю для первых двух периодов.

M₂₀₀₄=(y₂₀₀₃+y₂₀₀₄+y₂₀₀₅):3= (106,8+106,0+105,4):3=106,07

М₂₀₀₅=(y₂₀₀₄+y₂₀₀₅+y₂₀₀₆):3=(106,0+105,4+103,0):3=104,8

Рассчитав скользящую среднюю для всех периодов, строим прогноз на 2012-2013 г.

y₂₀₁₂=102,6+1/3*(102,5-102,6)=102,6-0,03=102,57

Определяем скользящую среднюю m для 2011 г.

m= (102,6+102,5+102,57):3=102,56

Строим прогноз на 2013 г.

y₂₀₁₃=102,56+1/3*(102,57-102,5)=102,58

Рассчитываем среднюю относительную ошибку:

є =1,44:7=0,21%

Вывод: По расчетам прогноза видно, что численность населения практически не меняется и составляет в среднем на 2012-102,57 тыс.чел.,а на 2013- 102,58 тыс.чел. Так как средняя относительная ошибка равна 0,21%, то точность данного прогноза является высокой.

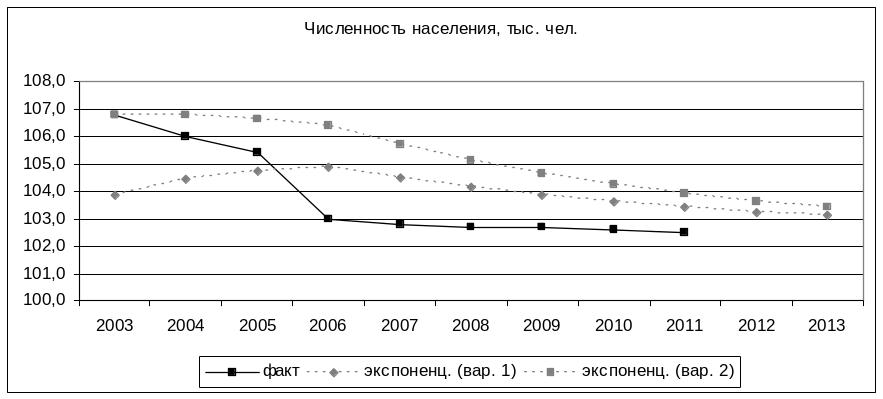
Метод экспоненциального сглаживания.

Определяем значение параметра сглаживания:

α = 2/(n+1)=2/(9+1)=0,2

Определяем начальное значение U₀ двумя способами:

I способ (средняя арифметическая) U₀ =934,5 : 9=103,83;

II способ (принимаем первое значение базы прогноза) U₀ =106,8.

Рассчитываем экспоненциально взвешенную среднюю для каждого года, используя формулу

y_t+1= α  y_t+(1- α) U_t.

I способ: U₂₀₀₄ =106,8*0,2+(1-0,2)*103,83=104,42

U₂₀₀₅ =106*0,2+(1-0,2)*104,42=104,74

U₂₀₀₆ =105,4*0,2+(1-0,2)*104,74=104,87

U₂₀₀₇ =103*0,2+(1-0,2)*104,87=104,50

U₂₀₀₈ =102,8*0,2+(1-0,2)*104,5=104,16

U₂₀₀₉ =102,7*0,2+(1-0,2)*104,16=103,87

U₂₀₁₀ =102,7*0,2+(1-0,2)*103,87=103,64

U₂₀₁₁ =102,6*0,2+(1-0,2)*103,64=103,43

Составим таблицу.

Годы	Численность населения города, тыс. чел. Y1	Экспоненциально взвешенная средняя Ut		Расчет средней относительной ошибки
		I Способ	II Способ	I Способ	II Способ
2003	106,8	103,8	106,8	2,81	0,0
2004	106	104,42	106,8	1,49	0,75
2005	105,4	104,74	106,64	0,63	1,18
2006	103	104,87	106,39	1,82	3,29
2007	102,8	104,5	105,71	1,65	2,83
2008	102,7	104,16	105,13	1,42	2,37
2009	102,7	103,87	104,64	1,14	1,89
2010	102,6	103,64	104,25	1,01	1,61
2011	102,5	103,43	103,92	0,91	1,39
Итого	934,5	937,43	949,75	12,88	15,31
Прогноз
2012		103,24	103,64
2013		103,09	103,41

II способ: U₂₀₀₄ =106,8*0,2+(1-,02)*106,8=106,8

U₂₀₀₅=106*0,2+(1-,02)*106,8=106,64

U₂₀₀₆ =105,4*0,2+(1-,02)*106,64=106,39

U₂₀₀₇ =103*0,2+(1-,02)*106,39=105,71

U₂₀₀₈ =102,8*0,2+(1-,02)*105,71=105,13

U₂₀₀₉ =102,7*0,2+(1-,02)*105,13=104,64

U₂₀₁₀ =102,7*0,2+(1-,02)*104,64=104,25

U₂₀₁₁ =102,6*0,2+(1-,02)*104,25=103,92

Рассчитываем прогнозное значение, используя формулу :

y_t+1= α  y₂₀₁₁+(1- α) U_t.

I способ: U₂₀₁₂=102,5*0,2+0,8*103,43=103,24

U₂₀₁₃=102,5*0,2+0,8*103,24=103,09

II способ: U₂₀₁₂=102,5*0,2+0,8*103,92=103,64

U₂₀₁₃=102,5*0,2+0,8*103,64=103,41

Средняя относительная ошибка :

є

I способ: є =12,88:9=1,43% II способ: є =15,31:9=1,7%

Вывод: По рассчитанной средней относительной ошибке видно, что наиболее точность прогноза по методу экспоненциальной взвешенной наблюдается в первом способе расчета (є=1,43), т.е. по средней арифметической.