Лабораторная работа 7. Многомерное шкалирование

Цель: привитие навыков визуализации взаимосвязи объектов в метрическом пространстве с последующим их дескриптивным описанием.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Цель многомерного шкалирования – выявить структуру исследуемого множества объектов, выделив набор потенциальных переменных, по которым различаются объекты, и описать каждый объект в терминах этих переменных.

В качестве средства решения используется геометрическое представление объектов в виде точек пространства небольшого числа измерений. Необходимо построить пространство и расположить в нем точки-объекты так, чтобы расстояния между ними наилучшим образом (в смысле некоторого критерия) соответствовали заданным различиям.

Формальная постановка задачи шкалирования выглядит следующим образом. По исходной матрице попарных различий G построить координатное пространство возможно меньшей размерности r и найти в нем координаты точек-объектов так, чтобы матрица расстояний D между ними, вычисленная по введенной на Х метрике, была, в смысле некоторого критерия, близка к исходной матрице G:

, , .

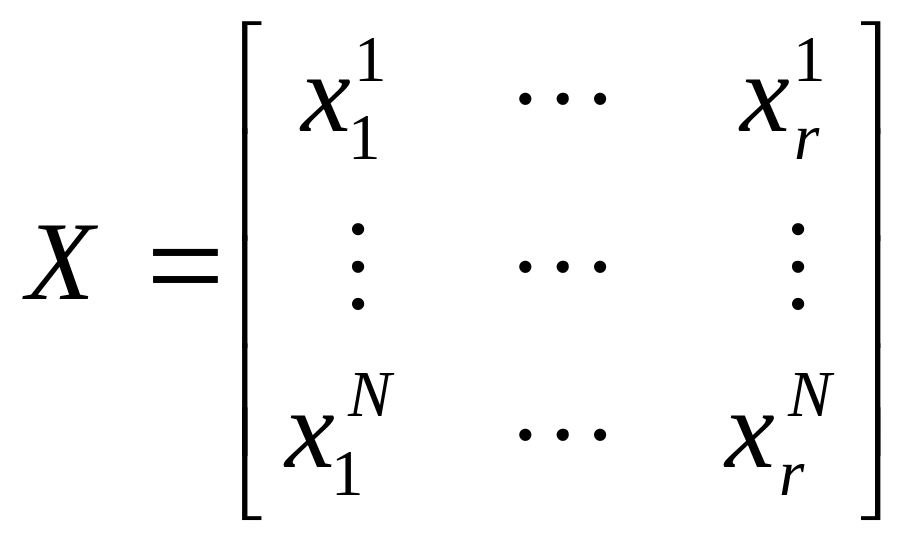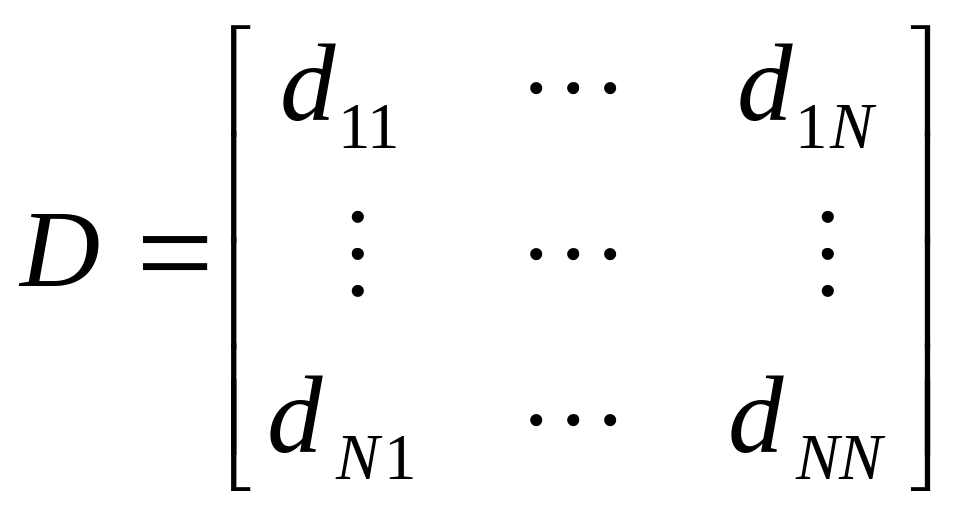Различают метрическое и неметрическое шкалирование. В метрическом шкалировании матрица различий G удовлетворяет аксиомам метрики, то есть является матрицей расстояний, тогда как в неметрическом – этого не требуется. Здесь необходимо обеспечить соответствие порядка расстояний порядку различий:

→ .

Решение задачи многомерного метрического шкалирования проводят по методу Торгерсона, опирающегося на теорему Янга-Хаусхолдера. Для неметрического шкалирования широкое распространение получил алгоритм Краскала.

В методе главных проекций Торгерсона предполагается, что матрица G – матрица евклидовых расстояний между объектами, не содержащая ошибок. По матрице G вычисляют симметричную матрицу B_i размерности NхN с элементами b_jk , представляющими скалярное произведение векторов с началом в точке i и концами в точках j и k:

.

Любая из N точек может быть взята в качестве i-й. Таким образом можно получить N возможных матриц B_i. Согласно теореме Янга-Хаусхолдера:

1. Если какая-либо B_i (i=1,2,…,n) является положительно полуопределенной (ППО), то различия между объектами можно рассматривать как расстояния между точками в вещественном евклидовом пространстве.

2. Ранг любой ППО матрицы соответствует размерности r множества точек. (Напомним, то ранг ППО матрицы равен числу положительных собственных значений).

3. Любую ППО матрицу можно факторизовать в виде B_i = XX’. Элементы Х есть проекции точек-объектов на r ортогональных осей в r-мерном вещественном пространстве с центром в точке i.

Рассмотрим один из известных алгоритмов неметрического многомерного шкалирования, предложенный Дж. Краскалом.

Пусть – оценки координат, где i – номер точки; k – номер координаты; – оценка расстояний по -метрике; – ранговые образы расстояний, иначе отклонения. Эти величины должны соответствовать, насколько это возможно, оценкам расстояний, но с сохранением условия монотонности:

.

Для оценки степени расхождения вводят меру соответствия (S-стресс):

либо ,

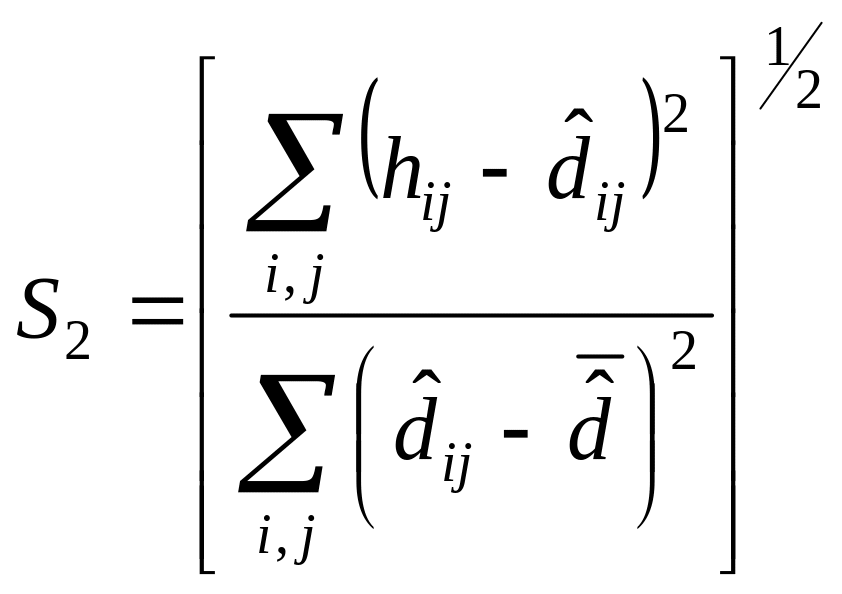где – среднее арифметическое оцененных расстояний.

Наряду с S-стрессом используется SS-стресс, где в числителе оценки расстояний и отклонения заменены их квадратами. SS-стресс обеспечивает более быструю сходимость, если матрица различий симметрична.

Алгоритм Краскала состоит из пяти основных этапов:

1. Формирование стартовой конфигурации, то есть получение начальных оценок координат (размерность пространства предполагается известной);

2. Стандартизация расстояний и оценок координат;

3. Неметрический этап, в ходе которого вычисляются отклонения;

4. Метрический этап: перерасчет оценок координат.

5. Подсчет меры соответствия.

Если мера улучшилась, то возвращаются к этапу 2; в противном случае – работа алгоритма завершается.

Для текущей конфигурации точек можно построить график зависимости воспроизведенных расстояний от исходных расстояний. Такая диаграмма рассеяния называется диаграммой Шепарда. По оси ординат откладываются воспроизведенные расстояния, а по оси абсцисс — исходные расстояния между объектами. На этом графике также строится график ступенчатой функции. Ее линия представляет собой результат монотонного преобразования исходных данных. Если бы все воспроизведенные расстояния легли бы на эту ступенчатую линию, то ранги наблюдаемых расстояний был бы в точности воспроизведен полученным решением (пространственной моделью). Отклонения от этой линии показывают на ухудшение качества согласия (т. е. качества подгонки модели).

Чем больше размерность r пространства, тем точнее можно воспроизвести исходную матрицу расстояний, однако практический интерес представляют пространства невысокой размерности, поскольку упрощается визуальный анализ получающейся конфигурации точек и интерпретация латентных переменных.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. В чем состоит цель многомерного шкалирования ?

2. Каким условиям должна удовлетворять матрица различий в метрическом шкалировании?

3. В чем состоит теорема Янга-Хаусхолдера?

4. Что показывает диаграмма Шепарда?

5. Как подбирается размерность r метрического пространства?

6. Чем SS—стрессы отличаются от S-стресса?

ЗАДАНИЕ

1. Подготовить исходные данные (по указанию преподавателя).

2. Освоить работу с модулем «Многомерное шкалирование».

в пакете STATISTICA

3. Проинтерпретировать полученные результаты

Модуль «Многомерное шкалирование» пакета Statistica поддерживает только формат данных в виде матриц. К ним относятся как симметричные, так и треугольные матрицы. Для того чтобы файл входных данных был распознан как файл матрицы, он должен удовлетворять следующим условиям:

• Число строк = число столбцов + 4.

• Матрица должна быть квадратной, а названия строк и столбцов должны совпадать.

• Последние 4 строки содержат следующие сведения:

Means. В этой строке показано среднее арифметическое всех значений конкретного столбца. Для матриц сходств и различий эта строка может быть пустой.

St.Dev. В этой строке показана дисперсия значений конкретного столбца. Для матриц сходств и различий эта строка может быть пустой.

No.Cases.В этой строке задано число строк данной матрицы.(Обязательный параметр.)

Matrix.Данный параметр определяет тип используемой матрицы;

1-корреляционная матрица;

2-матрица сходств;

3-матрица различий;

4-ковариационная матрица.

(Обязательный параметр.)

Корреляционная матрица (Matrix=1). Корреляционные матрицы можно создать, например, с помощью команды Save correlation Matrix в модуле Multiple Regression-Reviewing Descriptive Statisics. Корреляционную матрицу можно также создать вручную, задав корреляции в обычной таблице и включив в файл последние четыре строки, описывающие матрицу.

Матрица сходств (Matrix=2). В этой матрице выражены сходства между объектами (переменными). Этот тип файла матрицы можно импортировать либо создать вручную, задав в обычнй таблице и включив в файл последние четыре строки, описывающие матрицу.

Матрица различий (Matrix=3). Эту матрицу можно создать вручную либо использовать команду Save distance matrix модуля Cluster Analysis - Joining Results.

Ковариационная матрица (Matrix=4). Квадратные ковариационные матрицы содержат коэффициенты ковариации для всех пар указанных переменных. На диагонали при этом находятся дисперсии для каждой переменной. Ковариационные матрицы могут быть созданы вручную путем ввода коэффициентов ковариации в обычную таблицу и добавления в нее последних четырех строк, описывающих тип матрицы.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА [4, 12, 14]