5.19 Опишите назначение процедуры стратификации данных (5 баллов). Определите понятие «диаграмма рассеивания» и проанализируйте ее наиболее характерные виды (15 баллов ).

Назначение процедуры стратификации данных:

Одним из наиболее простых статистических методов является метод расслоения (стратификации) данных. В соответствии с этим методом производят расслоение данных, то есть группируют данные в зависимости от условий их получения и производят обработку каждой группы в отдельности.

При расслоении данных следует стремиться к тому, чтобы различие внутри группы было как можно меньше, а различие между группами – как можно больше.

Расслоение позволяет получить представление о скрытых причинах дефектов, а также помогает выявить причину появления дефекта, если обнаруживается разница в данных между «слоями». Например, если расслоение проведено по фактору «исполнитель», то при значительном различии в данных можно определить влияние того или иного исполнителя на качество изделия; если расслоение проведено по фактору «оборудование» – влияние использования разного оборудования.

Если после расслоения данных невозможно определить наглядно решающий фактор в решении проблемы, то необходимо проводить более глубокий анализ данных.

На практике стратификация используется для расслаивания статистических данных по различным признакам и анализа выявленной при этом разницы  в диаграммах Парето, схемах Исикавы, гистограммах, диаграммах рассеивания и т.д.

«Диаг-ма рассеив-ия» и анализ ее наиболее хар-ых видов:

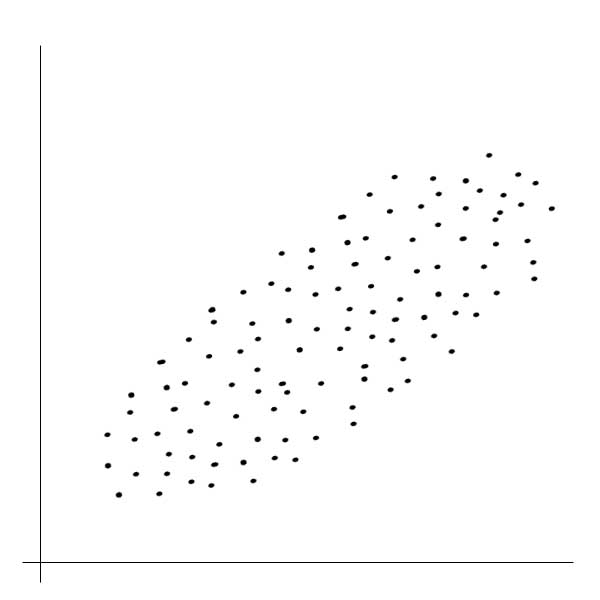
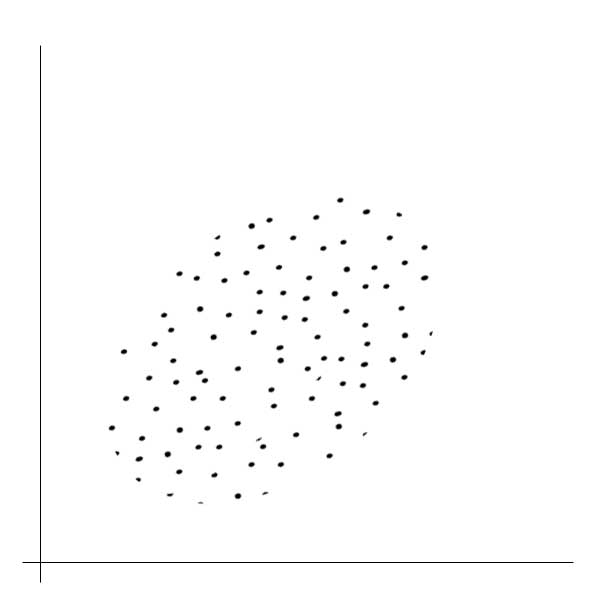
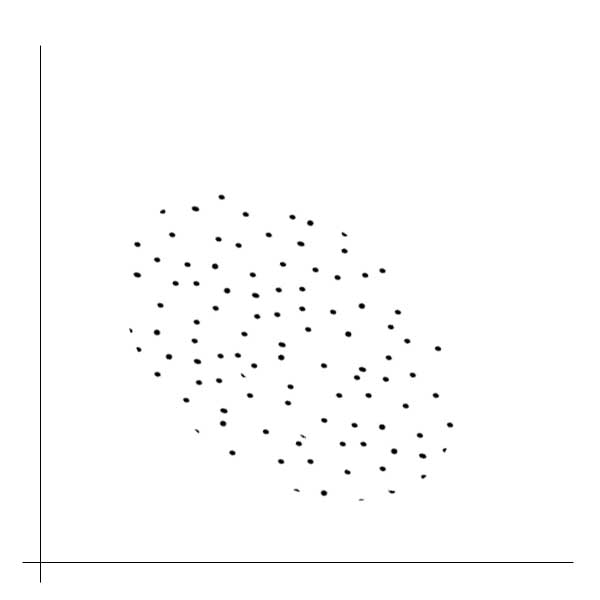
Диаграмма рассеяния (разброса) применяется, когда требуется выяснить наличие линейной связи между двумя контролируемыми параметрами. То есть выяснить, как будет изменяться одна переменная величина при изменении значений другой. Диаграмма рассеяния в то же время не показывает, какая переменная является причиной, а какая следствием. То есть диаграмма рассеяния отражает не только наличие линейной связи, но и тесноту этой связи. Диаграмма рассеяния строится в следующем порядке: по горизонтальной оси откладываются измерения величин одной переменной, а по вертикальной оси - другой переменной. На самом поле диаграммы отмечается точка, координаты которой соответствуют значениям первой и второй переменной. Диаграммы рассеяния представляют собой некоторую совокупность точек на графике. - Если совокупность точек группируется около прямой под углом 45 градусов, то это означает наличие положительной связи между этими переменными. То есть, увеличение значений одной переменной сопровождается ростом значений другой переменной. - Если совокупность точек группируется около прямой под углом 135 градусов, то это означает наличие отрицательной связи между этими переменными. То есть, увеличение значения одной переменной приводит к уменьшению значений другой переменной. - Если же точки на этой диаграмме расположены хаотически, то это означает отсутствие линейной связи между анализируемыми переменными.

- Если совокупность точек группируется в виде окружности, то связь отсутствует (равна 0).

сильная прямая зависимость

сильная обратная зависимость слабая прямая зависимость слабая прямая зависимость