Примеры распр-ий дсв и нсв, исп-ых в упр-нии кач-ом:

1. Распределение дсв

1. Биноминальное распределение - Базируется на последовательности испытаний Бернулли, состоящем в n идентичных испытаний, удовлетворяющих следующим условиям:

• Каждое испытание имеет 2 исхода (успех/не успех)

• Вероятность успеха испытания =p, не успеха q=1-р

• Все испытания независимы

ДСВ, для которой вычисляется число успехов в n повторяемых испытаний, подчиняется биноминальному закону распределения с параметрами n и p.

Вероятность того, что число успешных испытаний будет равна m, вычисляется по формуле:

где n – число исп-ий; m – число успешных исп-ий; p – вероятность успешного исп-ия

Хар-ки распределения:

; ;

2. Распределение Пуассона - закон распределения ДСВ является частным случаем биноминального распределения и используется для редких событий.

где:  - параметр распределения Пуассона; =np; e=2,71; n-число независ. испытаний с вероятность р; m-число положительных испытаний.

Св-во распределения:

2. Распределение нсв

1. Нормальный (Гаусса) закон распределения

СВ имеет НЗР ф-ции плотности вероятности, если её ф-ция плотности вероятности имеет вид:

, где

 = 3,14; exp=е=2,71; ;

Свойства:

• Функция существует при любых х

• Функция принимает только положит-ые значения

• При неогранич-ых возрастаниях

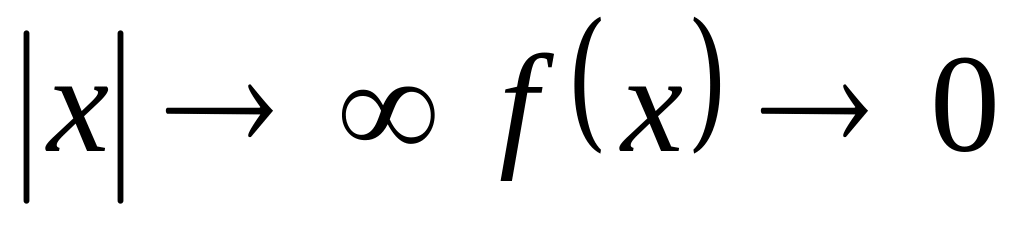
• f(x) принимает максимальное значение при x=a:

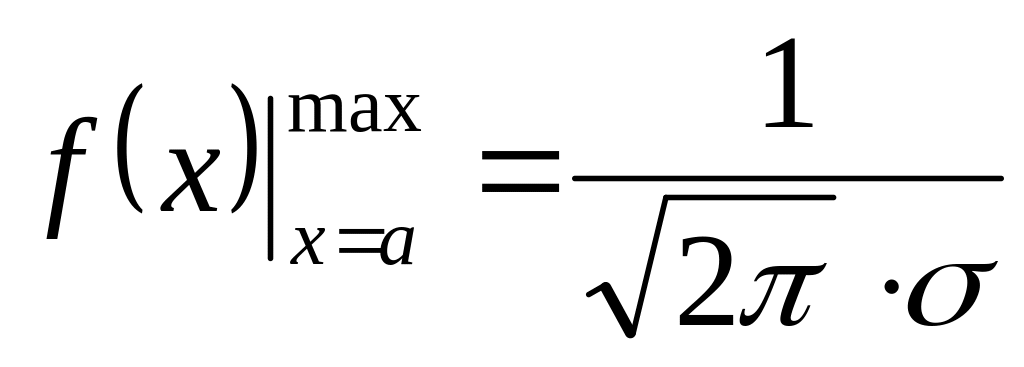
• Распределение симметрично относительно x = a

• Распределение имеет 2 точки перегиба относительного математического ожидания

2. Экспоненциальное распределение

Оно является предельным переходом распределения Пуассона ДСВ. Оно описывает вер-ть временного интервала до момента появления редкого события, подчиняющегося з-ну Пуассона.

Например: велечину временного интервала до возникновения первого отказа в работе оборудования.

Экспоненциальное распределение задается ур-ем вида:

, где  - интенс-ть распр-ия

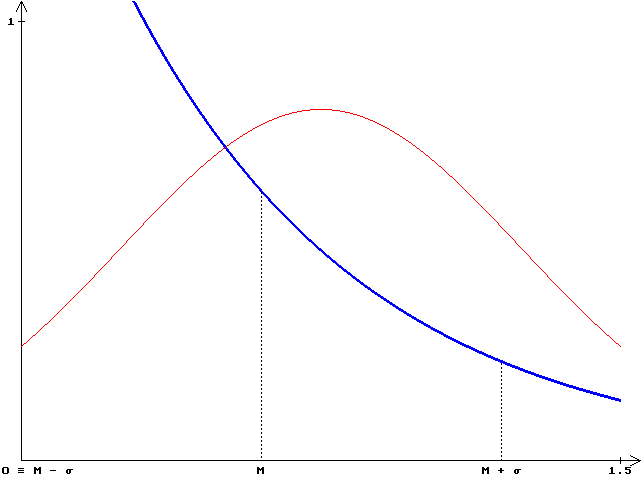
Интегральная функция распределения:

Свойства:

• Математическое ожидание

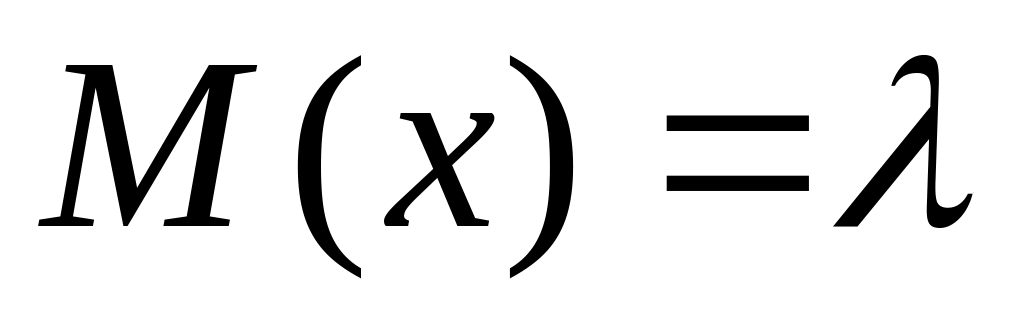
• Дисперсия

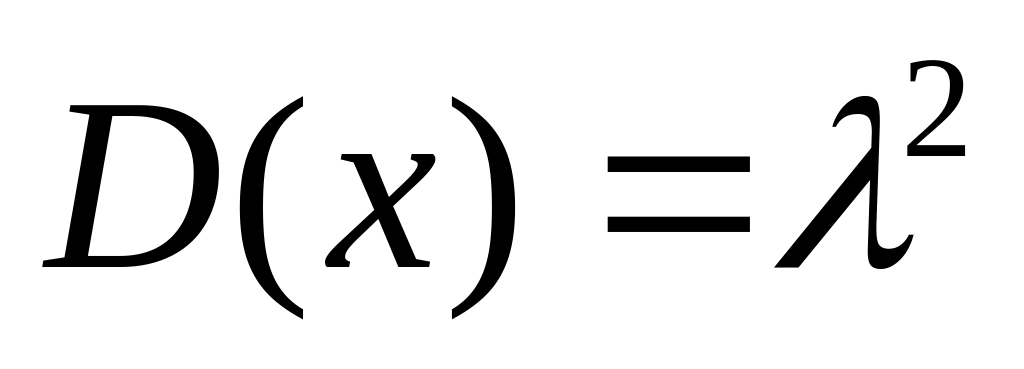
3. Закон равномерного распределения

Если известно, что возможные значения НСВ принадлежат опред-ному интервалу, а вер-ти принятия любого знач-я в этом интервале примерно одинаковы, то считается, что данная НСВ имеет равном-ный з-н распред-ния.

, где с – верхняя горизонтальная граница прямоугольника (по оси у)

Св-ва распределения:

1)

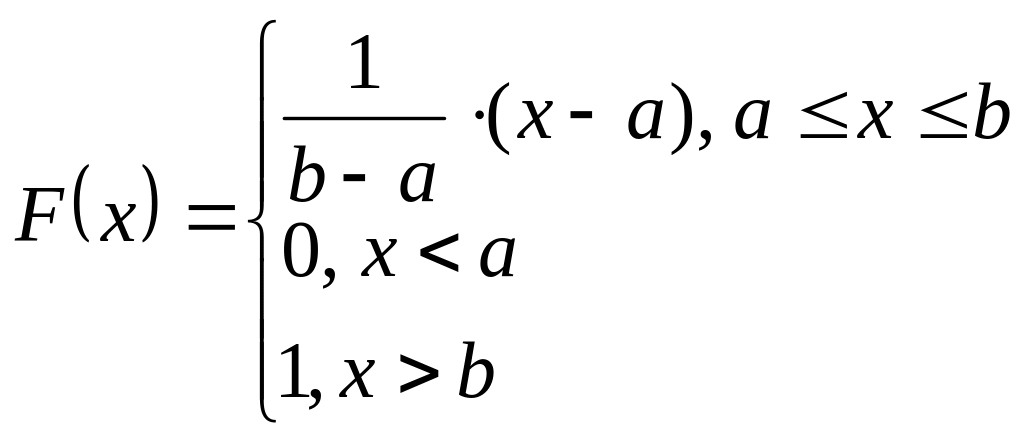
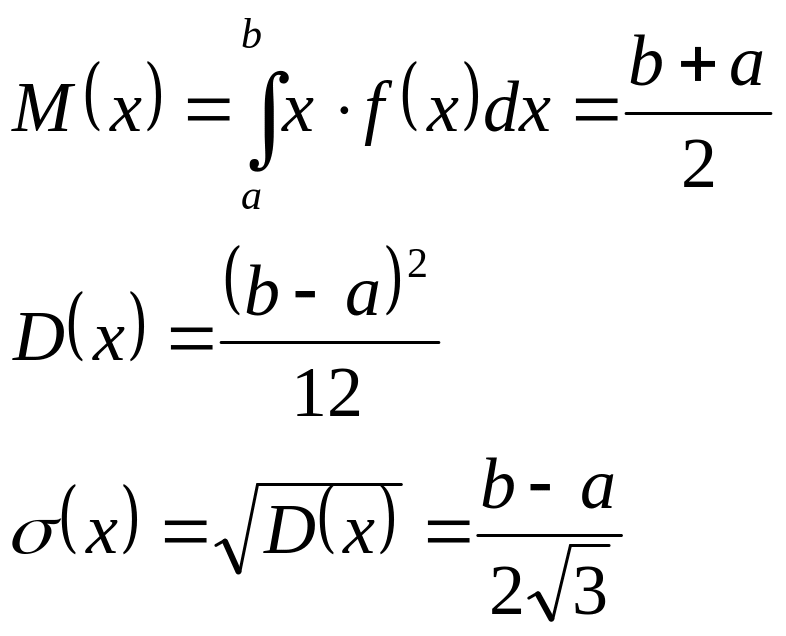
Оцените вероятность попадания непрерывной СВ в интервал : ± σ; ± 2σ; ± 3σ; относительно её математического ожидания

Правило 3σ:Вероятность того, что отклонение СВ х, имеющей нормальное распределение, будет отклоняться от математического ожидания по абсолютной величине не более, чем на , равняется:

Если обозначить , то получ-ся, что ;

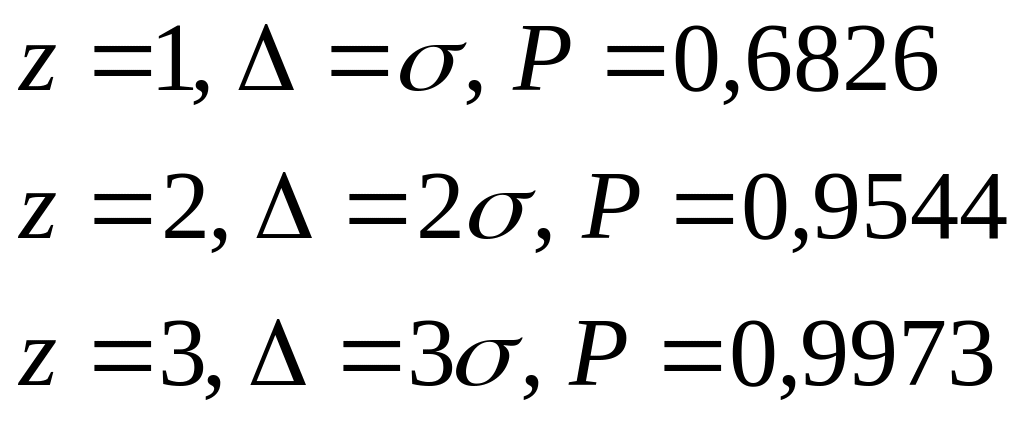
5.9 Определите количество процентов площади под кривой нормального распределения, которое попадает внутрь диапазона: ± σ; ± 2σ; ± 3σ относительно её среднего (15 баллов). Укажите соответствующее этому число бракованных изделий на 1000 изделий (5 баллов).

Правило 3σ: Вероятность того, что отклонение СВ х, имеющей нормальное распределение, будет отклоняться от математического ожидания по абсолютной величине не более, чем на , равняется:

Если обозначить , то получ-ся, что ;

При Z = 1 внутрь диапазона под кривой нормального распределения попадает 68,3 % (Р = 0,6826).

При Z = 2 -/- 95,4 % (Р = 0,9544).

При Z = 3 -/- 99,7 % (Р = 0,9973).

Соотв-ее этому число бракованных изделий на 1000 изделий:

Из вышесказанного можно сделать вывод, что:

Вероятность того, что СВ с нормальным распределением отклонения от математич-ого ожидания на величину 3сигма очень мала и составляет

т.е на 1000 изделий возможно только 2,7 бракованных изделия. Число бракованных изделий при σ равно 317,4 из 1000, а при 2σ равно 45,6 из 1000.

5.10. Приведите основное уравнение теории надежности. Дайте стат. интерпретацию интенсивности отказов и укажите связь со средним временем безотказной работы (15). Укажите, как изменится надежность системы при последовательном и параллельном соединении одинаковых звеньев (5 баллов).

Основное ур-ие теории над-ти. Стат. интерпретация интенс-ти отказов, связь со средним временем безотк-ой работы:

Под над-ю понимается хар-ка готовности прод-ции к прим-ию, безотказность ее в работе и возможность обеспечения технического обслуживания (ТО) и технического ремонта (ТР).

При анализе надежности используются термины:

• Отказ – событие, после которого изделие перестает выполнять свои функции.

• Дефект – не вып-ие треб-ия, связ-го с предполаг-ым /уст-ым исп-ием, но не влияющего на выполнение функции.

• Соответствие – это выполнение треб-ия.

Для колич-ой оценки надежности исп-ся показатели:

• Вероятность безотказной работы P(t);

• Вероятность отказа Q(t);

• Интенсивность отказов λ(t);

• Среднее время безотказной работы (среднее время наработки на отказ) T_б;

• Гарантийный срок службы T_г.

Хар-ка над-ти –вероятностная хар-ка, подвергаемая стат. обр-ке.

Для получения стат. хар-к и закономерностей в качестве колич-ной меры надежности исп-ся вер-ть безотказной работы (это степень объективной уверенности безотказной работы объекта):

,где - зад-ое время работы до отказа; - время

Обр-ая вел-на (вер-ть отказа): ;

Исчерпывающей хар-кой времени безотказной работы является ф-ция распределения или функция ненадежности. Но чаще всего используется функция плотности распределения времени безотказной работы:

Вероятность появления отказа на интервале с началом t=0 определяется из соотношения:

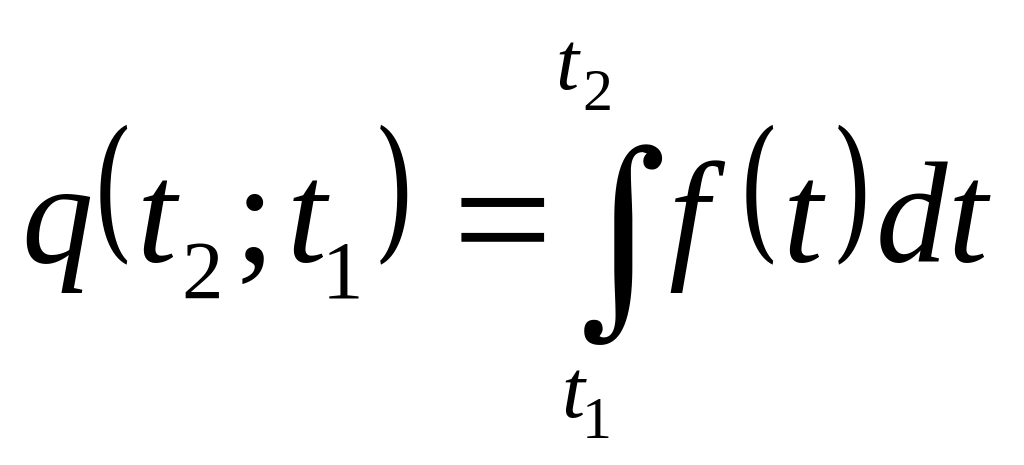
Вероятность безотказной работы определяется из соотношения:

Вводится понятие «вероятность безотказной работы» при условии безотказной работы на безотказном элементарном участке Δt:

Если Δt → 0 в предельном переходе получаем величину «интенсивность отказов»:

С помощью функции можно определить вероятность безотказной работы на интервале :

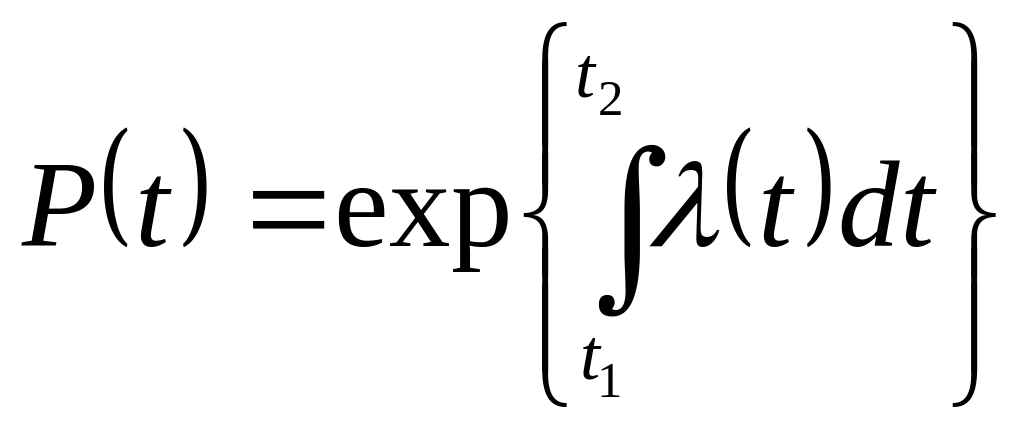
На интервале гарантийного срока службы T_г вып-ся усл-ие:

Средняя интенсивность отказов имеет связь со средним временем безотказной работы T_б по формуле:

Как изменится над-ть сист-мы при послед-ом и пар-ом соед-ии одинаковых звеньев:

1. Послед-ое соединение одинаковых звеньев в систему.

Вероятность безотказной работы системы обеспечивается при безотказной работе каждого одинакового звена (элемента).

Если функция плотности вероятности каждого элемента подчиняется экспоненциальному закону, то:

Вероятность отказа однотипного элемента определяется как:

Вероятность отказа системы определяется из формулы:

Если в системе только 2 однотипных элемента, то применяются формулы:

2. Параллельное соединение одинаковых звеньев с систему.

Отказ системы происходит в случае отказа всех элементов. Вероятность отказа системы опред-ся из формулы:

Вероятность безотказной работы однотипного элемента определяется как:

Вероятность безотказной работы системы определяется из формулы:

Если в системе только 2 однотипных элемента, то применяются формулы:

5.11. Сравните м/у собой сплошной и выборочный контроль (5). Изобразите функции плотности вероятности нормального распределения среднеарифметических значений для двух выборок, отличающихся по объему в четыре раза (15 баллов)

Сравните м/у собой сплошной и выборочный контроль:

Контроль качества продукции может быть сплошным и выборочным.

Сплошной контроль производится для всех значений в совокупности. Он требует больших затрат, в том числе и человеческих. С одной стороны он гарантирует с большей долей вероятности возможность обнаружения брака, но при этом надо учитывать и возможность ошибки от человеческого фактора. Сплошной контроль рекомендуется проводить при условии, когда это экономически выгодно и технически осуществимо. Спл. контроль не исключает ошибок, т.е. не дает полной гарантии.

Выб-ый контроль наоборот осущ-ся путем выборки опред-го числа изделий или значений из генеральной совокупности. Он требует меньших затрат, но вероятность обнаружения брака здесь ниже по сравнению со сплошным контролем. Однако виды контроля определяются условиями договора, условиями работы, треб-иями регламентов, стандартов и т.п. Проводят, когда при контроле продукция теряет качества или когда спл. контроль не выгоден или не осуществим.

Изобразите ф-ции пл-ти вер-ти норм-го распр-ия среднеарифм-их знач-ий для 2х выборок, отлич-ся по объему в 4 раза

Согласно центральной предельной теореме:

Среднее арифметическое из ряда измерений всегда имеет меньший разброс, чем разброс каждого определенного измерения. Из этого следует, что если необходимо повысить точность рез-та в 2 раза, то число измерений надо увеличить в 4 раза.

Для исходной выборки (объем в 4 р. меньше) будет один разброс среднеарифм-го знач-ия и разброс знач-ий .

Выборка, V кот-ой увеличен в 4 раза, будет разброс среднеарифм-го знач-ия в 2 раза меньше по ср-ию с первым (исходным). Увеличивая объем выборки уменьшается степень разброса.