5.1 Перечислите и дайте краткую хар-ку стат. методам, приведенным в стандарте ISO/TR 10017:2001 «Руководящ. указ-я по применению стат. методов при внедрении станд-та ИСО 9001:2000» (15 баллов). Дайте опр-ние термина «статистич-кое упр-ние процессом» (5 баллов).

• описательная статистика

Основывается на аналитических процедурах, этапных с обработкой и представлением колич-ых данных. Цель - колич-ая оценка хар-к полученных данных.

Возможными оценками полученных данных явл-ся: центральное значение (сред. знач., мода или медиана) и их разброс или рассеивание (диапазоном изменений, стандартное отклонение, дисперсия). Другой важной хар-ой является распределение данных.

Инф-ция м.б. изображена при помощи разнообразных графических методов. Графические методы позволяют выявить специфическое поведение данных, которое трудно обнаружить в рез-те колич-ого анализа.

Опис. стат-ку исп-ют для обобщения и описания групп данных. Обычно прим-ют на начальном этапе колич-го анализа данных, что пом-ет в выборе послед-их статист. процедур.

• планирование экспериментов

Планирование экспериментов представляет собой проведение специально спланированных исследований, опирающихся на статистическую обработку данных для получения результатов с определенным уровнем доверия.

Планирование осущ-ся с целью определения условий, при которых должны выполняться эксперименты.

Исп-ся для оценки основных признаков или хар-к прод-ции, процесса или системы с определенным уровнем доверия. Данные затем могут быть исп-ны для проверки их соотв-ия опред-му стандарту или сравнительной оценки нескольких систем.

• проверка гипотез

Проверка гипотез является стат. процедурой для проверки обоснованности гипотезы, рассматривающей параметры одной пли нескольких выборок с определенным уровнем доверия. Это может помочь в принятии решений, зависящих от выбранных параметров.

Распространение данного статистического метода объяснялся тем, что он может быть использован для описания «доверительного интервала», в который может попасть параметр с определенным уровнем доверия.

Проверка гипотезы непосредственно или косвенно используется вместе с некоторыми статистическими методами, в отчетах таких как выборочный контроль, контрольные карты, планирование экспериментов, регрессионный анализ и другие.

• анализ измерений

Анализ измерений представляет собой набор процедур для оценки точности измерительной системы в условиях ее работы.

Используется для проверки с определенным уровнем доверия пригодности измерительной системы для достижения поставленных целей. Обеспечивает недорогой и эффективный способ выбора измерительных приборов или принятия решения о возможности использования прибора для оценки контролируемого параметра продукции или процесса.

• анализ возможностей процессов

С помощью анализа возможностей процесса осуществляется проверка изменчивости процесса и оценка доли несоответствующей продукции. Это позволяет поставщику оценить издержки, от несоответствий и помогает принять решения по улучшению процесса. Понятие возможностей процесса применяется только к стабильному процессу. Анализ возможностей процесса должен использоваться совместно с методами управления для обеспечения объективности результатов управления.

• регрессионный анализ

Регрессионный анализ связывает поведение изучаемой характеристики («переменной отклика») с потенциальными причинами («переменными причин»). Целью регрессионного анализа является помощь при выявлении причины вариации отклика и определении влияния каждой возможной причины на подобную вариацию. Это достигается путем статистической связи вариации в переменной отклика с вариацией в переменных причин. Обеспечивает понимание связи между различными факторами и ожидаем им откликом, что помогает в принятии решений, связанных с изучаемым процессом, и в конечном счетё улучшает процесс.

• анализ надежности

Анализ надежности является примером использования инженерных и аналитических методов для решения проблем надежности. Анализ надежности используется для: 1.прогноза результатов событий (или отказов);2.моделирования схем отказов и управления выпускаемой продукцией или предоставляемыми услугами; 3. определения частоты случайных событий.

• выборочный контроль

Выборочный контроль является систематическим статистическим методом для получения информации о характеристиках совокупностей путем изучения представительной выборки этой совокупности. Применяемыми методами выборочного контроля могут быть простой, случайный, систематический, последовательный и другие методы. Выборочный контроль может быть разделен на две обширных, взаимосвязанных друг с другом области: «статистический приемочный контроль» и «выборочное обследование». Статистический приемочный контроль обеспечивает принятие решений относительно приемлемости или неприемлемости партии по результатам выборки, сделанной из этой партии. Выборочное обследование используется при аналитических исследованиях с целью оценки значений одной или нескольких характеристик совокупности или получения распределения этих характеристик.

• моделирование

Моделированием называется совокупность процедур, с помощью которых теоретическая или эмпирическая система может быть представлена математически в виде компьютерной программы для поиска решения проблемы. Преимуществом моделирования является получение решения для любого случая с экономией времени и средств.

• контрольные карты

Карта статистического управления процессом или контрольная карта является графическим Представлением данных из выборки, которые периодически берутся из процесса и наносятся на график в соответствии со временем. Кроме того, на контрольных картах отмечаются «контрольные границы», которые описывают присущую изменчивость устойчивого процесса. Целью контрольной карты является помощь в оценке стабильности процесса на основе изучения и нанесения на график данных с учетом контрольных границ.

• построение доверительных интервалов

Построение доверительных интервалов представляет процедуру определения допусков, основанную на достоверности действий, совершенней с помощью статистического распределения измерений.

• анализ временных рядов

Анализ временных рядов применяется для описания поведения моделей во времени и определения применимости данных для точного прогнозирования изменений. Кроме того, он и пользуется для выявления неожиданного изменения формы временного ряда. Полезен в планировании, конструировании, определении изменений процесса, а также измерении эффекта определенного внешнего вмешательства или действия.

Стат. упр-ие процессами – это основанноеое на стат. мышлении использование как стат., так и нестат. методов анализа и решения проблем с целью осуществления действий, необходимых для достижения и поддержания состояния стат. управляемости процессов, и постоянного улучшения их стабильности и воспроизводимости.

Стат. мышление – основанный на теории вариабельности способ принятия решений о том, надо или не надо вмешиваться в процесс, и если надо, то на каком уровне.

Стат. упр-ие процессами – прежде всего, ср-во понимания вариабельности проц-ов и путей её уменьш-я.

5.2 Проанализ-те взаимосвязь м/у стат. методами упр-ния кач-вом прод-ции и семью этапами цикла управления по К.Исикава (5 баллов). Опр-те различия и взаимосвязь м/у допусковым и стат. подходами к контролю кач-ва (15 баллов).

Цикл упр-ия кач-ом предст-ет собой виток спирали и в соотв-ии с предлож-ем Исикавы он должен состоять из 7 этапов:

1 этап - Поиск проблемы: Цель – осознать проблему, показать её важность, определить цель исследования.

• Показать истоки проблемы

• Выбрать для решения наиболее важную проблему

• Продемонстрировать потери, связанные с этой проблемой (выражать потери лучше в денежном эквиваленте)

• Назначить отв-го за решение проблемы

• Опр-ие бюджета для решения проблемы

• Составление плана для решения проблемы

 проблема должна быть не только актуальной, но и решаемая

в данных условиях 

2 этап – Наблюдение: Цель – обнаружить факторы, порождающие проблему. Для этого прводится:

• Исслед-ие обстоят-в (время, место, тип и признаки)

• Исслед-ие проблемы с разных точек зр-я (диагр. Исикавы)

• Сбор инф-ции в виде данных (контрольные листки)

3 этап- Анализ: Цель – опр-ие главных причин проблемы, выдвижение гипотез и их анализ.

• Предложение гипотез на основе диаг-мы Исикава

• Отброс малозначит. факт-ов на основе д-мы Парето

• Рассм-ие новой причинно-следственной диаграммы

• Выделение многозначительных факторов

• Составление новых планов и их анализ

• Стратификация (или расслоение) данных

4 этап-Разработка и выполнение мероприятий: Цель – определить действия, мероприятия, которые целесообразно выполнить при решении проблемы.

• Выделение и формулировка мероприятий по лечению и профилактики "проблемы"

• Нужно убедится, что мер-ие не порождает лишних проблем

• Взвешивание всех "+" и "-" каждого решения данной проблемы

• Орг-ия обучения персонала по выбранному решению

5 этап – Проверка: Цель – убедится в эфф-ти выбранных действий.

• Сравнение данных "до" и "после"

• Выражение рез-тов в денежной форме

• Привидение побочных рез-тов

• Построение диаграммы Парето "до" и "после"

6 этап – Стандартизация: Цель – разработка и внедрение системы действия против рецедивива проблемы.

• Формулировка и нахождение ответов на вопросы: что, где, когда, как и почему и как должен делать и оформление этих вопросов документально (СТП)

• Орг-ия подготовки персонала

• Устан-ие системы отв-ти и проверки соблюд-ия ст-та

7 этап- Окончание работы: Цель – анализ и оценка эфф-ти всех действий по решению данной проблемы и планирование дальнейших действий.

• Обобщение достигнутых рез-тов

• Оценка эфф-ти выбранных методик

• Составление перечня оставшихся проблем

• Составление плана работы

Различия и взаимосвязь м/у допусковым и стат. подходами к контролю кач-ва.

Допусковый подход по Тейлору предполагает, что есть номинальное значение и допустимые отклонения.

При допусковом контроле партия считается не принятой, если хотя бы одно из изделий выходит за пределы допуска и принимается, если все изделия находятся в пределах допуска. При стат. контроле учитывается разброс и распределение параметров.

Результаты контроля	Доп.	Стат.	Реш-е о действиях
	Да	Да	-
	Да	Нет	Рем-т, настр-ка оборуд-я
	Да	Да	Настр-ка оборуд-ия
	Нет	Да	Настр-ка оборуд-ия
	Нет	Да	Необх-мо устронить выброс
	Да	Нет	Необх-мо рассл-ие данных
	Нет	Нет	Необходим ремонт

Разница м/у ними: стат. методы позволяют выявить настроенность процесса, причины влияния, определить характер направленности действий. Неправильный выбор хар-ра возд-я приводит к потерям.

5.3 Укажите на сходство и различия м/у детерминированными и случайными данными (5 баллов). Объясните, что характеризует элементы описательной статистики: мода, медиана и среднеарифм. занчение случайной величины (15 баллов).

СВ – в теории вер-ей, величина, принимающая в зав-ти от случайного исхода испытаний те или иные значения с опред-ми вероятностями. Она может принимать бесконечную (непрерывная СВ) или конечную последовательность различных значений (дискретная СВ), при этом распределение вероятностей (закон распределения СВ) задается указанием этих значений и соответствующим им вероятностей их наступления.

Детерминированная величина (от лат. determino – определяю) – величина, принимает определенное (детерминирующее) значение или закономерно изменяется при повторных измерениях параметра. Эти величины (данные) выражают закономерную взаимосвязь и причинную обусловленность всех явлений.

Сходством данных величин является то, что они обе могут принимать значения, но СВ принимает те или иные значения с опред-ми вер-ми в зав-ти от случайного исхода испытаний, а детерминир-ая величина – закономерно обусловленное значение.

Объясните, что хар-ют эл-ты описат-ой стат.Ки: мода,

медиана и среднеарифметическое значение СВ:

Измеренные данные, обозначаются X_i ,какого-либо параметра представляют собой первичный статистический материал. Для того, чтобы эти рез-ты сделать обозримыми и удобными X_i ранжируют, т.е. располагают в определенной последовательности. Если некоторые X_i повторяются, то их объединяют, а число повторений обозначают m_i, которое называется абсолютной частотой или статистическим весом X_i. Такой ряд наз-ся статистич-ким рядом. Этот ряд принято характеризовать двумя выжнейшими показателями:

1) ср. положение измеренных значений

2) отклонение измеренных значений от среднего.

Для характеристики среднего положения X_i применяют: 1) ср. арифмети. знач-ие; 2)медиана; 3) мода.

Для простой стат-кой последовательности, где каждое X_i встречается однократно среднее арифметич. знач-ние определяют из условия: (n- число значений)

Для статистич-ого ряда САЗ вычисляется из условия:: 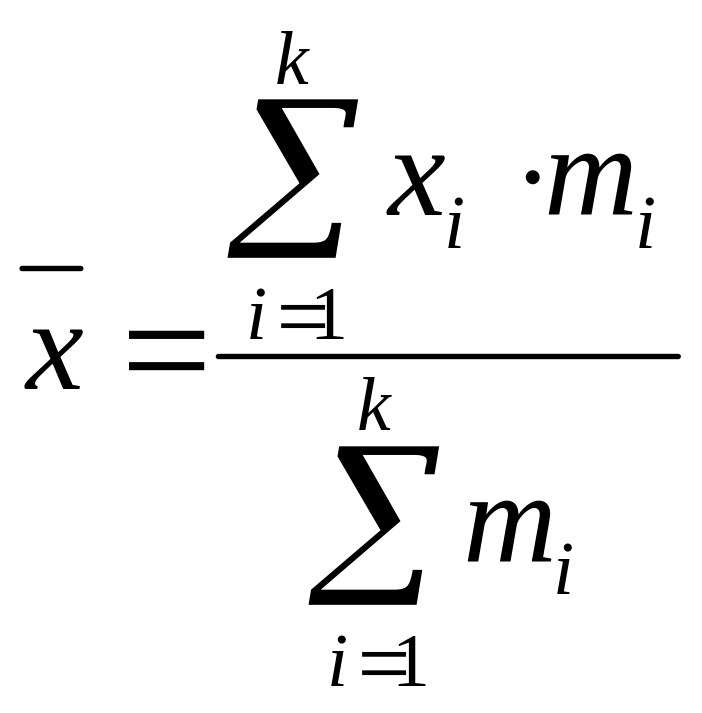, где k – число членов стат. ряда

Медиана ( ) делит упоряд-ый ряд значений X_i пополам на две равные части. Если общее число не четное, то медиана будет совпадать со средним членом ряда:

Если четное число членов, то равняется полусумме выборочных значений:

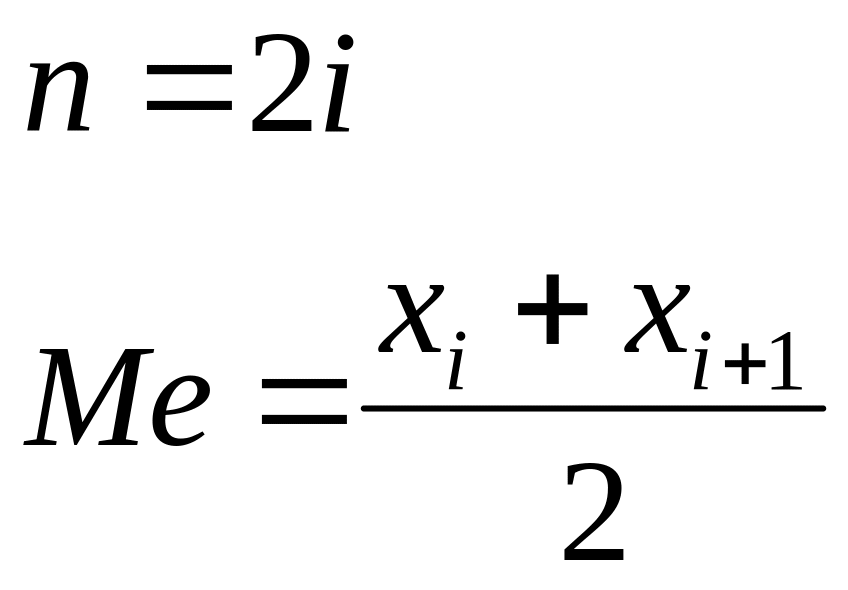
Значение требует мин-ых вычислений и ранжировки данных.

Выборочная мода – значение измеренных величин, которое наблюдается наиболее часто в стат. ряду.

Любая выборочная характеристика явл-ся случайной величиной.

Для симметричной статистической последовательности справедливо рав-во среднеарифм-го, медианы и моды.

5.4 Изобразите в системе координат график нормального (гауссова) распред-ния (5 баллов). Вычислите стандартное отклонение по набору данных из пяти единичных наблюдений: 1,5; 1,2; 1,1; 1,0; 1,6 (7 баллов). Сколько единиц стандартных отклонений надо отложить симметрично относительно среднего, чтобы охватить 40% площади под нормальной кривой? (8 баллов).

Изобразите в системе координат график нормального (гауссова) распределения:

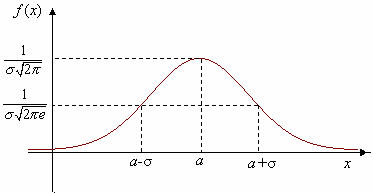
- Функция определена на любых действительных Х, т.е. от –бескон. до +бескон.

- всегда положительная

- если модуль Х стремится к бесконечности, то f(x) стремится к 0

- при Х=а, f(x)=max. значение

- симметрично относительно а

Вычислите стандартное отклонение по набору данных из пяти единичных наблюдений: 1,5; 1,2; 1,1; 1,0; 1,6:

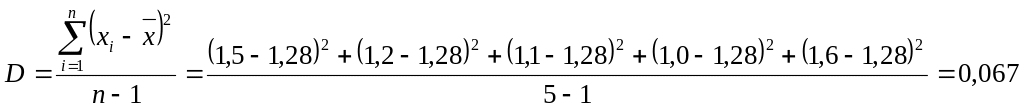
Сколько единиц стандартных отклонений надо отложить симметрично относительно среднего, чтобы охватить 40% площади под нормальной кривой?

Правило 3σ: Вероятность того, что отклонение СВ х, имеющей нормальное распределение, будет отклоняться от математического ожидания по абсолютной величине не более, чем на , равняется:

Если обозначить , то получ-ся, что ;

При Z = 1 внутрь диапазона под кривой нормального распределения попадает 68,3 % (Р = 0,6826).

Чтобы охватить 40 % площади под кривой нормального распределения, достаточно отложить симметрично относительно среднего 1 единицу стандартного отклонения Р = 0,6826 (S = 68 %).

5.5. Укажите на сходство и различие размаха, дисперсии,

среднеквадратического отклонения (СКО) значений СВ

(10 баллов). Определите связь м/у СКО СВ и СКО их

среднеарифметического значения (10 баллов).

Укажите на сходство и различие размаха, дисперсии, среднеквадратического отклонения (СКО) значений СВ

Для хар-ки рассеивания (разброса) измеренных СВ относительно среднего арифм-го знач. используют следующие хар-ки:

1. Размах R_i – разность м/у двумя экстремальными значениями x_i

На величину размаха может существенно повлиять даже одно случайное значение – промах, поэтому R используют для грубой оценки размаха.

2. Дисперсия - мера разброса данной случайной величины, т. е. её отклонения от математического ожидания.

Выборочная дисперсия равна сумме квадратов откл-ий измеренной величины x_i от среднего арифм-го значения:

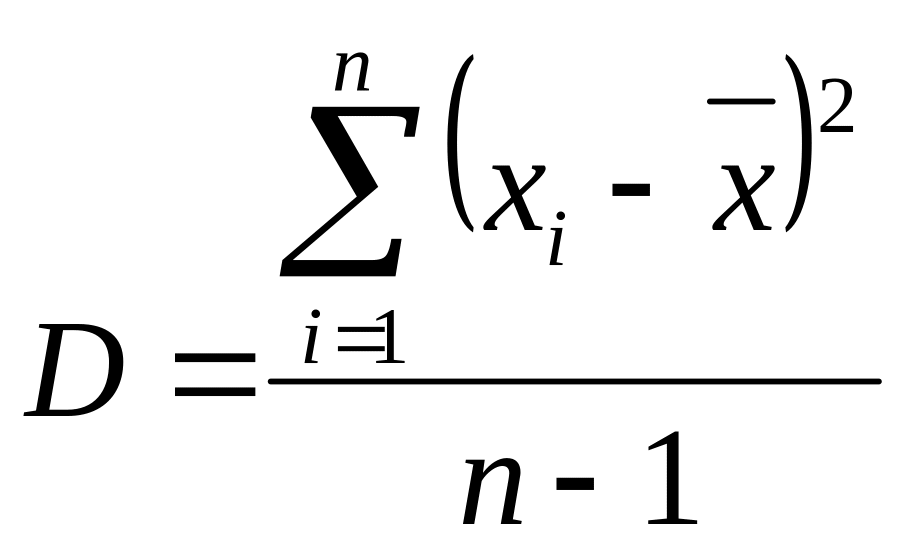
На практике чаще всего используют СКО.

3. Квадратный корень из дисперсии называется средним квадратичным отклонением

СКО - средне квадратичное (стандартное) отклонение, имеет ту же размерность, что и среднее арифметическое значение.

;