Задания для решения в аудитории
1. Решить симплексным методом задачу линейного программирования: , , , .
1.4.3. Особые случаи симплексного метода
При решении задач линейного программирования симплексным методом могут встретиться особые случаи:
1.
Если целевая функция на максимум (
),
в последней строке симплексной таблицы
нет положительных чисел, но при этом
хотя бы одно из чисел последней строки
стоящее в столбце для свободной
переменной, равно нулю, то задача имеет
бесконечное множество решений.
2.
Если целевая функция на максимум (
),
в последней строке есть хотя бы одно
положительное число, но в столбце,
соответствующем этому числу, положительных
чисел нет, то задача не имеет оптимального
решения (
)
Пример 8. Решить симплексным методом задачу линейного программирования:
,
(**),
,
.
Решение.
1.
Приведем задачу к каноническому виду.
Для этого введем балансовые переменные:
(*).
2.
Так как балансовые переменные введены
с положительным знаком (знаки балансовых
переменных совпадают со знаками свободных
членов), то они могут быть выбраны в
качестве базисных. То есть
- базисные переменные,
- свободные. Выразим базисные переменные
через свободные:
.
Отсюда
- начальное допустимое базисное решение.
Целевая функция
не
зависит от базисных переменных, то есть
уже выражена через свободные, следовательно
- значение функции в начальном решении.
3. Составим начальную симплексную таблицу используя систему (*) и целевую функцию (**).
-
1
1
1
1
0
0
7
2
1
3
0
1
0
9
3
1
4
0
0
1
12
1
1
1
0
0
0
0
min
Решение
не является оптимальным, так как в
последней строке есть положительные
числа. Все числа одинаковые, выберем
любое, например число
в столбце
(разрешающий
столбец). Для каждого положительного
числа столбца
найдем оценку
и внесем эти оценки в последний столбец
первой симплексной таблицы. Среди оценок
выберем минимальную. Таких оценок две,
выберем любую, например
.
Строка соответствующая минимальной
оценке будет разрешающей. Элемент,
стоящий на пересечении разрешающего
столбца и разрешающей строки является
разрешающим, то есть
- разрешающий.
4. Осуществим переход ко второй симплексной таблице.
Для
этого разрешающую (третью) строку
разделим на
,
чтобы разрешающий элемент был равен 1.
Затем в разрешающем столбце необходимо
получить все нули, кроме разрешающего
элемента. При этом базисная переменная
станет свободной, а
- базисной. Для этого третью строку
(после деления на
):
вычтем из первой строки (
);
умножим на
и вычтем из второй строки (
);
вычтем из четвертой строки (
).
-
1/4
3/4
0
1
0
-1/4
4
-1/4
1/4
0
0
1
-3/4
0
3/4
1/4
1
0
0
1/4
3
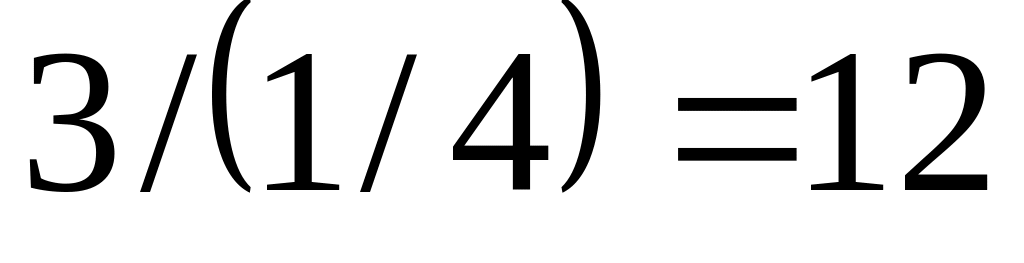
1/4
3/4
0
0
0
-1/4
-3
min
Решение
не является оптимальным, так как в
последней строке есть положительные
числа. Выберем максимальное из них
,
соответствующее столбцу
(разрешающий столбец). Для каждого
положительного числа столбца
найдем оценку
и внесем эти оценки в последний столбец
второй симплексной таблицы. Среди оценок
выберем минимальную, то есть
.
Строка соответствующая минимальной
оценке будет разрешающей. Элемент,
стоящий на пересечении разрешающего
столбца и разрешающей строки является
разрешающим, то есть
- разрешающий.
5. Осуществим переход к третьей симплексной таблице.
Для
этого разрешающую (вторую) строку
разделим на
,
чтобы разрешающий элемент был равен 1.
Затем в разрешающем столбце необходимо
получить все нули, кроме разрешающего
элемента. При этом базисная переменная
станет свободной, а
- базисной. Для этого вторую строку
(после деления на
):
умножим на
и вычтем из первой строки (
);
умножим на
и вычтем из третьей строки (
);
умножим на
и вычтем из четвертой строки (
).
-
1
0
0
1
-3
2
4
-1
1
0
0
4
-3
0
-
1
0
1
0
-1
1
3
1
0
0
0
-3
2
-3
min
Решение
не является оптимальным, так как в
последней строке есть положительные
числа. Выберем максимальное из них
,
соответствующее столбцу
(разрешающий столбец). Для каждого
положительного числа столбца
найдем оценку
и внесем эти оценки в последний столбец
второй симплексной таблицы. Среди оценок
выберем минимальную, то есть
.
Строка соответствующая минимальной
оценке будет разрешающей. Элемент,
стоящий на пересечении разрешающего
столбца и разрешающей строки является
разрешающим, то есть
- разрешающий.
6. Осуществим переход к четвертой симплексной таблице.
Для
этого разрешающую (первую) строку
разделим на
,
чтобы разрешающий элемент был равен 1.
Затем в разрешающем столбце необходимо
получить все нули, кроме разрешающего
элемента. При этом базисная переменная
станет свободной, а
- базисной. Для этого первую строку
(после деления на
):
умножим на
и вычтем из второй строки (
);
вычтем из третьей строки (
);
умножим на
и вычтем из четвертой строки (
).
-
1/2
0
0
1/2
-3/2
1
2
1/2
1
0
3/2
-1/2
0
6
1/2
0
1
-1/2
1/2
0
1
0
0
0
-1
0
0
-7
min
В
последней строке симплексной таблицы
нет положительных чисел, но при этом
есть числа стоящие в столбцах для
свободных переменных, равные нулю (при
и
).
Следовательно, максимальное значение
функции
.
Это значение может быть достигнуто на
бесконечном множестве решений. Одним
из решений этого множества является
.
Для того чтобы найти следующее решение
перейдем к пятой симплексной таблице.
7.
В последней строке нет положительных
элементов. Выберем столбец соответствующий
свободной переменной и содержащий ноль
в последней строке, например столбец
.
Среди элементов этого столбца имеется
только один положительный
.
Выберем его в качестве разрешающего.
Далее третью строку разделим на
,
чтобы разрешающий элемент был равен
.
После деления на
третью строку прибавим к первой и ко
второй. При этом базисная переменная
станет свободной, а
- базисной.
-
0
0
-1
1
-2
1
1
0
1
-1
2
-1
0
5
1
0
2
-1
1
0
2
0
0
0
-1
0
0
-7
min
Получено
новое решение
.
При этом выполненные преобразования
не повлияли на значение целевой функции:
.
Таким образом улучшить целевую функцию
нельзя, она достигла возможного максимума.
Дальнейшие преобразования симплексных таблиц можно выполнять бесконечно, при этом будут получаться различные оптимальные решения.