8. В евклидовом пространстве ортогональным преобразованием привести квадратичную форму
к каноническому виду .
(А) Записать матрицу квадратичной формы .
Для матрицы найти
(Б) характеристический многочлен;
(В) спектр , , (указать в порядке возрастания значений).
Записать
(Г) квадратичную форму (согласовать с указанным спектром);
(Д) матрицу квадратичной формы .
(Е) Найти собственные векторы , , линейного преобразования с матрицей . Можно ли из них составить ортогональную систему векторов?
(Ж) Найти ортонормированный собственный базис { , , } линейного преобразования с матрицей (в соответствии с указанной матрицей ).
(З) Записать матрицу Q ортогонального линейного преобразования квадратичной формы к каноническому виду .
(И) Чему равна матрица ?
Указание. При записи матриц, в том числе векторов, где это возможно, выносить общие множители, представляя сами матрицы в целых числах.
1. Для однородной системы уравнений:
(А) найти общее решение (в качестве базисных переменных из списка , , , выбрать с наименьшими номерами);
(Б) указать какую-либо фундаментальную систему решений.
2. Вычислить:
.
3. Представить следующую рациональную дробь в виде суммы простейших дробей:
.
4. Найти наибольший общий делитель многочленов:
f(x) = 
и g(x) = 
.
5. В линейном пространстве заданы два базиса: = { , } и = { , }:
,
,
и
,
.
(А) Найти матрицу перехода от базиса к базису .
(Б) Найти матрицу обратного перехода.
6. Следующую систему векторов евклидова пространства , заданных в ортонормированном базисе:
,
,
,
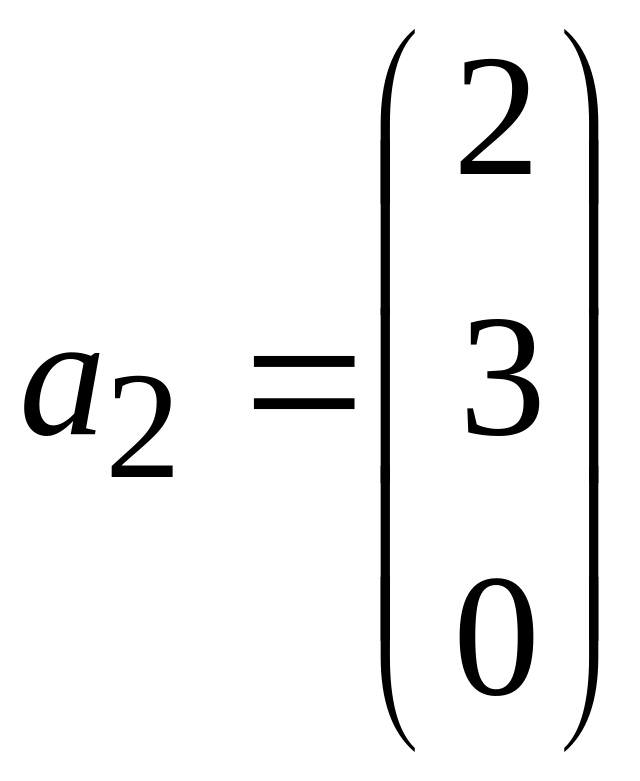(А) ортогонализировать (процесс ортогонализации начать с вектора );
(Б) полученную систему нормировать.
7. Для линейного преобразования Â линейного пространства задано разложение образов базисных векторов по базису = { , }:
,
.
Найти образ вектора в базисе , если векторы , , заданы векторами координат , , в другом, отличном от базисе = { , } этого линейного пространства :
,
;
.
(А) Чему равна матрица линейного преобразования Â в базисе ?
(Б) Найти координаты вектора в базисе .
(В) Записать разложение образа вектора по базису .
8. В евклидовом пространстве ортогональным преобразованием привести квадратичную форму
к каноническому виду .
(А) Записать матрицу квадратичной формы .
Для матрицы найти
(Б) характеристический многочлен;
(В) спектр , , (указать в порядке возрастания значений).
Записать
(Г) квадратичную форму (согласовать с указанным спектром);
(Д) матрицу квадратичной формы .
(Е) Найти собственные векторы , , линейного преобразования с матрицей . Можно ли из них составить ортогональную систему векторов?
(Ж) Найти ортонормированный собственный базис { , , } линейного преобразования с матрицей (в соответствии с указанной матрицей ).
(З) Записать матрицу Q ортогонального линейного преобразования квадратичной формы к каноническому виду .
(И) Чему равна матрица ?
Указание. При записи матриц, в том числе векторов, где это возможно, выносить общие множители, представляя сами матрицы в целых числах.
1. Для однородной системы уравнений:
(А) найти общее решение (в качестве базисных переменных из списка , , , выбрать с наименьшими номерами);
(Б) указать какую-либо фундаментальную систему решений.
2. Вычислить:
.
3. Представить следующую рациональную дробь в виде суммы простейших дробей:
.
4. Найти наибольший общий делитель многочленов:
f(x) = 
и g(x) = 
.
5. В линейном пространстве заданы два базиса: = { , } и = { , }:
,
,
и
,
.
(А) Найти матрицу перехода от базиса к базису .
(Б) Найти матрицу обратного перехода.
6. Следующую систему векторов евклидова пространства , заданных в ортонормированном базисе:
,
,
,
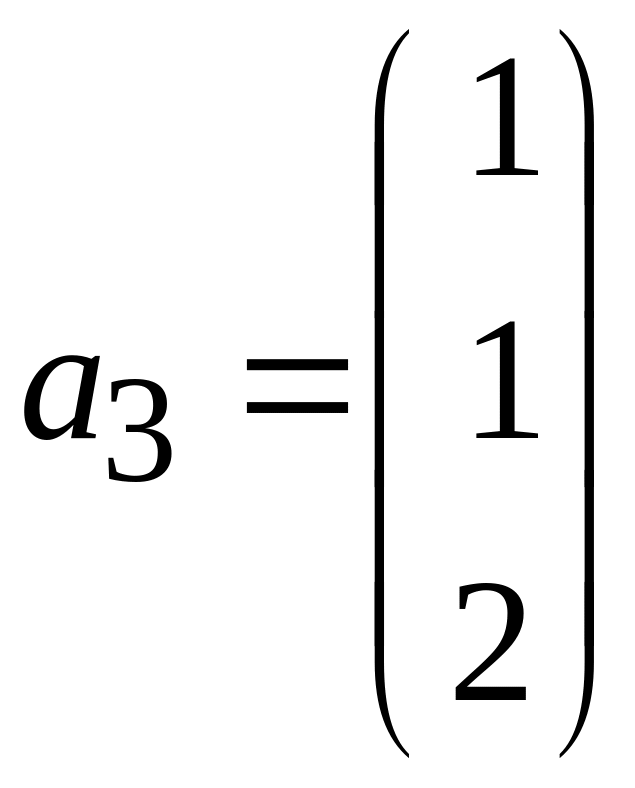(А) ортогонализировать (процесс ортогонализации начать с вектора );
(Б) полученную систему нормировать.
7. Для линейного преобразования Â линейного пространства задано разложение образов базисных векторов по базису = { , }:
,
.
Найти образ вектора в базисе , если векторы , , заданы векторами координат , , в другом, отличном от базисе = { , } этого линейного пространства :
,
;
.
(А) Чему равна матрица линейного преобразования Â в базисе ?
(Б) Найти координаты вектора в базисе .
(В) Записать разложение образа вектора по базису .