2.2. Поток вектора

Построим элементарную площадку , совмещенную с на­чалом вектора (рис. 2.2) [8, стр. 37-40].

Рисунок 2.2

Восстановим к площадке вектор ЕДИНИЧНОЙ НОРМАЛИ . Спро­ецируем на продолжение . Согласно рисунку 2.2,

, (2.4)

Поскольку - единичный вектор,

численно =

, (2.5)

где - условный вектор, модуль которого численно равен пло­щади элементарной площадки , а направление совпадает с век­тором единичной нормали.

Умножим на СКАЛЯРНО:

. (2.6)

Полученное произведение обычно обозначают и называют элементарным потоком вектора через площадку . Таким образом, из (2.4), (2.5) и (2.6) следует, что элементарный поток вектора может быть пред­ставлен в одной из трех форм записи:

. (2.7)

Согласно (2.7), поток вектора является скалярной (алгебраической) величиной. Очевидно, что >0, если и совпа­дают по направлению ( ). Если и направлены в разные стороны ( ), <0. Поток максимален по модулю при и . При , и = 0.

Заметим, что направление относительно условно и могло быть выбрано ПРОТИВОПОЛОЖНЫМ тому, которое изображено на рисунке 2.2. Однако для ЗАМКНУТЫХ поверхностей принято строить по направлению ОТ ЦЕНТРА поверхности НАРУЖУ (ортогональ­но элементарной площадке , принадлежащей поверхности). Такие нормали к поверхностям обычно называют "ПОЛОЖИТЕЛЬНЫМИ".

3. Дивергенция вектора

Зададим поле вектора , определенное в любой точке пространства x, y, z, рисунок 2.3.

Окружим точку " " в пространстве замкнутой воображаемой поверх­ностью с объемом и площадью .

Элементарный поток вектора через площадку , принад­лежащую поверхности определяется формулой (2.7). Поток вектора через всю замкнутую поверхность получим интегрированием формулы (2.7); [8, стр. 40-42]:

. (2.8)

Рисунок 2.3

Начнем уменьшать объем , равномерно "стягивая" его к точке " ". Поток станет убывать, и при , , отношение ( ) будет стремиться к некоторому пределу

, (2.9)

который называют ДИВЕРГЕНЦИЕЙ вектора в точке " ".

Физический смысл дивергенции вектора заключается в следующем:

1. Если скалярная функция >0, в точке " ", рисунок 2.3 существует источник поля вектора .

2. Если <0 , в точке " " имеет место "СТОК" вектор­ного поля.

3. При = 0 - в точке " " отсутствуют как источники, так и стоки, поля (либо число источников равно числу идентичных им "стоков").

Согласно (2.9)

. (2.10)

В трехмерной системе координат поток элементарного объема можно представить в виде суммы трех элементар­ных потоков вдоль осей , , :

. (2.11)

Элементарные вычисления слагаемых в правой части равенства (2.11), [8, стр. 40-42] дают следующие значения:

. (2.12)

Подстановка (2.12) в (2.11) позволяет представить с учетом (2.10) в следующем виде:

, (2.13)

где , , - проекции вектора на координатные оси, при условии, что начало вектора находится в точке " " (рис. 2.3). Перемножим вектор

и векторный дифференциальный оператор Гамильтона скалярно.

По правилу скалярного произведения:

,

следовательно,

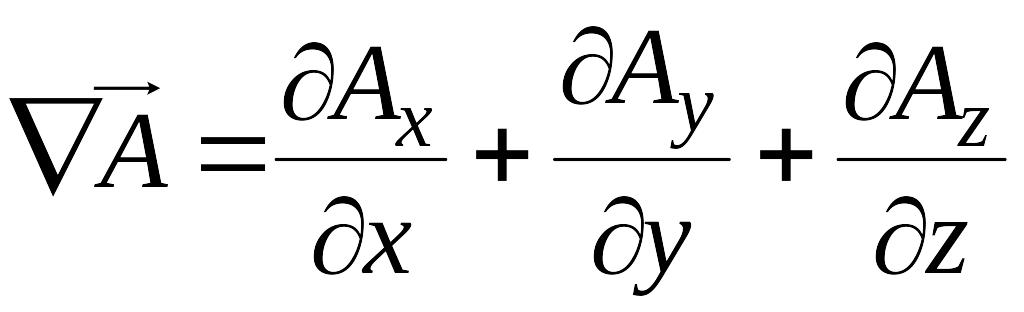. (2.14)

Из сравнения (2.13) и (2.14) видно, что дивергенция вектора может быть записана в виде:

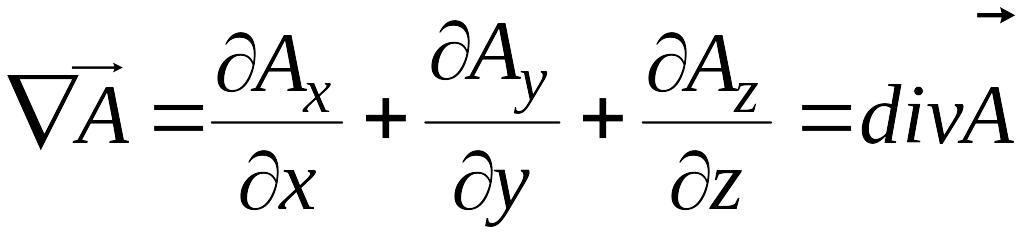. (2.15)