Глава 17. Основы фотометрии

1. Энергетические и фотометрические характеристики оптического излучения

2. Функция видности и её зависимость от длины электромагнитной волны

3. Телесный угол, световой поток и механический эквивалент света

4. Сила света

5. Освещённость поверхности

6. Закон освещённости

7. Светимость излучающей поверхности конечных размеров

8. Яркость светящейся поверхности

9. Справочные данные по основным фотометрическим понятиям

Контрольные вопросы к главе 17

Глава 1. Структура твёрдых тел, типы связей между ионами, дефекты в кристаллах

1. Понятие об идеальном монокристалле, элементарной ячейке, кристаллографических системах, классах и группах [1, 2]

Под "идеальным" монокристаллом понимают безграничную структуру, в которой составляющие ее частицы (ионы) расположены на повторяющихся расстояниях в любом, ус­ловно выбранном, направлении.

Цепочка ионов, расположенных на расстоянии а друг от друга вдоль одной прямой AD (рисунок 1.1) называется ионным рядом. Величине а, показанная на рисунке 1.1, но­сит название ПЕРИОДА кристаллической структуры.

Рисунок 1.1

Переместим ионный ряд АD (рисунок 1.1) на несколько периодов b параллельно самому себе таким образом, чтобы был равен . Полученная структура (рисунок 1.2) носит название ионной плос­кости.

Рисунок 1.2

Расположим линию AF под углом α к AD и под углом γ к АО, рисунок 1.3. Переместим ионную плоскость на несколько периодов С, таким образом, чтобы ион, находящийся ранее в точке А двигался вдоль AF, а вся ионная плоскость перемещалась бы параллельно самой себе. В результате, получим пространственную структуру, которую мы определили ранее как "идеальный" монокрис­талл.

Геометрическое место точек, в которых находятся ионы, называется УЗЛАМИ кристаллической структуры (рисунок 1.3).

Области пространства, расположенные между ионами структуры называются МЕЖДОУЗЛИЯМИ (рисунок 1.3).

Выберем в "построенной" монокристаллической структуре мини­мальный объем , который полностью отражает геометрию струк­туры и ее наполнение ионами. Очевидно, что выбранная таким образом часть структуры, в простейшем общем случае, будет иметь форму косо­го параллелепипеда со сторонами а, b, с и углами α, β, γ , в котором находится один ион (рисунок 1.4).

Рисунок 1.3

Минимальная часть монокристалла, полностью отражаю­щая его геометрические характеристики и заполнение ионами, называется ЭЛЕМЕНТАРНОЙ ЯЧЕЙКОЙ.

С этой точки зрения, выполненное выше "построение" монокристаллической структуры можно представить себе как ТРАНСЛЯЦИЮ (переме­щение) элементарной ячейки на фиксированные расстояния (а, b, с) вдоль направлений - соответственно. При этом, за каждый акт трансляции, ион, находящийся исходно в точке (А) ос­тавляет как бы "отпечаток" на линиях в виде такого же иона. В результате получается пространственная структура соот­ветствующая рисунку 1.3.

По форме элементарных ячеек (т.е. по соотношению между (а, b, с) и (α, β, γ)) все монокристаллы в природе делятся на 7 кристаллографических СИСТЕМ:

Рисунок 1.4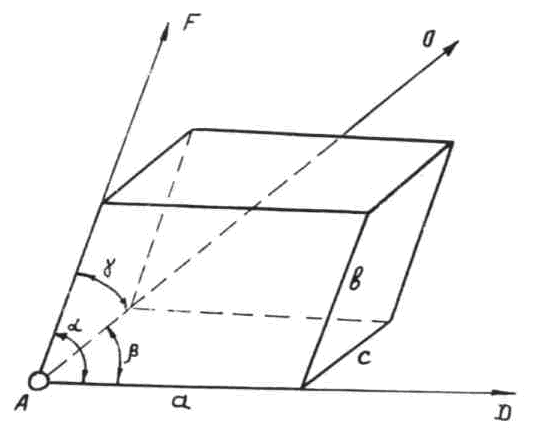

1.Триклинная: ; ,

2.Μο ноклинная: ; ,

3.Ромбоэдрическая: ; ,

4.Тетрагональная: ; ,

5.Гексагональная: ; ,

6.Ромбическая: ; ,

7.К у бическая: ; .

По плотности упаковки ионами системы делятся на классы. Например, кубическая система имеет 3 класса: простая кубическая (рис. 1.5), кубическая объемно-центрированная (рис. 1.6), кубическая гранецентрированная (рис. 1.7). Общее число классов во всех 7 сис­темах равно 32.

По типу симметрии классы делятся на группы. Все многообра­зие кристаллографических групп, существующих в природе, насчиты­вает 230 различных модификаций. Кристаллографические группы носят название ФЕДОРОВСКИХ по имени их первооткрывателя Фёдорова Евграфа Степановича (I853-I9I9) - великого русского кристаллографа.

Рисунок 1.5

Рисунок 1.6 Рисунок 1.7