Основы статистической динамики рынка ценных бумаг - Кремер А.И

инструментах. Это означает, что участники рынка не могут использовать такую информацию для систематического увеличения выгоды от совершаемых сделок. Действительно, любая информация подобного рода уже отражена в сложившихся рыночных ценах и потому в дальнейшем теряет свою ценность. Отсюда можно сделать вывод, что не имеет смысла прилагать усилия для уточнения имеющейся информации. Причина здесь в том, что дополнительная информация все равно отобразится в ценах, известных всем участникам рынка, так что усилия, приложенные одним из участников рынка, не оправдают себя.

Таким образом, гипотеза в сильной форме утверждает, что в рыночных ценах отражена вся имеющаяся у кого-либо информация. Строго говоря, это утверждение нельзя считать реалистическим, поскольку оно приводит к противоречию: если никто не добывает новой информации об объектах купли-продажи, то появляется стимул к ее получению. Однако стоит кому-либо из участников рынка приложить усилия и добыть дополнительную информацию, как она тут же становится общедоступной, не принося своему первоначальному владельцу никаких преимуществ.

Одну из возможностей разрешения этого противоречия дает модель рациональных ожиданий с помехами [ 4 ]. В этой модели считается, что цены отображают рыночную информацию не полностью, поэтому при принятии своих решений участники рынка используют как собственную информацию, так и ту, что содержится в ценах.

Гипотеза в квазисильной форме гласит, что цены отображают не полную, а лишь общедоступную информацию об объектах купли-продажи.

Наконец, гипотеза об эффективности рынка в слабой форме утверждает, что текущие цены отражают всю ту информацию, которую можно извлечь из прошлых цен. Именно эта форма гипотезы чаще всего тестируется на практике и используется при моделировании изменений цен на финансовые инструменты с течением времени.

2.2.Марковские свойства цен акций и гипотеза случайного блуждания

11

В1827 г. английский ботаник Р.Броун (R.Brown) наблюдал в микроскоп движение цветочной пыльцы, взвешенной в воде. Наблюдаемые частицы совершали неупорядоченные независимые движения, описывая сложные зигзагообразные траектории («броуновское движение» или случайное блуждание). Позднее было установлено, что причина броуновского движения заключается в хаотическом движении молекул жидкости, случайные удары которых заставляют взвешенную в жидкости частицу описывать случайные траектории. Исследования броуновского движения явились фактором, способствовавшим развитию теории случайных процессов.

Современные математические модели случайного блуждания основаны на теории марковских процессов [ 5 ]. Марковский процесс является особым типом случайного процесса, в котором для предсказания будущих значений случайной переменной используется только ее текущее значение. Вся предыдущая история переменной и путь, по которому из прошлых значений сформировалось текущее значение, не играют роли.

В1900 г. французский экономист Л.Башелье выдвинул гипотезу, что движение цен на товарных рынках Франции по своему характеру аналогично броуновскому движению. В 1950-1960-е гг. идея Л.Башелье нашла подтверждение в исследованиях закономерностей, которые определяют колебания цен на акции. Но если легкая частица, взвешенная в жидкости, совершает случайное блуждание в трехмерном пространстве, то цена акции испытывает одномерные блуждания.

При этом наилучшее подтверждение получила модель, в соответствии с которой случайные приращения цены распределены по нормальному закону. Гипотеза о случайном блуждании цен на акции аналогична гипотезе об эффективности рынка в слабой форме. Действительно, обе гипотезы утверждают, что последующая цена финансового инструмента связана лишь с ее текущим значением.

На эффективном фондовом рынке цены финансовых инструментов находятся в равновесии. Эти цены будут изменяться только при получении участниками рынка новой информации. Такая информация может вызывать как положительные, так и отрицательные ожидания изменения рыночной ситуации. В ре-

12

зультате очередное изменение цены может иметь как положительное, так и отрицательное значение.

Рис. 3. Движение средних цен акций АО "Челябинский трубопрокатный завод" в 1995-1996 гг. Нижняя линия - цена покупки, верхняя - цена продажи, средняя - курсовая цена (средняя арифметическая цен покупки и продажи).

На рис.3 представлена динамика средних цен акций АО "Челябинский трубопрокатный завод" с января 1995 г. по февраль 1996 г. [ 9 ]. Ход кривых на рисунке позволяет предположить, что математическую модель движения цен составят случайные блуждания в сумме с линейным трендом.

Рис.4. Динамика средних цен акций АО "Синарский трубный завод" в 1995-

1996 гг.

На рис.4 представлена динамика средних цен АО "Синарский трубный завод" за период с января 1995 г. по февраль 1996 г. [ 9 ]. Несмотря на заметные отличия характера движения от примера на рис.3, модель случайного блуждания цен вполне применима и здесь.

13

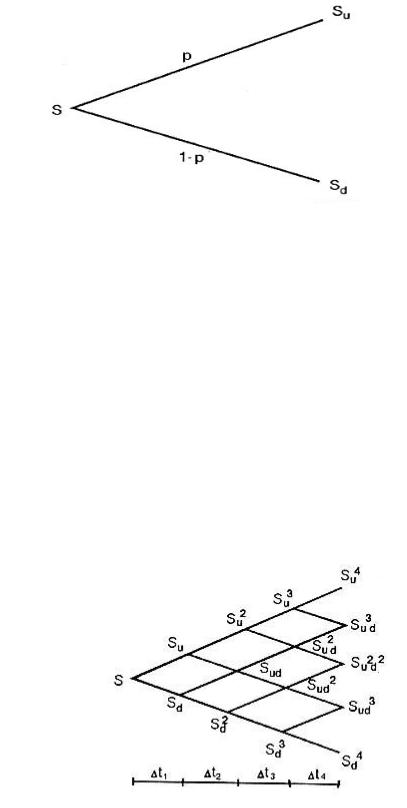
Рис. 6. Дерево распределения курсовой цены акции для четырех временных интервалов.

Построение дерева на отрезке времени длиной 4∆ t показано на рис.6. Здесь начальная цена акции равна S . Итак, по завершении первого интервала ∆ t1

цена ее может составить S u или S d . По завершении второго интервала ∆ t2

цена может принять одно из трех значений: S u2, S d 2 или S u d . По заверше-

нии третьего интервала ∆ t3 - одно из четырех значений: S u3 , S d 3 , S u2 d

или S u d 2, и т.д. В целях упрощения модели, поскольку период наблюдения за ценой обычно дробится на большое число интервалов, часто делается допущение,

что u = d1 . С учетом того, что при этом ud = 1, значения цен акции на дереве рас-

пределения можно представить следующим образом (рис.7).

Рис. 7. Дерево распределения цены акции при ud = 1.

Таким образом, биномиальная модель порождает бинарное дерево, в каждой точке ветвления (узле) которого есть возможность как подъема, так и падения цены акции.

Для упрощения расчетов наращенных и дисконтируемых сумм будем использовать безрисковую процентную ставку r в модели непрерывно начисляемых сложных процентов ( см. Приложение 1). Пусть в начале наблюдения цена акции равна S .Тогда, согласно представлениям финансовой математики, ожидаемое значение цены акции спустя время ∆ t должно составить S er∆ t , где er∆ t - мно-

15

житель наращения ( см. Приложение 1). С другой стороны, за время ∆ t цена акции сформируется случайным образом, причем с вероятностью p она примет

значение Su , а с вероятностью 1− p - значение Sd . Поэтому математическое

Формула (1) позволяет рассчитать вероятность повышения и понижения цены акции.

Пример расчетов. Цена акции в начале периода равна 40 руб., среднеквадратическое отклонение составляет 35%, безрисковая процентная ставка равна 10% годовых. Найти вероятность повышения и понижения цены акции через 1 месяц, а также возможные значения курса акций последовательно через 1 и 2 месяца.

Решение. Одному месяцу соответствует 0,0833 календарного года, откуда

16

Sd 2 = 40 0,8170 = 32,68 (руб.). Решение закончено.

Для бинарного дерева характерно то, что переход в любую промежуточную точку ветвления не зависит от траектории, по которой мы в нее попали. Важно лишь общее количество подъемов и спадов, которое претерпевает цена акции на пути в эту точку.

Если мы не используем дополнительных вероятностных моделей риска участников рынка, то бинарное дерево отображает последовательность независимых испытаний (схему Бернулли): на каждом интервале длительностью ∆ t как будто происходит случайный опыт, в результате которого цена акции может либо возрасти, либо уменьшиться. При этом «траектории» движения цен характеризуются случайными блужданиями по решетке, образованной ветвями бинарного дерева. Решетка, по которой происходят эти блуждания, может быть сколь угодно обширной, поскольку необязательно выбирать интервалы длиной в один месяц или год. На самом деле структура биномиальной модели зависит только от нашего выбора, и мы может задать шаги любой длины ∆ t – суточные, часовые, минутные и т.п. Чем короче выбранный шаг, тем точнее биномиальная модель.

Рассмотрим теперь биномиальную модель на периоде длиной n ∆ t ( n ин-

тервалов наблюдения), не предполагая, что обязательно u = 1d . По завершении

этого периода общее выражение для цены акции можно записать как Su jd n− j . Такая курсовая цена акции сложится, если на пути в соответствующую точку де-

подобной траектории будет равна, в силу независимости случайных подъемов и спадов, p j (1− p)n− j . При этом порядок подъемов и спадов не имеет значения.

Количество траекторий блуждания по решетке, приводящих в выбранную точку дерева, определяется обычным биномиальным коэффициентом -

17

Следовательно, каждой точке ветвления бинарного дерева соответствует свой биномиальный коэффициент, т.е. расположение точек ветвления (начиная со второго интервала времени наблюдения) совпадает с расположением чисел в треугольнике Паскаля (рис.8).

1 1

1 2 1

13 3 1

1 4 6 4 1

1 5 10 10 5 1

1 6 15 20 15 6 1

………………………….

………………………………

Рис. 8. Треугольник Паскаля. Расположение чисел (биномиальных коэффициентов) совпадает с расположением соответствующих узлов бинарного дерева.

Таким образом, по завершении периода наблюдения длительностью n∆ t

наблюдения. Следовательно, в рамках биномиальной модели вероятность формирования той или иной случайной цены акции подчиняется биномиальному закону распределения.

В соответствии со свойствами биномиального закона распределения вероятностей легко найти наивероятнейшее число j0 подъемов цены акции за время

лучаем наивероятнейшее значение цены акции - Su j0 d n− j0 , которое реализуется с вероятностью Pj0,n, наибольшей из всех вероятностей P j,n .

2.4.Экспоненциальная биномиальная модель

Многие исследователи фондового рынка полагают, что случайное блуждание демонстрируют не сами цены, а натуральные логарифмы их значений [ 8, 9 ]. Тогда цена акции к концу n-го интервала наблюдения Sn может быть

18

Изменение цены акции в будущем – это случайный процесс. Если ввести в

модель движения цены непрерывный отсчет времени t , то для любого момента времени tk и любого τ > 0 , случайная величина

окажется распределенной по гауссовому закону. Из этого результата следует важный вывод: в рамках экспоненциальной биномиальной модели отношение цен акции, наблюденных через любой промежуток времени, подчиняется логарифмиче-

ски-нормальному распределению.

Изначально можно было предположить, что в целях вероятностной оценки стоимости акции следует воспользоваться гауссовым распределением. Почему же в теории и практике прогнозирования цен акций принято использовать логариф- мически-нормальное распределение [ 3, 8 ]? Это обусловлено следующими причинами. Во-первых, гауссово распределение имеет симметричную кривую относительно своей центральной оси и может давать как положительные, так и отрицательные значения. Во-вторых, гауссово распределение говорит о равной вероятности цены актива пойти как вверх, так и вниз. В то же время в практике рынка ценных бумаг всегда присутствует инфляция, которая оказывает давление на цены в сторону их повышения. В связи с этим в моделях вероятностного прогнозирования цен следует использовать логарифмически-нормальное распределение. Кривая этого распределения всегда соответствует только положительным значениям случайной величины и имеет правостороннюю скошенность, т.е. характеризуется положительным значением коэффициента асимметрии. Следовательно, согласно данному распределению, цена акции имеет большую вероятность пойти вверх, чем вниз.

19

Отметим, что отношение S(tk + τ ) S(tk ) характеризует среднюю доход-

ность финансового инструмента на отрезке времени [tk , tk + τ ]. В сущности, это

отношение равно множителю наращения в экспоненциальной форме, используемого в модели непрерывного начисления сложных процентов (см. Приложение 1).

2.5. Об использовании в моделях ценообразования акций непрерывнозначных марковских процессов

Модели поведения цен на акции в непрерывном времени обычно строятся на основе винеровского процесса [ 5 ], который является частным случаем марковского случайного процесса. В физике именно винеровский процесс используется для описания броуновского движения легкой частицы, испытывающей большое число слабых ударов от молекул жидкости.

На любом интервале времени длиной T приращение случайной величины z , которая следует винеровскому процессу, подчиняется гауссовскому распределению с нулевым математическим ожиданием и стандартным отклонением, равным T .При этом для построения математических моделей используется аппарат стохастических дифференциальных уравнений.

Рис. 9. Пример реализации винеровского процесса и обобщенного винеровского процесса.

Обобщенный винеровский процесс для переменной x (цены акции) подчиняется стохастическому дифференциальному уравнению [ 8 ]

20