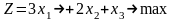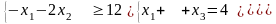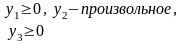- •1 Линейное программирование
- •1.1 Математические модели задач планирования и управления. Общая постановка задачи оптимизации
- •1.2 Формы записи задач линейного программирования и их эквивалентность. Приведение задачи к каноническому виду.
- •Геометрическая интерпретация и графическое решение задач линейного программирования
- •Нахождение начального опорного плана задач линейного программирования
- •Симплекс-метод решения задач линейного программирования
- •Линейное программирование
- •Метод искусственного базиса
- •Двойственность в линейном программировании
- •Двойственность в линейном программировании
- •Двойственный симплекс-метод
- •Специальные задачи линейного программирования Математические модели задач транспортного типа
- •Методы решения транспортной задачи Построение начального опорного плана методом «минимального элемента»
- •Решение транспортной задачи методом потенциалов
Двойственность в линейном программировании
Пусть имеется симметричная пара взаимно двойственных задач
Прямая задача , , . |
Двойственная задача
, . |
Основное
неравенство теории двойственности.
Для любых допустимых планов
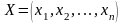 и
и
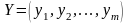 прямой и двойственной задач всегда
справедливо неравенство
прямой и двойственной задач всегда
справедливо неравенство
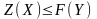 или
или
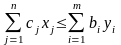 .
.
Экономическое содержание неравенства означает, что для любых допустимых плановX и Y общая стоимость не превосходит суммарной оценка ресурсов.
Достаточный
признак оптимальности.
Если для некоторых допустимых планов
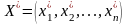 и
и
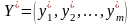 пары
двойственных задач выполняется
неравенство
пары
двойственных задач выполняется
неравенство
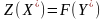 ,
то
и
,
то
и
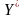 оптимальными планами соответствующих
задач.
оптимальными планами соответствующих
задач.
Экономический смысл теоремы состоит в том, что план и вектор оценки ресурсов являются оптимальными, если цена всей произведенной продукции и суммарная оценка ресурсов совпадают.
Принцип двойственности. Если одна из двойственных задач имеет оптимальное решение, то и другая также имеет оптимальное решение, притом для оптимальных планов и выполняется равенство . Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых планов, то система ограничений другой задачи противоречива.
Следствие (теорема существования оптимальных планов). Для существования оптимального плана любой из пары двойственных задач необходимо и достаточно существование допустимого плана для каждой.
Экономическая интерпретация принципа двойственности состоит в том, что план производства и вектор оценок ресурсов являются оптимальными тогда и только тогда, когда цена произведенной продукции равна суммарной оценке ресурсов, т.е. оценки выступают как инструмент балансирования затрат и результатов. Двойственные оценки обладают тем свойством, что гарантируют рентабельность оптимального плана (т.е. равенство оценки продуктов и ресурсов) и обуславливают убыточность всякого другого плана, отличного от оптимального. Двойственные оценки позволяют сопоставить и сбалансировать затраты и результаты решения.
Теорема о дополняющей нежесткости. Для оптимальности допустимых планов и прямой и двойственной задач необходимо и достаточно, чтобы выполнялись соотношения
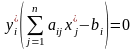 ,
(1.53)
,
(1.53)
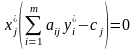 ,
. (1.54)
,
. (1.54)
Условия (1.53), (1.54) называются условиями дополняющей нежесткости. Из них следует: если какое-либо ограничение одной из задач ее оптимальным планом обращается в строгое неравенство, то соответствующая компонента оптимального плана двойственной задачи должна равняться нулю; если же какая-либо компонента оптимального плана одной из задач положительна, то соответствующее ограничение в двойственной задаче ее оптимальным планом должно обращаться в строгое равенство.
Пример 7.Дана пара взаимно двойственных задач
Прямая задача
. |
Двойственная задача
|
Зная оптимальное решение прямой задачи, выписать ответ двойственной задачи. Дать экономическую интерпретацию двойственных оценок.
Решение.
Базисным
переменным прямой задачи
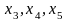 поставим в соответствие свободные
переменные двойственной задачи
поставим в соответствие свободные
переменные двойственной задачи
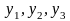 в 1-й и последней симплекс-таблице примера
4:
в 1-й и последней симплекс-таблице примера
4:
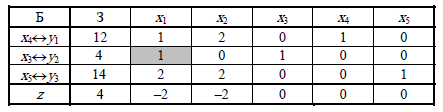
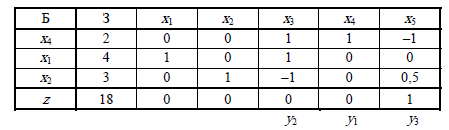
Решение двойственной задачи найдем по последней z-строке и прибавим к ним соответствующие коэффициенты целевой функции прямой задачи:
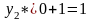 (так как в целевой
функции прямой задачи коэффициент при
равен 1);
(так как в целевой
функции прямой задачи коэффициент при
равен 1);
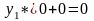 (потому что в целевую
функцию прямой задачи
(потому что в целевую
функцию прямой задачи
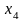 не
входит);
не
входит);
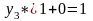 (потому что в целевую
функцию прямой задачи
(потому что в целевую
функцию прямой задачи
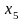 не
входит).
не
входит).
Следовательно,
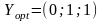 .
.
Оптимальные
двойственные оценки удовлетворяют всем
условиям двойственной задачи. При этом
минимальное значение целевой функции
двойственной задачи, равное
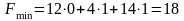 ,
совпадает с максимальным значением
целевой функции
,
совпадает с максимальным значением
целевой функции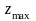 исходной задачи.
исходной задачи.
Дадим
экономическую интерпретацию двойственных
оценок. Переменные
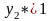 и
и
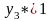 обозначают оценки единицы заготовок
соответственно 2-го и 3-го видов
соответственно.Эти оценки отличны от
нуля, что означает, что заготовки 2-го и
3-го видов полностью используются при
оптимальном плане производства обуви.
обозначают оценки единицы заготовок
соответственно 2-го и 3-го видов
соответственно.Эти оценки отличны от
нуля, что означает, что заготовки 2-го и
3-го видов полностью используются при
оптимальном плане производства обуви.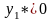 и
это означает, что заготовки 1-го вида
используются не полностью при оптимальном
плане производства обуви. Таким образом,
двойственные оценки определяют
дефицитность используемых фабрикой
заготовок, т.е. заготовки 2-го и 3-го вида
являются дефицитными, а заготовки 1-го
вида – недефицитными.
и
это означает, что заготовки 1-го вида
используются не полностью при оптимальном
плане производства обуви. Таким образом,
двойственные оценки определяют
дефицитность используемых фабрикой
заготовок, т.е. заготовки 2-го и 3-го вида
являются дефицитными, а заготовки 1-го
вида – недефицитными.
Величина оценки из двойственного плана показывает, на сколько возрастет максимальное значение целевой функции прямой задачи при увеличении количества заготовок соответствующего вида на 1 штуку.
Увеличение количества заготовок 2-го вида на 1 штуку приведет к тому, что появится возможность найти оптимальный план производства обуви, при котором общая стоимость изготовляемой обуви возрастет на ден.ед. и станет 18+1=19 ден.ед.
Аналогично,увеличение количества заготовок 3-го вида на 1 штуку приведет к тому, что появится возможность найти оптимальный план производства обуви, при котором общая стоимость изготовляемой обуви возрастет на ден.ед. и станет 18+1=19 ден.ед.

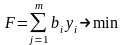 ,
,