
Методы и средства оперативного анализа случайных процессов - Пивоваров Ю.Н., Тарасов В.Н., Селищев Д.Н
.pdfτ
τ
k1
k 3
= |
∞∫e−ατ dτ = |
|
1 |
; τk 2 |
= ∞∫e−ατ dτ = |
|
1 |
; |
|||
α |
α |
||||||||||
|
0 |
|
|
0 |
|
||||||
|
|
|
|
|
|
|
|
|
|||
= ∞∫e−2ατ dτ = |
|
|
1 |
. |
|
|
|
|
|||
|
|
|
|
|
|
|
|||||
|
0 |
|
|
2α |
|
|
|
|
|||
Приближенное описание АКФ
Во-первых, АКФ может быть приближенно описана интервалом корреляции. Кроме того, для приближенного описания АКФ используются моментные характеристики этой функции.
Нормированным моментом порядка К АКФ называется величина
µk = ∞∫τ k ρx (τ)dτ . |
(1.94) |
0 |
|
Если К=0, то µk =τk , то есть интервал корреляции представляет собой
момент АКФ нулевого порядка. Для приближенного описания АКФ используется ее модель
ρM (β1 , β2 ,..., βN ,τ) ,
где β1 , β2 ,..., βN - коэффициенты (параметры) модели.
Для описания АКФ необходимо отыскать значения этих параметров, что можно проделать, используя метод моментов, согласно которому моменты истинной АКФ должны равняться моментам модели функции корреляции:
µk = µk(M ) , k =1,2,3... |
(1.95) |
Использование метода моментов позволяет достаточно точно описывать АКФ при больших значениях τ.
При малых τ более целесообразно пользоваться критериям производных, который сводится к тому, что коэффициенты модели
вычисляются |
приравниванием |
соответствующих |
производных |
нормированной АКФ и ее модели в нуле: |
|
|
|
ρx(k ) (0) = ρx (0), k =1,2,3... |
|
(1.96) |
|
51
Описание системы стационарных и стационарно связанных сигналов
Пусть имеем два случайных сигнала, которые стационарно связаны между собой.
Взаимная корреляционная функция (ВКФ) системы имеет вид:
Rxy (t1 |
|
0 |
0 |
|
,t2 ) = M X (t1 )Y (t2 ) . |
||||
|
|
|
|
|
Для описания системы двух случайных процессов необходимо знать двумерную плотность вероятности
f [X (t1 ),Y (t2 )]= f (X ,t1 + u,t2 + u). |
(1.97) |
Выражение (1.97) представляет собой условие стационарной связности. Как в случае АКФ, положим τ = t2 −t1 . Рассмотрим свойства ВКФ
системы двух стационарно связанных сигналов. 1. Так как
|
Rxy (t1 ,t2 ) = Ryx (t2 ,t1 ), |
|
|
то |
(1.98) |
|
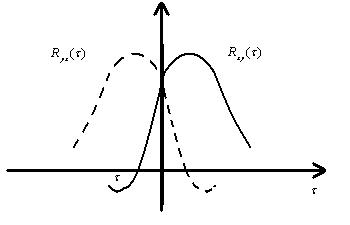
Rxy (τ) = Ryx (−τ) |
|
|
(в соответствии с рисунком 22). |
|
2. Аналогично |
|
|
|
Rxy (τ) ≤ σ xσ y ; |
(1.99) |
3. |
Rxy (0) ≠ σxσ y . |
(1.100) |
Рисунок 22График ВКФ системы двух стационарно связанных сигналов
Нормированная функция взаимной корреляции:
52
ρxy (τ) = |
Rxy (τ) |
(1.101) |
||||
σ |
x |
σ |
y |
|||
|
|
|||||
|
|
|
|
|||
обладает аналогичными свойствами:
1)ρxy (τ) = ρxy (−τ);
2)ρxy (τ) ≤1.
Для приближенного описания ВКФ используется ряд характеристик: координата и величина экстремума, интервал взаимной корреляции, моментные характеристики и производные ВКФ при различных значениях аргументах.
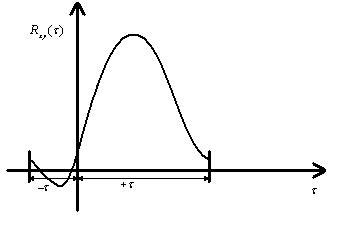
Интервал взаимной корреляции двух стационарно связанных случайных сигналов определяется как интервал времени, внутри которого ВКФ отлична от нуля, а вне его – равна или близка к нулю (в соответствии с рисунком 23).
Рисунок 23 – К вопросу об определении интервала взаимной корреляции
Способы отыскания сходны со способами определения интервала корреляции с отличием, что в данном случае приходится оценивать взаимодействие как в положительной, так и в отрицательной области.
1) ρxy (τ) = δ ; |
|
(1.102) |
|||||||||
2) τкв = ∞∫ρxy (τ)dτ = ∫0 ρxy (τ)dτ + ∞∫ρxy (τ)dτ = |
|||||||||||
|
−∞ |
−∞ |
0 |
||||||||
|
= ∞∫ρxy (τ)dτ + |
∞∫ρxy (τ)dτ; |
(1.103) |
||||||||
|
0 |
|
|
|
|
|
|
|
|
0 |
|
3) τкв |
= ∞∫ |
|
|
ρxy (τ) |
|
|
dτ; |
|
(1.104) |
||
|
|
|
|
|
|||||||
|
−∞ |
|
|
||||||||
4) τкв |
= ∞∫ |
|
ρxy2 (τ) |
|
dτ . |
|
(1.105) |
||||
|
|
|
|||||||||
|
−∞ |
|
|
||||||||
53
Так же, как и в случае АКФ, для приближенного описания ВКФ используют ее моменты, которые определяются следующим образом:
∞
µxy(q) = ∫τ q ρxy (τ)dτ, (1.106)
−∞
где q- порядок момента.
Если известна координата максимального значения ВКФ, то можно использовать и такие моменты:
εxy(q) = ∞∫(τ −τ0 )q ρxy (τ)dτ . |
(1.107) |
−∞ |
|
1.2.6 Обобщенные модели случайных процессов (по Пугачеву)
Всякий случайный процесс может быть представлен в виде:
0 |
(1.108) |
X (t) = mx (t) + X (t) |
|
и описан моделью: |
|
∞ |
|
X (t) = mx (t) + ∑U kϕk (t), |
(1.109) |
k =1
где Uk - коэффициенты разложения случайной величины; ϕk - координатные, детерминированные функции.
В качестве критерия адекватности модели исследуемому сигналу можно взять критерий минимума среднеквадратической погрешности:
∆ = M [{X M (t) − X (t)}2 ]= min, |
(1.110) |
∞ |
|
M [X M (t)]= M [mx (t)]+ ∑M [U k ]ϕk (t). |
(1.111) |
k =1
Чтобы обеспечить равенство математических ожиданий модели и сигнала необходимо, чтобы сумма равнялась нулю. Это возможно, когда все случайные величины Uk центрированы. Дальнейшее построение модели сводится к отысканию Uk.
∆ = min
54
0 |
|
∞ |
|
|
|
|
(1.112) |
X M (t) = |
∑U kϕk (t) |
|
|
||||
|
|
k =1 |
|
|
|
|
|
|
0 |
0 |
2 |
|
= min . |
(1.113) |
|
∆ = M X M (t) − X (t) |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это выполняется при |
|
∂∆ |
|
= 0, |
|
||
|
∂ϕk (t) |
|
|||||
|
|
|
|
|
|
||
или
Но
∂∆ |
|
|
0 |
|
0 |
|
|
0 |
|
|
|
||||
|
|
|
∂ X M |
|
|
||||||||||
|
|
|
|
= M X M (t) |
− X (t) |
|
|
|
= 0. |
||||||
∂ϕ |
|
(t) |
∂ϕ |
|
|
||||||||||
k |
|
|
|
|
|
|
k |
(t) |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ X M |
=U k , |
|
|
|
|
|
|
|
|
|
||||
|
∂ϕk (t) |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
M |
|
0 |
|
|
0 |
|
|
= 0, |
|
|
|
|
|
||
X M (t) − |
X (t) U k |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отсюда
0 |
(t)U k |
|
0 |
, |
(1.114) |
M X M |
= M X (t)U k |
||||
|
|
|
|
|
|
∞ |
|
|
0 |
|
(1.115) |
∑M [U mU k ]ϕm (t) = |
M X (t)U k , k = 0,1,...∞. |
||||
m=1 |
|
|
|
|
|
Это нереально, поэтому кроме требования центрированности, накладываем еще одно условие
M [U m (t)U k (t)]= Rm,k .
Для того чтобы избежать необходимости решать систему уравнений, потребуем выполнения условия ортогональности
D |
, m = k |
(1.116) |
|
Rm,k = |
k |
m ≠ k |
|
|
0, |
|
|
то есть случайные величины U должны быть некоррелированными.
0 2 |
|
= Dk , |
|
|
|
|
|
M U k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
, |
k =1,2,3,... |
(1.117) |
Dkϕk (t) = M U k X (t) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
55 |
Вместо системы уравнений получаем совокупность уравнений, каждое из которых имеет единственное неизвестное.
Определяем координатные функции
|
|
0 |
|
|
|
M U k X (t) |
|
||
ϕk (t) = |
|
|
|
(1.118) |
|
Dk |
|
||
|
|
|
|
|
при известной дисперсии.
Или наоборот, задаваясь координатными функциями, отыскиваем дисперсии:
|
|
0 |
|
|
|
|
M U k X |
(t) |
|
||
Dk = |
|
|
|
. |
(1.119) |
|
ϕk (t) |
|
|||
|
|
|
|
|
|
Вывод: любой случайный процесс X(t) можно описать моделью
∞
X M (t) = mx (t) + ∑U kϕk (t),
k =1
причем математические ожидания модели и сигналы должны совпадать, а коэффициенты разложения представляют центрированные и некоррелированные случайные величины.
|
0 |
|
. |
Dkϕk (t) = M U k X (t) |
|
||
|
|
|
|
|
|
|
|
Так как |
Dkϕk (t) ≠ 0 , то и |
|
0 |
|
≠ 0 |
, следовательно, любой |
M U k X (t) |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
коэффициент разложения должен быть коррелирован с самим сигналом X(t). Вычислим минимальное значение среднеквадратической погрешности.
Итак, центрированная модель имеет вид
0 N
X M (t) = ∑U kϕk (t)
k =1
Среднеквадратическая погрешность определяется выражением
|
0 |
0 |
|
2 |
|
∆ = M X M (t) − X (t) |
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
Или
56
0 2
∆= M X M (t) −
0
2M X M (t)
0 |
|
|
0 2 |
|
X (t) |
+ M X |
(t) |
||
|
|
|
|
|
причем последнее слагаемое равно дисперсии исследуемого сигнала.
0 |
|
N |
N |
|
|
|
|
|
N |
X M2 (t) = ∑∑ϕk (t)ϕm (t)M [U kU m ]= ∑Dkϕk2 (t), |
|||||||||
|
|
k =1 m=1 |
|
|
|
|
|
k =1 |
|
0 |
|
0 |
|
∞ |
|
|
0 |
|
|
X M (t) X (t) |
= ∑U kϕk (t) X (t), |
|
|
||||||
|
|
|
k =1 |
|
|
|
|
|
|
M |
0 |
0 |
|
|
∞ |
|
0 |
|
|
X M (t) X (t) |
= ∑ϕk (t)M U k X (t) , |
||||||||
|
|
|
|
|
|
k =1 |
|
|
|
но |
|
|
|
N |
|
|
|
|
|
M |
|
0 |
|
2 |
(t) , то есть |
|
|||
U k X (t) = |
∑Dkϕk |
|
|||||||
|
|
|
|
k =1 |
|
|
|
|
|
M |
0 |
0 |
|
|
N |
2 |
|
|
|
X M (t) X (t) |
= ∑Dkϕk (t) , |
|
|
||||||
|
|
|
|
|
|
k =1 |
|
|
|
NN
∆min = Dx (t) − 2∑Dkϕk2 (t) + ∑Dkϕk2 (t) ,
k =1 |
k =1 |
N |
|
∆min = Dx (t) − ∑Dkϕk2 (t) . |
(1.120) |
k =1 |
|
Отсюда видно, что среднеквадратическая погрешность убывает до нуля, когда N стремится к бесконечности.
N
Выражение ∑Dkϕk2 (t) , будем считать дисперсией модели.
k =1
Минимальную среднеквадратическую погрешность чисто формально можно представить в виде
|
N |
|
|
|
|
∆min = Rx (t,t1 ) − ∑Dkϕk (t)ϕk (t1 ) |
|
t = t1` . |
(1.121) |
||
|
|||||
|
k =1 |
|
|
|
|
где Rx(t,t1) - АКФ сигнала. Отсюда можно предложить, что
N
∑Dkϕk (t)ϕk (t1 ) = RM (t,t1 ) − АКФ модели.
k =1
Обратимся к модели и найдем ее функцию корреляции:
|
0 |
0 |
|
= |
RM (t,t1 ) = M X M (t) X (t) |
||||
|
|
|
|
|
57
N N |
|
N N |
= M ∑∑ϕk (t)ϕm (t1 )U kU m |
= ∑∑ϕk (t)ϕm (t1 )M [U kU m ]= |
|
k =1 m=1 |
|
k =1 m=1 |
N |
|
|
= ∑Dkϕk (t)ϕk (t1 ) , |
|
(1.122) |
k =1
то есть, наше предложение о виде АКФ модели верно.
Таким образом, минимум среднеквадратической погрешности определяется выражением
∆min = {Rx (t,t1 ) − RM (t,t1 )} |
|
t = t1 . |
(1.123) |
|
Выводы.
1. В качестве модели АКФ случайного процесса можно брать ее каноническую модель:
N
RM (t,t1 )∑Dkϕk (t)ϕk (t1 ),
k=1
ичем точнее модель АКФ, тем точнее будет модель самого сигнала.
2. Из выражения для канонической модели АКФ вытекает каноническая модель сигнала, и для построения последней необходимо предварительно синтезировать каноническую модель его функции корреляции.
1.2.7Математическое описание стационарных случайных сигналов в частотной области
Настоящий раздел посвящен рассмотрению частотных, или спектральных свойств стационарных случайных процессов. В зависимости от того, на ограниченном или неограниченном промежутке времени исследуется сигнал, эти свойства разительно отличаются друг от друга.
Спектральное представление стационарного сигнала, рассматриваемого на ограниченном интервале времени
0
Пусть X (t) - центрированный стационарный случайный процесс на участке 0 ≤ t ≤ T , а Rx (t,t1 ) - АКФ этого процесса.
0
Так как X (t) - стационарный сигнал, то его корреляционная функция является функцией одного аргумента:
Rx (t,t1 ) = Rx (t1 −t) = Rx (τ),
где τ = t1 −t . Найдем диапазон изменения:
58

0 ≤ t ≤ T |
−T ≤ t1 |
−t ≤ T; |
−T ≤τ ≤ T . |
|
|||
0 ≤ t1 ≤ T |
|
|
|
На рисунке 24 изображен график зависимости АКФ от интервала между сечениями.
Рисунок 24 – График АКФ, ограниченного во времени стационарного случайного процесса
Построим каноническую модель АКФ, для этого представим ее в виде тригонометрического ряда Фурье:
|
|
|
|
|
|
|
b0 |
|
∞ |
∞ |
|
|||
|
|
Rx (τ) = |
|
+ ∑bk cos(kwτ) + ∑λk sin(kwτ). |
(1.124) |
|||||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
2 |
|
|
k =1 |
k =1 |
|
||||
Определим коэффициенты ряда: |
|
|||||||||||||
|
|
|
|
|
|
|
T0 |
|
|
|
|
|
|
|
|
|
bk = |
2 |
|
|
∫2 |
Rx (τ) cos(kwτ)dτ ; |
|
|
|||||
|
|
T |
|
|
|
|
||||||||
|
|
|
|
−T |
|
|
|
|
|
|||||
|
|
|
0 |
|
0 |
|
|
|
|
|
||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
T0 |
|
|
|
|
|
|
|
|
λk = |
2 |
|
|
|
∫2 |
|
Rx (τ)sin(kwτ)dτ , |
|
|
|||
|
|
|
T |
|
|
|
|
|
||||||
|
|
|
|
|
−T |
|
|
|
|
|
||||
|
|
|
0 |
0 |
|
|
|
|
||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
w = |
2π |
; λk = 0 , |
|
так как АКФ – четная функция своего аргумента, sin- |
||||||||||
T |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
нечетная, а интеграл от нечетной функции в симметричных пределах равен нулю;
bk = Dk , тогда
Rx (τ) = D0 + ∑∞ Dk cos(kwτ); 2 k =1
59

|
|
|
|
|
|
|
T0 |
|
|
|
Dx = |
2 |
|
|
∫2 |
|
Rx (τ) cos(kwτ)dτ , избавляемся от To: |
||||
T |
|
|||||||||
|
|
|
|
−T |
|
|
|
|||
|
|
|
0 |
0 |
|
|||||
|
|
2π |
|
2 |
2π |
= π , тогда |
||||
w = |
|
= |
||||||||
|
T |
2T |
||||||||
|
|
|
|
|
T |
|||||
|
|
|
0 |
|
|
|
|
|
|
|
Dk |
= |
1 |
T∫Rx (τ) cos(kwτ)dτ . |
|||||||
|
||||||||||
|
|
|
T −T |
|
|
|
||||
Докажем, что эта модель является канонической., для этого вместо τ подставим его значение
Rx (t,t1 ) = D0 + ∑∞ Dk cos(kw(t −t1 )) , 2 k =1
но cos(kw(t-t1))=cos (kwt-kwt1)=cos(kwt) cos(kwt1)+sin(kwt) sin(kwt1),
тогда
Rx (t,t1 ) = D0 + ∑∞ Dk (cos(kwt) cos(kwt1 ) + sin(kwt)sin(kwt1 )) 2 k =1
Таким образом, сам сигнал может быть представлен в виде:
∞ |
∞ |
|
X (t) = Ф+ ∑U k cos kwt + ∑Vk sin kwt . |
(1.125) |
|
k =1 |
k =1 |
|
Коэффициенты разложения при этом обладают следующими свойствами.
1.M[Ф] = M[U k ] = M[Vk ] = 0 , то есть все они центрированы.
2.Коэффициенты разложения некоррелированны между собой: M[ФUk ] = M[ФVk ] = 0 при любых k.
0, k ≠ m
3.M[U kU m ] = Dk , k = m .
4.M[U kVm ] = 0
D[Ф] = D20 .
То есть сигнал описывается разложением:
60
