3 Расчет характеристик сигналов, передаваемых каналом связи

Исходные данные:

• методы цифровой модуляции №1 и №2;

• коэффициент ската спектра Найквиста ;

• длительность двоичного символа Т_б цифрового сигнала из задачи 2.

Необходимо:

• построить и описать схемы демодуляторов сигналов заданных методов модуляции;

• рассчитать и построить графики АЧХ ФНЧ 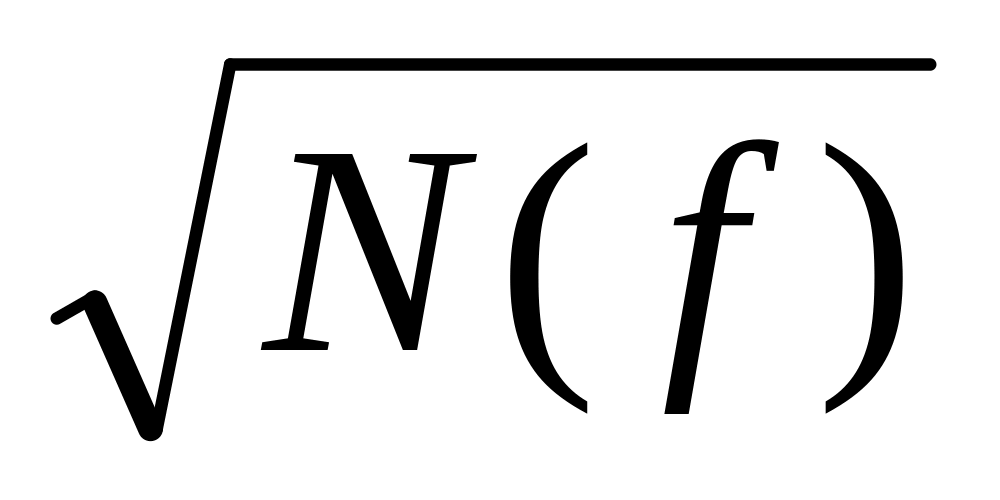и спектра Найквиста N(f) ;

• рассчитать пиковое отношение сигнал/шум на выходе СФ;

• рассчитать выигрыш в отношении сигнал/шум при фильтрации СФ;

• определить ширину спектра F_s, сравнить ее с шириной спектра F_max передаваемого непрерывного сигнала.

Теоретические сведения и расчетные соотношения

Для построения схемы демодулятора следует исходить из того, что сигнал цифровой модуляции – это последовательность канальных символов s_i(t). Символы следуют через тактовый интервал Т. Тактовый интервал определяется Т = Т_б log₂M где M – число позиций (уровней) модулированного сигнала. Схема демодулятора должна выполнять действия, предписанные аналитической записью канальных символов. Аналитические выражения для канальных символов s_i(t) и схемы оптимальных демодуляторов двумерных сигналов можно найти в [4, разд. 10], а для одномерных – в [4, разд. 9].

Формирующий и согласованный фильтры являются фильтрами нижних частот, но со специальной АЧХ. Если в качестве ФФ и СФ использовать фильтры Баттерворта, Чебышева и др., синтезированные с целью приближения их АЧХ к П-образной, то не будет выполняться условие отсутствия МСИ. Импульс на выходе СФ Р(t) должен удовлетворять условию отсутствия межсимвольной интерференции (МСИ), поэтому потребуем, чтобы спектр S_P(f) был спектром Найквиста N(f):

S_P(f) = N(f). (3.1)

Воспользуемся свойством СФ: его АЧХ совпадает с амплитудным спектром сигнала, с которым он согласован (при с = 1)

H_УФ(f) = S_A(f). (3.2)

Учитывая равенства (3.1) и (3.2) приходим к выводу, что

H_ФФ(f) = H_СФ(f) = . (3.3)

АЧХ ФФ и СФ описываются зависимостью «корень квадратный из спектра Найквиста». Аналитические выражения для N(f) и приведены в [4, разд. 5].

Рассчитать пиковое отношение сигнал/шум на выходе СФ демодулятора можно по формуле (4.9) из [4, разд. 4].

Рассчитать выигрыш в отношении сигнал/шум при фильтрации СФ демодулятора можно по формуле (4.10) из [4, разд. 4].

Ширина спектра модулированного сигнала определяется формулами, приведенными в [3, разд. 5.4, 5.5].

4 Анализ прохождения помехи через блоки демодулятора

Исходные данные:

• канал связи моделируется полосовым фильтром с П-образной АЧХ, полоса пропуска которого равна ширине спектра модулированного сигнала;

• в полосе пропускания канала связи действует аддитивный квазибелый гауссовский шум со спектральной плотностью мощности N₀;

• методы цифровой модуляции №1 и №2;

• минимальные расстояния между сигналами (Приложение Б);

• схемы демодуляторов из задачи 3.

Необходимо:

• выполнить анализ прохождения помехи через блоки демодулятора: синхронные детекторы, ФНЧ и решающее устройство;

• рассчитать и построить график условной плотности вероятности на одном из входов решающего устройства демодулятора двоичной модуляции;

• рассчитать вероятности ошибок сигнала модуляции №2 и сигнала модуляции №1;

• рассчитать вероятность ошибки двоичного символа в демодуляторе сигнала многопозиционной модуляции №1.

Теоретические сведения и расчетные соотношения

На вход демодулятора поступает помеха n(t) – аддитивный квазибелый гауссовский шум с равномерной спектральной плотностью мощности (СПМ) в полосе пропускания канала связи

(4.1)

Действие перемножителя на помеху можно определить, учитывая свойство преобразования Фурье: умножение на гармоническое колебание частоты f₀ порождает две составляющие, спектры которых сдвинуты на +f₀ и –f₀ относительно спектра входного сигнала. В этом случае СПМ каждой из двух составных получает множитель ¼. Если гармоническое колебание имеет амплитуду , то множитель равняется ¼( )² = ½. Каждая из составляющих также является белым шумом, а сами составляющие независимы на любой из частот. Поэтому СПМ их суммы в интервале частот (–F_s/2 < f <F_s/2) вдвое больше СПМ каждой из них, и, таким образом, на выходах каждого из перемножителей имеет место квазибелый шум с СПМ

(4.2)

Мощность шума на выходе ФНЧ легко определить, если известная его шумовая полоса F_ш.

С выхода ФНЧ берется отсчет помехи, и имеем  – случайную величину с гауссовским распределением вероятности. Ее дисперсия (мощность) равняется дисперсии помехи на выходе ФНЧ

(4.3)

Итак, на основе анализа прохождения сигнала и помехи через блоки демодулятора на входах решающего устройства имеем оценки координат переданного сигнала = a_iс + _c и = a_is + _s, где а_іс, a_is – числа, которые описывают переданный сигнал; _с, _s – независимые отсчеты помех в подканалах демодулятора со среднеквадратическим отклонением (СКО) . Условную плотность вероятности на косинусном входе решающего устройства при условии, что передавался сигнал s₀, можно записать [4, разд. 11, разд. 12]

(4.4)

Алгоритм работы решающего устройства следующий. Вся плоскость, на которую нанесено сигнальное созвездие, разбивается на М непересекающихся областей. Границами областей должны быть совокупности точек, находящихся на равных расстояниях от ближайших сигнальных точек – это минимизирует вероятность ошибки при вынесении решения о номере переданного сигнала.

Знание сигнального созвездия и СКО помехи достаточно для расчета вероятности ошибки сигнала. Ошибка сигнала некоторого сигнала будет иметь место, если хотя бы одна из координат попадет в область другого сигнала. Поэтому условием возникновения ошибки является _с > d/2 или _s > d/2, а вероятность ошибки [4, разд. 12]

(4.5)

где m – количество ошибочных переходов: для ФМ-4 m = 2, для КАМ-8 m = 3, для КАМ-16 m = 4, если учесть лишь переходы в ближайшие сигналы;

F_(х) – функция распределения вероятности случайной величины ;

Q(z) – интеграл вероятности;

 – это _с или _s.

Так просто формулируется условие возникновения ошибок, когда линии, соединяющие сигнальные точки, параллельны оси а_c или оси a_s. Если линия, которая соединяет сигнальные точки, не параллельна ни одной из осей координат, то условие возникновения ошибки формулируется по-иному. Такая ситуация имеет место в случае ФМ-8. Анализ показывает, что в случае ФМ-8 вероятность ошибки сигнала определяется формулой (4.5), m = 2.

Если используется модуляционный код Грея, то в случае ошибки сигнала возникает ошибка лишь в одном разряде комбинации, которая передается этим сигналом. В таком случае вероятность ошибки двоичного символа (бита) определяется

р = Р_ош/n, (4.6)

где n определяется соотношением .

Рекомендованный порядок выполнения задачи 4

Описать преобразование помехи в демодуляторе.

Рассчитать значения дисперсий на входах решающего устройства – формула (4.3).

Рассчитать и построить график условной плотности вероятности на одном из входов решающего устройства при условии, что передавался некоторый канальный символ – формула (4.4): дисперсия рассчитана выше, а координаты произвольно выбранного канального символа.

Рассчитать вероятности ошибок сигнала и двоичного символа по формулам (4.6), (4.5).